Giải SBT Toán 11 bài 1: Đại cương về đường thẳng và mặt phẳng

Toán 11 - Đại cương về đường thẳng và mặt phẳng

VnDoc xin giới thiệu tới thầy cô và các bạn học sinh tài liệu Giải SBT Toán 11 bài 1: Đại cương về đường thẳng và mặt phẳng, với nội dung được tổng hợp và đăng tải chi tiết, chính xác sẽ giúp các bạn học sinh có kết quả cao hơn trong học tập.

Giải SBT Toán 11 bài 1

Bài 2.1 trang 66 Sách bài tập (SBT) Hình học 11

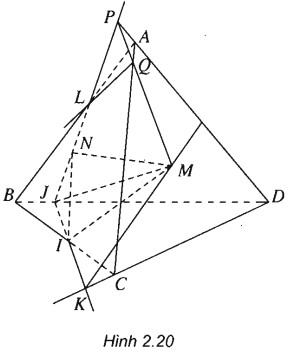
Cho tứ diện ABCD và điểm M thuộc miền trong của tam giác ACD. Gọi I và J tương ứng là hai điểm trên cạnh BC và BD sao cho IJ không song song với CD

a) Hãy xác định giao tuyến của hai mặt phẳng (IJM) và (ACD).

b) Lấy N là điểm thuộc miền trong của tam giác ABD sao cho JN cắt đoạn AB tại L. Tìm giao tuyến của hai mặt phẳng (MNJ) và (ABC)

Giải:

(h.2.20)

a) Nhận xét:

Do giả thiết cho IJ không song song với CD và chúng cùng nằm trong mặt phẳng (BCD) nên khi kéo dài chúng gặp nhau tại một điểm.

Gọi K=IJ∩CD

Ta có: M là điểm chung thứ nhất của (ACD) và (IJM);

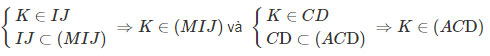
Vậy (MIJ)∩(ACD)=MK

b) Với L=JN∩AB ta có:

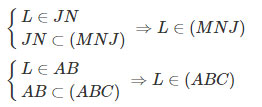
Như vậy L là điểm chung thứ nhất của hai mặt phẳng (MNJ) và (ABC)

Gọi P=JL∩AD, Q=PM∩AC

Ta có:

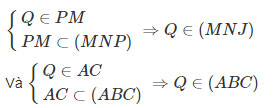
Nên Q là điểm chung thứ hai của (MNJ) và (ABC)

Vậy LQ=(ABC)∩(MNJ)

Bài 2.2 trang 66 Sách bài tập (SBT) Hình học 11

Cho hình chóp S.ABCDcó đáy là tứ giác ABCD có hai cạnh đối diện không song song. Lấy điểm M thuộc miền trong của tam giác SCD.

Tìm giao tuyến của hai mặt phẳng

a) (SBM) và (SCD);

b) (ABM) và (SCD);

c) (ABM) và (SAC).

Giải:

(h.2.21)

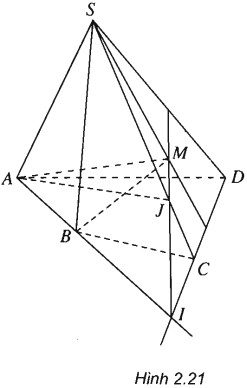
a) Ta có ngay S, M là hai điểm chung của (SBM) và (SCD) nên (SBM)∩(SCD)=SM

b) M là điểm chung thứ nhất của (AMB) và (SCD)

Gọi I=AB∩CD

Ta có: I∈AB⇒I∈(ABM)

Mặt khác I∈CD⇒I∈(SCD)

Nên (AMB)∩(SCD)=IM

c) Gọi J=IM∩SC

Tacó: J∈SC⇒J∈(SAC) và J∈IM⇒J∈(ABM)

Hiển nhiên A∈(SAC) và A∈(ABM)

Vậy (SAC)∩(ABM)=AJ

Bài 2.3 trang 66 Sách bài tập (SBT) Hình học 11

Cho tứ diện ABCD. Trên cạnh AB lấy điểm I và lấy các điểm J, K lần lượt là điểm thuộc miền trong các tam giác BCD và ACD. Gọi L là giao điểm của JK với mặt phẳng (ABC)

a) Hãy xác định điểm L.

b) Tìm giao tuyến của mặt phẳng (IJK) với các mặt của tứ diện ABCD.

Giải:

(h.2.22)

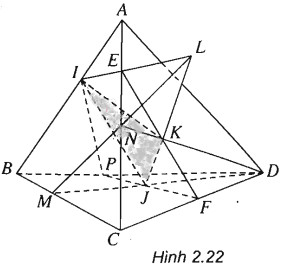
a) Gọi N=DK∩AC;M=DJ∩BC

Ta có (DJK)∩(ABC)=MN⇒MN⊂(ABC)

Vì L=(ABC)∩JK nên dễ thấy L=JK∩MN

b) Ta có I là một điểm chung của (ABC) và (IJK).

Mặt khác vì L=MN∩JK mà MN⊂(ABC) và JK⊂(IJK) nên L là điểm chung thứ hai của (ABC) và (IJK), suy ra (IJK)∩(ABC)=IL.

Gọi E=IL∩AC;F=EK∩CD. Lí luận tương tự ta có EF=(IJK)∩(ACD)

Nối FJ cắt BD tại P; P là một giao điểm (IJK) và (BCD).

Ta có PF=(IJK)∩(BCD)

Và IP=(ABD)∩(IJK)

Bài 2.4 trang 66 Sách bài tập (SBT) Hình học 11

Cho tứ diện ABCD có các điểm M và N lần lượt là trung điểm của AC và BC. Lấy điểm K thuộc đoạn BD (K không là trung điểm của BD). Tìm giao điểm của đường thẳng AD và mặt phẳng (MNK).

Giải:

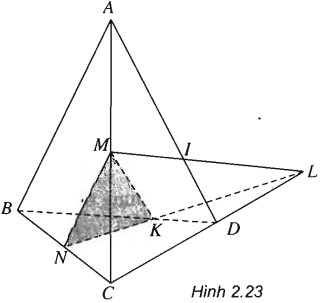
Nhận xét. Trên hình vẽ 2.23 không có sẵn đường thẳng nào của mặt phẳng (MNK) cắt AD. Ta xét mặt phẳng chứa AD chẳng hạn (ACD) rồi tìm giao tuyến ∆ của (ACD) với (MNK). Sau đó tìm giao điểm I của ∆ và AD, I chính là giao điểm phải tìm.

Gọi L=NK∩CD

Ta có L∈NK⇒L∈(MNK)

L∈CD⇒L∈(ACD)

Nên ML=(ACD)∩(MNK)=Δ

Δ∩AD=I⇒I=(MNK)∩AD

Bài 2.5 trang 67 Sách bài tập (SBT) Hình học 11

Cho hình chóp S. ABCD. Lấy M, N và P lần lượt là các điểm trên các đoạn SA, AB và BC sao cho chúng không trùng với trung điểm của các đoạn thẳng ấy. Tìm giao điểm (nếu có) của mặt phẳng (MNP) với các cạnh của hình chóp.

Giải:

(h.2.24)

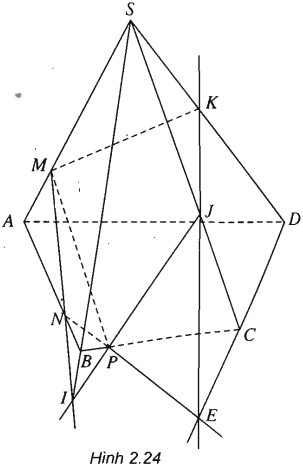
Ta lần lượt tìm giao điểm của mặt phẳng (MNP) với các đường thẳng chứa các cạnh của hình chóp.

Gọi I=MN∩SB

Ta có:

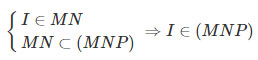
Vậy I=SB∩(MNP).

Từ đó, làm tương tự ta tìm được giao điểm của (MNP) với các cạnh còn lại.

Cụ thể :

Gọi J=IP∩SC, ta có J=SC∩(MNP)

Gọi E=NP∩CD, ta có E=CD∩(MNP)

Gọi K=JE∩SD, ta có K=SD∩(MNP)

Bài 2.6 trang 67 Sách bài tập (SBT) Hình học 11

Cho hình chóp S.ABCD. M và N tương ứng là các điểm thuộc các cạnh SC và BC. Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN).

Giải:

(h.2.25)

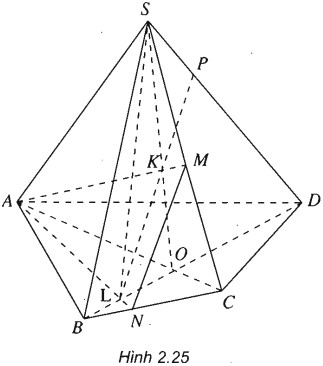
Gọi

O=AC∩BD

K=SO∩AN

L=BD∩AN

P=KL∩SD

Ta có P=SD∩(AMN)

Nhận xét. Trong cách giải trên, ta lấy (SBD) là mặt phẳng chứa SD, rồi tìm giao tuyến của (SBD) với (AMN). Từ đó tìm giao điểm của giao tuyến này và SD.

Bài 2.7 trang 67 Sách bài tập (SBT) Hình học 11

Cho tứ diện SABC. Trên SA, SB và SC lần lượt lấy các điểm D, E và F sao cho DE cắt AB tại I, EF cắt BC tại J, FD cắt CA tại K.

Chứng minh ba điểm I, J, K thẳng hàng.

Giải:

(h.2.26)

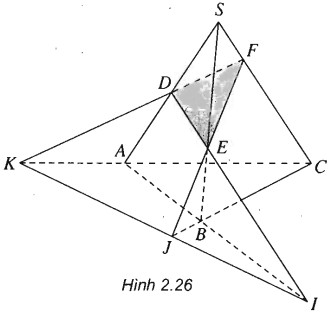
Ta có:

I=DE∩AB

DE⊂(DEF)⇒I∈(DEF)

AB⊂(ABC)⇒I∈(ABC)

Lí luận tương tự thì J, K cũng lần lượt thuộc về hai mặt phẳng trên nên I, J, K thuộc về giao tuyến của (ABC) và (DEF) nên I, J, K thẳng hàng.

Bài 2.8 trang 67 Sách bài tập (SBT) Hình học 11

Cho hai mặt phẳng (α) và ((β) cắt nhau theo giao tuyến d. Trong (α) lấy hai điểm A và B sao cho AB cắt d tại I. O là một điểm nằm ngoài (α) và (β) sao cho OA và OB lần lượt cắt (β) tại A’ và B’.

a) Chứng minh ba điểm I, A’, B’ thẳng hàng.

b) Trong (α) lấy điểm C sao cho A, B, C không thẳng hàng. Giả sử OC cắt (β) tại C’, BC cắt B’C’ tại J, CA cắt C’A’ tại K. Chứng minh I, J, K thẳng hàng.

Giải:

(h.2.27)

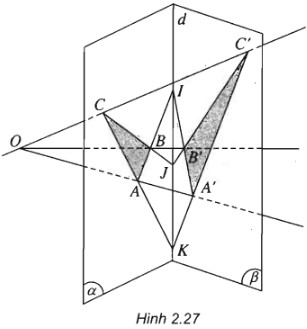
a) I, A’, B’ là ba điểm chung của hai mặt phẳng (OAB) và (β) nên chúng thẳng hàng.

b) I, J, K là ba điểm chung của hai mặt phẳng (ABC) và (A’B’C’) nên chúng thẳng hàng.

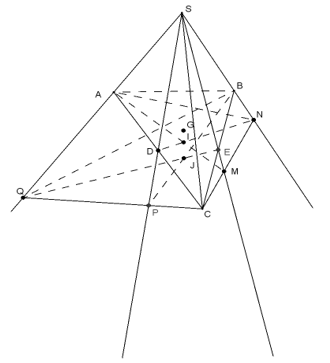
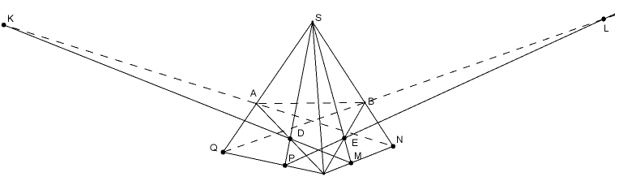
Bài 2.9 trang 67 Sách bài tập (SBT) Hình học 11

Cho tứ diện S.ABC có D, E lần lượt trung điểm AC, BC và G là trọng tâm tam giác ABC. Mặt phẳng (α) (α) qua AC cắt SE, SB lần lượt tại M, N. Một mặt phẳng (β) qua BC cắt SD và SA lần lượt tại P và Q.

a) Gọi I=AM∩DN,J=BP∩EQ. Chứng minh bốn điểm S, I, J, G thẳng hàng.

b) Giả sử AN∩DM=K,BQ∩EP=L. Chứng minh ba điểm S, K, L thẳng hàng.

Giải:

a) Ta thấy:

+ G là trọng tâm tam giác ABC ⇒G∈BD

+ I∈DN (theo cách dựng hình).

+ J∈BP (theo cách dựng hình).

⇒S,I,J,G∈mp(SPN)

Tương tự ⇒S,I,J,G∈mp(SQM)

Vậy S,I,J,G là điểm chung của mp(SPN) và mp(SQM)

Ta thấy:

+ S=PD∩EM

+ K∈DM

+ L∈PE

⇒S,K,L∈(SPM)

Tương tự ⇒S,K,L∈(SQN)

Vậy S,K,L là điểm chung của (SPM) và (SQN)

-----------------------------------

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải SBT Toán 11 bài 1: Đại cương về đường thẳng và mặt phẳng. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Sinh học lớp 11, Vật lý lớp 11, Hóa học lớp 11, Giải bài tập Toán 11 mà VnDoc tổng hợp và đăng tải.