Giải SBT Toán 11 bài 4: Cấp số nhân
Toán 11 - Cấp số nhân
VnDoc xin giới thiệu tới các bạn học sinh lớp 11 tài liệu Giải SBT Toán 11 bài 4: Cấp số nhân, nội dung kèm theo lời giải chi tiết sẽ là nguồn thông tin hay để phục vụ công việc học tập của các bạn học sinh được tốt hơn.
Giải SBT Toán 11 ôn tập chương 2: Tổ hợp - Xác suất
Giải SBT Toán 11 bài 1: Phương pháp quy nạp toán học
Giải SBT Toán 11 bài 4
Bài 4.1 trang 125 Sách bài tập (SBT) Đại số 11 và giải tích 11
Cho dãy số (un) với un=(−3)2n−1
a) Chứng minh dãy số (un) là cấp số nhân. Nêu nhận xét về tính tăng, giảm của dãy số;
b) Lập công thức truy hồi của dãy số;
c) Hỏi số là số hạng thứ mấy của dãy số?
Giải:
a) Có thể lập tỉ số un+1/un. Cấp số nhân có u1=−3,q=9
Xét hiệu
H=un+1−un
=(−3)2n+1−(−3)2n−1
=(−3)2n[(−3)1−(−3)−1]
=9n(−8/3)<0
vậy dãy số giảm.
b) Công thức truy hồi
{u1=−3;un+1=9.un với n≥1
c) Số hạng thứ năm.
Bài 4.2 trang 125 Sách bài tập (SBT) Đại số và giải tích 11
Cấp số nhân 
\($\left( {{u_n}} \right)$\) có
{u1+u5=51;u2+u6=102
a) Tìm số hạng đầu và công bội của cấp số nhân:
b) Hỏi tổng của bao nhiêu số hạng đầu tiên sẽ bằng 3096?
c) Số 12 288 là số hạng thứ mấy?
Giải
ĐS:
a) u1=3,q=2
b) n = 10
c) n = 13
Bài 4.3 trang 125 Sách bài tập (SBT) Đại số và giải tích 11
Tìm số các số hạng của cấp số nhân (un) biết
a) q=2,un=96,Sn=189;
b) u1=2,un=1/8,Sn=31/8
Giải:
ĐS:
a) n = 6
b) n = 5
Bài 4.4 trang 125 Sách bài tập (SBT) Đại số và giải tích 11
Tìm số hạng đầu và công bội của cấp số nhân (un) biết
a)
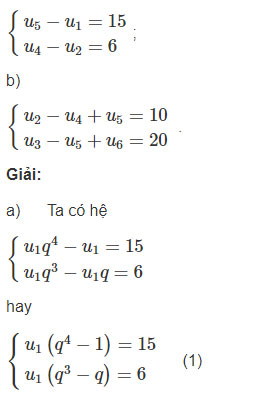
Do (1) nên q≠±1 suy ra 15/6=q4−1/q(q2−1)=q2+1/q
Biến đổi về phương trình 2q2−5q+2=0
Giải ra được q = 2 và q=1/2
Nếu q = 2 thì u1 = 1
Nếu q=1/2 thì u1 = -16
b) ĐS: u1=1,q=2
Bài 4.5 trang 126 Sách bài tập (SBT) Đại số và giải tích 11
Bốn số lập thành một cấp số cộng. Lần lượt trừ mỗi số ấy cho 2, 6, 7, 2 ta nhận được một cấp số nhân. Tìm các số đó.
Giải:
HD: Gọi 4 số cần tìm là x,y,z,t ta có:
Cấp số cộng x,y,z,t
Cấp số nhân x−2,y−6,z−7,t−2
Ta có hệ
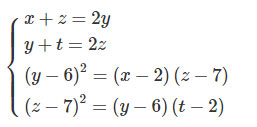
ĐS: x=5,y=12,z=19,t=26
Bài 4.6 trang 126 Sách bài tập (SBT) Đại số và giải tích 11
Viết bốn số xen giữa các số 5 và 160 để được một cấp số nhân.
Giải:
ĐS: 10, 20, 40, 80
Bài 4.7 trang 126 Sách bài tập (SBT) Đại số và giải tích 11
Cho dãy số
(un):{u1=0;un+1=2un+3/un+4 với n≥1
a) Lập dãy số (xn) với xn=un−1/un+3. Chứng minh dãy số là cấp số nhân.
b) Tìm công thức tính xn,un theo n.
Giải:
Từ giả thiết có
un+1(un+4)=2un+3 hay \(\({u_{n + 1}}.{u_n} + 4{u_{n + 1}} = 2{u_n} + 3)\) (1)
Lập tỉ số
xn+1/xn=un+1−1/un+1+3.un+3/un−1=un+1un+3un+1−un−3/un+1un−un+1+3un−3 (2)
Từ (1) suy ra un+1.un=2un+3−4un+1 thay vào (2) ta được
xn+1/xn=2un+3−4un+1+3un+1−un−3/2un+3−4un+1−un+1+3un−3=un−un+1/5(un−un+1)=1/5
Vậy xn+1=1/5xn ta có cấp số nhân (xn) với q=1/5 và x1=−1/3
Ta có xn=−1/3(1/5)n−1
Từ đó tìm được un=3xn−1/1−xn
\(=\frac{-\left(\frac{1}{5}\right)^{n-1}-1}{1+\frac{1}{3}\left(\frac{1}{5}\right)^{n-1}}=\frac{\left(\frac{1}{5}\right)^{n-1}+1}{\frac{1}{3}\left(\frac{1}{5}\right)^{n-1}+1}\)
Bài 4.8 trang 126 Sách bài tập (SBT) Đại số và giải tích 11
Ba số khác nhau có tổng bằng 114 có thể coi là ba số hạng liên tiếp của một cấp số nhân, hoặc coi là các số hạng thứ nhất, thứ tư và thứ hai mươi lăm của một cấp số cộng. Tìm các số đó.
Giải:
HD: làm tương tự ví dụ 7/12 Bài 4.
ĐS: Ba số phải tìm là 2, 14, 98
Bài 4.9 trang 126 Sách bài tập (SBT) Đại số và giải tích 11
Cho cấp số nhân,a, b, c, d. Chứng minh rằng
a) a2b2c2(1/a3+1/b3+1/c3)=a3+b3+c3;
b) (ab+bc+cd)2=(a2+b2+c2)(b2+c2+d2)
Giải:
a) Biến đổi vế trái
a2b2c2(1/a3+1/b3+1/c3)
=b2c2/a+a2c2/b+a2b2/c
=acc2/a+(b2)2/b+a2ac/c
=a3+b3+c3
b) HD: Áp dụng bất đẳng thức Bu-nhi-a-cốp-xki cho các số a, b, c và b, c, d.
Bài 4.10 trang 126 Sách bài tập (SBT) Đại số và giải tích 11
Giải phương trình ax3+bx2+cx+d=0 biết a, b, c, d là một cấp số nhân với công bội q.
Giải:
HD: Thay các hệ số a, b, c, d lần lượt bằng a,aq,aq2,aq3 vào phương trình và biến đổi
-----------------------------------
Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải SBT Toán 11 bài 4: Cấp số nhân. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Sinh học lớp 11, Vật lý lớp 11, Hóa học lớp 11, Giải bài tập Toán 11 mà VnDoc tổng hợp và đăng tải.
