Giải SBT Toán 11 bài 2: Giới hạn của hàm số
Toán 11 - Giới hạn của hàm số
VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải SBT Toán 11 bài 2: Giới hạn của hàm số, hy vọng qua bộ tài liệu các bạn học sinh sẽ có kết quả cao hơn trong học tập.
Giải SBT Toán 11 bài 3: Cấp số cộng
Giải SBT Toán 11 bài 4: Cấp số nhân
Giải SBT Toán 11 ôn tập chương 3: Dãy số. Cấp số cộng và cấp số nhân
Giới hạn của hàm số
Bài 2.1 trang 163 Sách bài tập (SBT) Đại số và giải tích 11
Dùng định nghĩa tìm các giới hạn
a) limx→5x+3/x−3
b) limx→+∞x3+1/x2+1
Giải:
a) - 4 ; b) + ∞
Bài 2.3 trang 163 Sách bài tập (SBT) Đại số và giải tích 11
a) Chứng minh rằng hàm số y=sinx không có giới hạn khi x→+∞
b) Giải thích bằng đồ thị kết luận ở câu a).
Giải:
a) Xét hai dãy số (an) với an=2nπ và (bn) với (bn)=π/2+2nπ(n∈N∗)
Ta có, liman=lim2nπ=+∞
limbn=lim(π/2+2nπ)
=limn(π/2n+2π)=+∞
limsinan=limsin2nπ=lim0=0
limsinbn=limsin(π/2+2nπ)=lim1=1
Như vậy, an→+∞,bn→+∞ nhưng limsinan≠limsinbn. Do đó, theo định nghĩa, hàm số y=sinx không có giới hạn khi x→+∞
Bài 2.4 trang 163 Sách bài tập (SBT) Đại số và giải tích 11
Cho hai hàm số y=f(x) và y=g(x) cùng xác định trên khoảng (−∞,a). Dùng định nghĩa chứng minh rằng, nếu limx→−∞f(x)=L và limx→−∞g(x)=M thì limx→−∞f(x).g(x)=L.M
Giải:
Giả sử (xn) là dãy số bất kì thoả mãn xn<ax và xn→−∞
Vì limx→−∞f(x)=L nên limn→+∞f(xn)=L
Vì limx→−∞g(x)=M nên limn→+∞g(xn)=M
Do đó, limn→+∞f(xn).g(xn)=L.M
Từ định nghĩa suy ra limx→−∞f(x).g(x)=L.M
Bài 2.5 trang 163 Sách bài tập (SBT) Đại số và giải tích 11
Tìm giới hạn của các hàm số sau:
a) f(x)=x2−2x−3/x−1 khi x→3;
b) h(x)=2x3+15/(x+2)2 khi x→−2;
c) k(x)=
\(\sqrt{4x^2-x+1}\) khi x→−∞;
d) f(x)=x3+x2+1 khi x→−∞
e) h(x)=x−15/x+2 khi x→−2+ và khi x→−2−
Giải:
a) 0;
b) −∞;
c) limx→−∞\(\sqrt{4x^2-x+1}\)
=limx→−∞|x|\(\sqrt{4-\frac{1}{x}+\frac{1}{x^2}}\)
=limx→−∞\(\left(-x\sqrt{4-\frac{1}{x}+\frac{1}{x^2}}\right)\)=+∞
d) limx→−∞(x3+x2+1)=limx→−∞x3(1+1/x+1/x3)=−∞
e) −∞ và +∞
Bài 2.6 trang 163 Sách bài tập (SBT) Đại số 11 và giải tích 11
Tính các giới hạn sau:
a) limx→−3x+3/x2+2x−3
b) limx→0(1+x)3−1/x
c) limx→+∞x−1/x2−1
d) limx→5x−5/√x−√5
e) limx→+∞=x−5/√x+√5
f) limx→−2√x2+5−3/x+2
g) limx→1√x−1/√x+3−2
h) limx→+∞1−2x+3x3/x3−9
i) limx→01/x2.(1/x2+1.−1)
j) limx→−∞(x2−1)(1−2x)5/x7+x+3
Giải:
a) limx→−3x+3/x2+2x−3=limx→−3x+3/(x−1)(x+3)=limx→−31/x−1=−1/4
b)
limx→0(1+x)3−1/x
=limx→0(1+x−1)[(1+x)2+(1+x)+1]/x
=limx→0x[(1+x)2+(1+x)+1]/x
=limx→0[(1+x)2+(1+x)+1]=3
c) limx→+∞x−1/x2−1=limx→+∞\(\frac{\frac{1}{x}-\frac{1}{x^2}}{1-\frac{1}{x^2}}=0\)
d) limx→5x−5/√x−√5
=limx→5(√x−√5)(√x+√5)/√x−√5
=limx→5(√x+√5)=2√5
e)
limx→+∞x−5/√x+√5
=limx→+∞\(\frac{1-\frac{5}{x}}{\frac{1}{\sqrt{x}}+\frac{\sqrt{5}}{x}}\)=+∞
(Vì 1/√x+√5/x>0 với mọi x>0).
f) limx→−2√x2+5−3/x+2
=limx→−2x2+5−9/(x+2)(√x2+5+3)
=limx→−2(x−2)(x+2)/(x+2)(√x2+5+3)
=limx→−2x−2/√x2+5+3=−2/3
g)
limx→1√x−1/√x+3−2
=limx→1(√x−1)(√x+3+2)/x+3−4
=limx→1(√x−1)(√x+3+2)/x−1
=limx→1(√x−1)(√x+3+2)/(√x−1)(√x+1)
=limx→1√x+3+2/√x+1=2
h) limx→+∞1−2x+3x3/x3−9=limx→+∞\(\frac{\frac{1}{x^3}-\frac{2}{x^2}+3}{1-\frac{9}{x^3}}=3\)
i)
limx→01/x2(1/x2+1−1)
=limx→01/x2.(−x2/x2+1)
=limx→0−1/x2+1=−1
j)
limx→−∞(x2−1)(1−2x)5/x7+x+3
=limx→−∞x2(1−1/x2).x5(1/x−2)5/x7+x+3
=limx→−∞(1−1/x2)(1/x−2)5/1+1/x6+3/x7
=(−2)5=−32
Bài 2.7 trang 164 Sách bài tập (SBT) Đại số và giải tích 11
Tính giới hạn của các hàm số sau khi x→+∞ và khi x→−∞
a) f(x)=\(\frac{\sqrt{x^2-3x}}{x+2}\)
b) f(x)=x+\(\sqrt{x^2-x+1}\)
c) f(x)=\(\sqrt{x^2-x}-\sqrt{x^2+1}\)
Giải:
a) Khi x→+∞
limx→+∞\(\frac{\sqrt{x^2-3x}}{x+2}\)=limx→+∞\(\frac{|x|\sqrt{1-3x}}{x+2}\)
=limx→+∞\(\frac{x\sqrt{1-\frac{3}{x}}}{x+2}\)=limx→+∞\(\frac{\sqrt{1-\frac{3}{x}}}{1+\frac{2}{x}}=1\)
Khi x→−∞
x→−∞\(\sqrt{x^2-3x}\)/x+2=limx→−∞|x|\(\sqrt{1-\frac{3}{x}}\)/x+2
=limx→−∞−x\(\sqrt{1-\frac{3}{x}}\)/x+2=limx→−∞\(-\sqrt{\frac{1-\frac{3}{x}}{1+\frac{2}{x}}}=-1\)
b) Khi x→+∞
limx→+∞(x+\(\sqrt{x^2-x+1}\))
=limx→+∞\(\left(x+x\sqrt{1-\frac{1}{x}+\frac{1}{x^2}}\right)\)
=limx→+∞x\(\left(1+\sqrt{1-\frac{1}{x}+\frac{1}{x^2}}\right)\)=+∞
Khi x→−∞
limx→−∞(x+\(\sqrt{x^2-x+1}\))
=limx→−∞\(\frac{x^2-(x^2-1+1)}{x-\sqrt{x^2-x+1}}\)
=limx→−∞\(\frac{x-1}{x-\sqrt{x^2-x+1}}\)
=limx→−∞\(\frac{x-1}{x-|x|\sqrt{1-\frac{1}{x}+\frac{1}{x^2}}}\)
=limx→−∞\(\frac{x-1}{x+x\sqrt{1-\frac{1}{x}+\frac{1}{x^2}}}\)
=limx→−∞\(\frac{1-\frac{1}{x}}{1+\sqrt{1-\frac{1}{x}+\frac{1}{x^2}}}\)
c) Khi x→+∞
limx→+∞(\(\sqrt{x^2-x}-\sqrt{x^2+1}\))
=limx→+∞\(\frac{(x^2-x)-(x^2+1)}{\sqrt{x^2-x}+\sqrt{x^2+1}}\)
=limx→+∞\(\frac{-x-1}{x\sqrt{1-\frac{1}{x}+x}\sqrt{1+\frac{1}{x^2}}}\)
=limx→+∞\(\frac{-1-\frac{1}{x}}{\sqrt{1-\frac{1}{x}}+1+\frac{1}{x^2}}=\frac{-1}{2}\)
Khi x→−∞
limx→−∞\(\left(\sqrt{x^2-x}-\sqrt{x^2+1}\right)\)
=limx→−∞\(\frac{\left(x^2-x\right)-\left(x^2+1\right)}{\sqrt{x^2-x}+\sqrt{x^2+1}}\)
=limx→−∞\(\frac{-x-1}{-x\sqrt{1-\frac{1}{x}-x\sqrt{1+\frac{1}{x^2}}}}\)
=limx→−∞\(\frac{-1-\frac{1}{x}}{-\sqrt{1-\frac{1}{x^{ }}}-\sqrt{1+\frac{1}{x^2}}}=\frac{1}{2}\)
Bài 2.8 trang 164 Sách bài tập (SBT) Đại số và giải tích 11
Cho hàm số f(x)=2x2−15x+12/x2−5x+4 có đồ thị như hình 4
a) Dựa vào đồ thị, dự đoán giới hạn của hàm f(x) số khi x→1+;x→1−;x→4+;x→4−;x→+∞;x→−∞
b) Chứng minh dự đoán trên.
Giải:
a) Dự đoán:
limx→1+f(x)=+∞;limx→1−f(x)=−∞;limx→4+f(x)=−∞;
limx→4−f(x)=+∞;limx→+∞f(x)=2;limx→−∞f(x)=2.
b) Ta có
limx→1+(2x2−15x+12)=−1<0,limx→1+(x2−5x+4)=0
và x2−5x+4<0 với mọi x∈(1;4) nên limx→1+2x2−15x+12/x2−5x+4=+∞
Vì
limx→1−(2x2−15x+12)=−1<0,
limx→1−(x2−5x+4)=0
và x2−5x+4>0 với mọi x < 1 nên limx→1−2x2−15x+12/x2−5x+4=−∞
Vì
limx→4+(2x2−15x+12)=−16<0,
limx→4+(x2−5x+4)=0
và x2−5x+4>0 với mọi x > 4 nên limx→4+2x2−15x+12/x2−5x+4=−∞
Vì
limx→4−(2x2−15x+12)=−16<0,
limx→4−(x2−5x+4)=0
và x2−5x+4<0 với mọi x∈(1;4) nên limx→4−2x2−15x+12/x2−5x+4=+∞
limx→+∞2x2−15x+12/x2−5x+4=limx→+∞ \(\frac{2-\frac{15}{x}+\frac{12}{x^2}}{1-\frac{5}{x}+\frac{4}{x^2}}=2\)
limx→−∞2x2−15x+12/x2−5x+4=limx→−∞\(\frac{2-\frac{15}{x}+\frac{12}{x^2}}{1-\frac{5}{x}+\frac{4}{x^2}}=2\)
Bài 2.9 trang 164 Sách bài tập (SBT) Đại số và giải tích 11
Cho hàm số
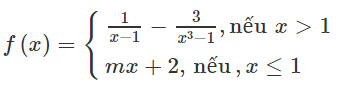
Với giá trị nào của tham số m thì hàm số f(x) có giới hạn khi x→1? Tìm giới hạn này.
Giải:
limx→1+f(x)=limx→1+(1/x−1−3/x3−1)
=limx→1+x2+x−2/(x−1)(x2+x+1)
=limx→1+(x−1)(x+2)/(x−1)(x2+x+1)
=limx→1+x+2/x2+x+1=1
limx→1−f(x)=limx→1−(mx+2)=m+2
f(x) có giới hạn khi x→1⇔m+2=1⇔m=−1. Khi đó limx→1f(x)=1
Bài 2.10 trang 164 Sách bài tập (SBT) Đại số và giải tích 11
Cho khoảng K,x0∈K và hàm số y=f(x) xác định trên K∖{x0}
Chứng minh rằng nếu limx→x0f(x)=+∞ thì luôn tồn tại ít nhất một số c thuộc K∖{x0} sao cho f(c)>0
Giải:
Vì limx→x0f(x)=+∞ nên với dãy số (xn) bất kì, xn∈K∖{x0} và xn→x0 ta luôn có limn→+∞f(xn)=+∞
Từ định nghĩa suy ra f(xn) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Nếu số dương này là 1 thì f(xn)>1 kể từ một số hạng nào đó trởđi.
Nói cách khác, luôn tồn tạiít nhất một số xk∈K∖{xo} sao cho f(xk)>1.
Đặt c=xk ta có f(c)>0
Bài 2.11 trang 165 Sách bài tập (SBT) Đại số và giải tích
Cho hàm số \($y = f\left( x \right)$\) xác định trên khoảng (a;+∞)
Chứng minh rằng nếu limx→+∞f(x)=−∞ thì luôn tồn tại ít nhất một sốc thuộc (a;+∞) sao cho f(c)<0
Giải:
Vì limx→+∞f(x)=−∞ nên với dãy số (xn) bất kì, xn>a và xn→+∞ ta luôn có limn→+∞f(x)=−∞
Do đó limn→+∞[−f(xn)]=+∞
Theo định nghĩa suy ra −f(xn) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Nếu số dương này là 2 thì −f(xn)>2 kể từ một số hạng nàođó trởđi.
Nói cách khác, luôn tồn tại ít nhất một số xk∈(a;+∞) sao cho −f(xk)>2 hay f(xk)<−2<0
Đặt c=xk ta có f(c)<0
-----------------------------------
Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải SBT Toán 11 bài 2: Giới hạn của hàm số. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Sinh học lớp 11, Vật lý lớp 11, Hóa học lớp 11, Giải bài tập Toán 11 mà VnDoc tổng hợp và đăng tải.
