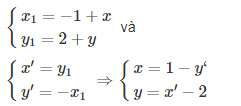Giải SBT Toán 11 đề kiểm tra chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng

Toán 11 - Phép dời hình và phép đồng dạng trong mặt phẳng

Để giúp các bạn học sinh rèn luyện giải bài tập Toán 11 nhanh và hiệu quả, VnDoc mời các bạn tham khảo tài liệu Giải SBT Toán 11 đề kiểm tra chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng, nội dung được tổng hợp chi tiết và chính xác sẽ giúp các bạn học sinh có kết quả cao hơn trong học tập.

Giải SBT Toán 11 đề kiểm tra chương 1

Đề 1 trang 41 Sách bài tập (SBT) Hình học 11

Câu 1. (5 điểm )

Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x−y−3=0. Viết phương trình đường thẳng d₁ là ảnh của d qua phép dời hình có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ v^→=(−1;2) và phép quay tâm O góc quay -90°.

Câu 2. (5 điểm )

Trong mặt phẳng Oxy cho đường tròn (x−1)²+(y−2)²=9. Viết phương trình đường tròn ảnh của đường tròn đã cho qua phép dời hình có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ v^→=(2;0) phép vị tự tâm O tỉ số k=−3.

Giải:

Câu 1.

Lấy điểm M=(x;y)

Giả sử M₁=T_v^→(M) và M′=Q_(O,−90⁰)(M₁)

Ta có:

Thế (x;y) theo (x′;y′) vào phương trình, ta có:

3(1−y′)−(x′−2)−3=0. Như vậy phương trình d’ là:

x′+3y′−2=0 hay x+3y−2=0x+3

Câu 2. Cách 1.

Giả sử M₁=T_v^→(M) và M′=V_(O,k=−3)(M₁). Ta có:

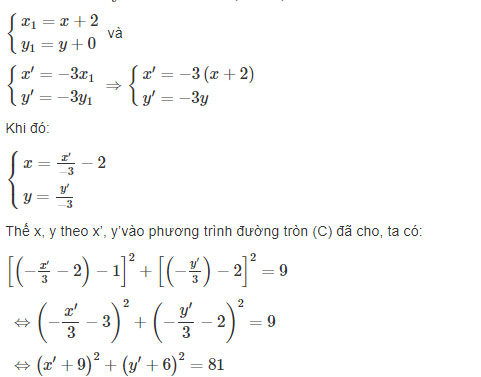
Vậy (x+9)²+(y+6)²=81 là phương trình của đường tròn ảnh (C’) của đường tròn (C) qua phép dời hình đã cho.

Cách 2.

Đường tròn (C) có tâm I(1;2), bán kính R = 3.

- Qua T_v^→: (C) biến thành đường tròn (C₁) tâm I₁, có tọa độ là:

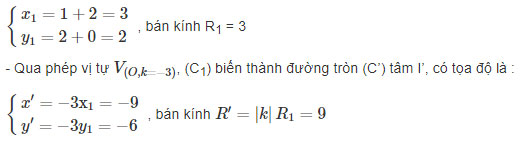
Vậy phương trình đường tròn (C’) là: (x+9)²+(x+6)²=81

Đề 2 trang 42 Sách bài tập (SBT) Hình học 11

Câu 1. (5 điểm )

Trong mặt phẳng Oxy cho đường tròn (x−1)²+(y−2)²=16. Viết phương trình đường tròn ảnh của đường tròn đã cho qua phép quay tâm O là gốc tọa độ với góc quay 90°.

Câu 2. (5 điểm )

Trong mặt phẳng Oxy cho ba đường tròn:

(C₁):(x−1)²+(y−3)²=4

(C₂):(x+3)²+(y−4)²=4

(C₃):(x+1)²+(y−5)²=5

Trong hai đường tròn (C₂) và (C₃), đường tròn nào là ảnh của (C₁) qua phép tịnh tiến. Xác định phép tịnh tiến này.

Giải:

Câu 1.

(C) có tâm I(1; 2), bán kính R = 4. Gọi I’, R’ lần lượt là tâm và bán kính của đường tròn ảnh, ta có:

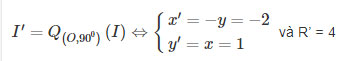
Vậy phương trình (C’) là (x+2)²+(y−1)²=16.

Câu 2.

(C₁) có tâm I₁(1;3), bán kính R₁ = 2

(C₂) có tâm I₂(−3;4), bán kính R₂ = 2

(C₃) có tâm I₃(−1;5), bán kính R₃=√5

- Vì R₃≠R₁ nên (C₃) không thể là ảnh của (C₁) qua phép tịnh tiến

- Do R₂=R₁ nên (C₂) là ảnh của (C₁) qua phép tịnh tiến T_v^→, với v^→=I₁I₂^→=(−4;1).

Đề 3 trang 42 Sách bài tập (SBT) Hình học 11

Câu 1. (5 điểm )

Cho tam giác ABC. Gọi F là phép dời hình có được bằng cách thực hiện liên tiếp các phép tịnh tiến theo thứ tự T_AB^→,T_BC^→,T_CA^→. Hỏi F là phép biến hình gì?

Câu 2. (5 điểm)

Trong mặt phẳng Oxy cho hai đường tròn:

(C₁):(x−1)²+(y+3)²=4

(C₁):(x+2)²+(y−6)²=16

Tìm phép vị tự biến (C₁) thành (C₂)

Giải:

Câu 1.

Lấy M là điểm bất kì.

Gọi M₁=T_AB^→(M),M₂=T_BC^→(M₁),M′=T_CA^→(M₂)

Ta có

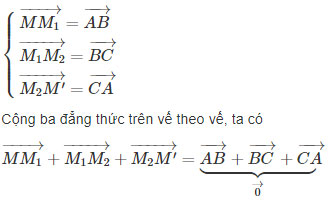
MM′^→=0^→

M′≡M

Phép biến hình F trên biến M thành M′≡M, với mọi M (F được gọi là phép đồng nhất).

Câu 2.

(C₁) có tâm I₁(1;−3), bán kính R₁ = 2

(C₂) có tâm I₂(−2;6) bán kính R₂ = 4

Gọi V_(I;k) là phép vị tự biến (C₁) thanh (C₂).

Ta có:

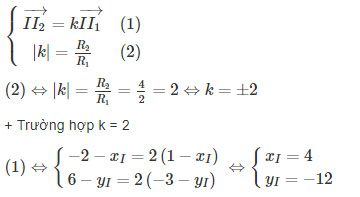
Ta được phép vị tự thứ nhất có tâm I(4; -12) tỉ số vị tự là k = 2

+ Trường hợp k = -2

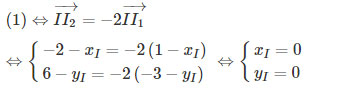
Ta được phép vị tự thứ hai có tâm I(0; 0), tỉ số vị tự là k = -2

-----------------------------------

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải SBT Toán 11 đề kiểm tra chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Sinh học lớp 11, Vật lý lớp 11, Hóa học lớp 11, Giải bài tập Toán 11 mà VnDoc tổng hợp và đăng tải.