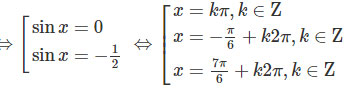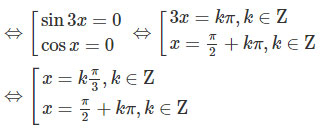Giải SBT Toán 11 bài 3: Một số phương trình lượng giác thường gặp
Toán 11 - Một số phương trình lượng giác thường gặp
VnDoc xin giới thiệu tới bạn đọc tài liệu Giải SBT Toán 11 bài 3: Một số phương trình lượng giác thường gặp, tài liệu kèm theo lời giải chi tiết sẽ là nguồn thông tin hữu ích để phục vụ công việc học tập của các bạn học sinh được tốt hơn. Mời các bạn học sinh tham khảo.
Giải SBT Toán 11 bài 3
Bài 3.1 trang 35 Sách bài tập (SBT) Đại số và giải tích 11
Giải các phương trình sau
a) cos2x−sinx−1=0
b) cosxcos2x=1+sinxsin2x
c) 4sinxcosxcos2x=−1
d) tanx=3cotx
Giải:
a)
cos2x−sinx−1=0
⇔1−2sin2x−sinx−1=0
⇔sinx(2sinx+1)=0
b)
cosxcos2x=1+sinxsin2x
⇔cosxcos2x−sinxsin2x=1
⇔cos3x=1⇔3x=k2π
⇔x=k2π/3, k∈Z
c)
4sinxcosxcos2x=−1
⇔2sin2xcos2x=−1
⇔sin4x=−1
⇔4x=−π/2+k2π, k∈Z
⇔x=−π/8+kπ/2, k∈Z
d)
tanx=3cotx. Điều kiện cosx ≠ 0 và sinx ≠ 0.
Ta có:
tanx=3/tanx
⇔tan2x=3
⇔tanx=±√3
⇔x=±π/3+kπ, k∈Z
Các phương trình này thỏa mãn điều kiện của phương trình nên là nghiệm của phương trình đã cho.
Bài 3.2 trang 35 Sách bài tập (SBT) Đại số và giải tích 11
Giải các phương trình sau
a) sinx+2sin3x=−sin5x
b) cos5xcosx=cos4x
c) sinxsin2xsin3x=1/4sin4x
d) sin4x+cos4x=−1/2cos22x
Giải:
a)
sinx+2sin3x=−sin5x
⇔sin5x+sinx+2sin3x=0
⇔2sin3xcos2x+2sin3x=0
⇔2sin3x(cos2x+1)=0
⇔4sin3xcos2x=0
b)
cos5xcosx=cos4x
⇔1/2(cos6x+cos4x)=cos4x
⇔cos6x=cos4x
⇔6x=±4x+k2π,k∈Z
⇔[2x=k2π,k∈Z;10x=k2π,k∈Z⇔[x=kπ, k∈Z;x=kπ/5, k∈Z
Tập {kπ, k ∈ Z} chứa trong tập {l.π/5, l∈Z} ứng với các giá trị l là bội số của 5, nên nghiệm của phương trình là: x=kπ5,k∈Z
c)
sinxsin2xsin3x=1/4sin4x
⇔sinxsin2xsin3x=1/2sin2xcos2x
⇔sin2x(cos2x−2sinxsin3x)=0
⇔sin2xcos4x=0

d)
sin4x+cos4x=−1/2cos22x
⇔(sin2x+cos2x)2−2sin2xcos2x=−1/2cos22x
⇔1−1/2sin22x+1/2cos22x=0
⇔1+1/cos4x=0
⇔cos4x=−2
Phương trình vô nghiệm (Vế phải không dương với mọi x trong khi vế trái dương với mọi x nên phương trình đã cho vô nghiệm).
Bài 3.3 trang 36 Sách bài tập (SBT) Đại số và giải tích 11
Giải các phương trình sau
a) 3cos2x−2sinx+2=0
b) 5sin2x+3cosx+3=0
c) sin6x+cos6x=4cos22x
d) −1/4+sin2x=cos4x
Giải:
a)
3cos2x−2sinx+2=0
⇔3(1−sin2x)−2sinx+2=0
⇔3sin2x+2sinx−5=0
⇔(sinx−1)(3sinx+5)=0
⇔sinx=1
⇔x=π/2+k2π,k∈Z
b)
5sin2x+3cosx+3=0
⇔5(1−cos2x)+3cosx+3=0
⇔5cos2x−3cosx−8=0
⇔(cosx+1)(5cosx−8)=0
⇔cosx=−1
⇔x=(2k+1)π,k∈Z
c)
sin6x+cos6x=4cos22x
⇔(sin2x+cos2x)3−3sin2xcos2x(sin2x+cos2x)=4cos22x
⇔1−3/4sin22x=4cos22x
⇔1−3/4(1−cos22x)=4cos22x
⇔13/4cos22x=1/4
⇔13(1+cos4x/2)=1
⇔1+cos4x=2/13
⇔cos4x=−11/13
⇔4x=±arccos(−11/13)+k2π, k∈Z
⇔x=±14arccos(−11/13)+kπ/2, k∈Z
d)
−1/4+sin2x=cos4x
⇔−1/4+1−cos2x/2=1+cos2x/2)2⇔−1+2−2cos2x=1+2cos2x+cos22x
⇔cos22x+4cos2x=0
⇔[cos2x=0;cos2x=−4 (Vônghiệm)
⇔2x=π/2+kπ, k∈Z
⇔x=π/4+k.π/2, k∈Z
Bài 3.4 trang 36 Sách bài tập (SBT) Đại số và giải tích 11
Giải các phương trình sau
a) 2tanx−3cotx−2=0
b) cos2x=3sin2x+3
c) cotx−cot2x=tanx+1
Giải
a) 2tanx−3cotx−2=0 Điều kiện cosx ≠ 0 và sinx ≠ 0
Ta có
2tanx−3/tanx−2=0
⇔2tan2x−2tanx−3=0
⇔tanx=1±√7/2
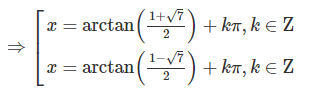
Các giá trị này thỏa mãn điều kiện nên là nghiệm của phương trình
b) cos2x=3sin2x+3
Ta thấy cosx = 0 không thỏa mãn phương trình. Với cosx ≠ 0, chia hai vế của phương trình cho cos2x ta được:
1=6tanx+3(1+tan2x)
⇔3tan2x+6tanx+2=0
⇔tanx=−3±√3/3
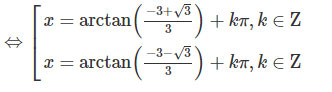
c) cotx−cot2x=tanx+1 (1)
Điều kiện: sinx ≠ 0 và cosx ≠ 0. Khi đó:
(1)⇔cosx/sinx−cos2x/sin2x=sinx/cosx+1
⇔2cos2x−cos2x=2sin2x+sin2x
⇔2(cos2x−sin2x)−cos2x=sin2x
⇔cos2x=sin2x
⇔tan2x=1
⇒2x=π/4+kπ, k∈Z
⇒x=π/8+k.π/2, k∈Z(1)
Các giá trị này thỏa mãn điều kiện nên là nghiệm của phương trình
Bài 3.5 trang 36 Sách bài tập (SBT) Đại số và giải tích 11
Giải các phương trình sau
a) cos2x+2sinxcosx+5sin2x=2
b) 3cos2x−2sin2x+sin2x=1
c) 4cos2x−3sinxcosx+3sin2x=1
Giải
a) cos2x+2sinxcosx+5sin2x=2
Rõ ràng cosx = 0 không thỏa mãn phương trình. Với cosx ≠ 0, chia hai vế cho cos2x ta được:
1+2tanx+5tan2x=2(1+tan2x)
⇔3tan2x+2tanx−1=0
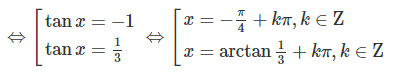
b) 3cos2x−2sin2x+sin2x=1
Với cosx = 0 ta thấy hai vế đều bằng 1. Vậy phương trình có nghiệm x=π/2+kπ, k∈Z
Trường hợp cosx ≠ 0, chia hai vế cho cos2x ta được:
3−4tanx+tan2x=1+tan2x
⇔4tanx=2
⇔tanx=1/2
⇔x=arctan1/2+kπ, k∈Z
Vậy nghiệm của phương trình là x=π/2+kπ, k∈Z và x=arctan1/2+kπ, k∈Z
c) 4cos2x−3sinxcosx+3sin2x=1
Rõ ràng cosx ≠ 0, chia hai vế của phương trình cho cos2x ta được:
4−3tanx+3tan2x=1+tan2x
⇔2tan2x−3tanx+3=0
Phương trình cuối vô nghiệm đối với tanx, do đó phương trình đã cho vô nghiệm
Bài 3.6 trang 36 Sách bài tập (SBT) Đại số và giải tích 11
Giải các phương trình sau
a) 2cosx−sinx=2
b) sin5x+cos5x=−1
c) 8cos4x−4cos2x+sin4x−4=0
d) sin6x+cos6x+1/2sin4x=0
Giải
a)
2cosx−sinx=2
⇔√5(2/√5cosx−1/√5.sinx)=2
Kí hiệu α là góc mà cosα=2/√5 và sinα=−1/√5, ta được phương trình
cosαcosx+sinαsinx=2/√5
⇔cos(x−α)=cosα
⇔x−α=±α+k2π,k∈Z
⇔[x=2α+k2π,k∈Z;x=k2π,k∈Z
b)
sin5x+cos5x=−1
⇔√2(√2/2sin5x+√2/2cos5x)=−1
⇔cosπ/4sin5x+sinπ/4cos5x=−√2/2
⇔sin(5x+π/4)=sin(−π/4)
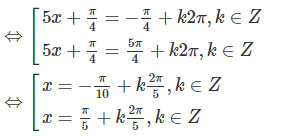
c)
8cos4x−4cos2x+sin4x−4=0
⇔8(1+cos2x/2)2−4cos2x+sin4x−4=0
⇔2(1+2cos2x+cos22x)−4cos2x+sin4x−4=0
⇔2cos22x+sin4x−2=0
⇔1+cos4x+sin4x−2=0
⇔cos4x+sin4x=1
⇔sin(4x+π/4)=sin.π/4
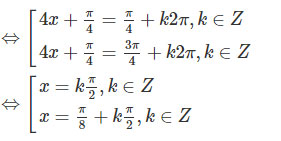
d)
sin6x+cos6x+1/2sin4x=0
⇔(sin2x+cos2x)3−3sin2xcos2x(sin2x+cos2x)+1/2sin4x=0
⇔1−3sin2xcos2x+1/2sin4x=0
⇔1−3(sin2x/2)2+1/2sin4x=0
⇔1−3/4.sin22x+1/2sin4x=0
⇔1−3/4.1−cos4x/2+1/2sin4x=0
⇔8−3+3cos4x+4sin4x=0
⇔3cos4x+4sin4x=−5
⇔3/5cos4x+4/5sin4x=−1
Kí hiệu α là cung mà sinα=3/5,cosα=4/5 ta được:
⇔sin(4x+α)=−1
⇔4x+α=3π/2, k∈Z
⇔x=3π/8−α/4+k.π/2, k∈Z
Bài 3.7 trang 36 Sách bài tập (SBT) Đại số và giải tích 11
Giải các phương trình sau:
a) 1+sinx−cosx−sin2x+2cos2x=0
b) sinx−1/sinx=sin2x−1/sin2x
c) cosxtan3x=sin5x
d) 2tan2x+3tanx+2cot2x+3cotx+2=0
Giải:
a) 1+sinx−cosx−sin2x+2cos2x=0 (1)
Ta có:
1−sin2x=(sinx−cosx)2;
2cos2x=2(cos2x−sin2x)
=−2(sinx−cosx)(sinx+cosx)
Vậy
(1)⇔(sinx−cosx)(1+sinx−cosx−2sinx−2cosx)=0
⇔(sinx−cosx)(1−sinx−3cosx)=0
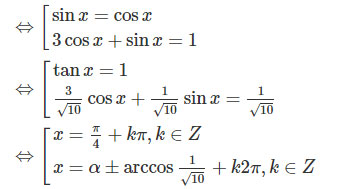
trong đó, cosα=3/√10, sinα=1/√10
b) sinx−1/sinx=sin2x−1/sin2x (2)
Điều kiện sinx ≠ 0
(2)⇔(sinx−sin2x)+(1/sin2x−1/sinx)=0
⇔sinx(1−sinx)+1−sinx/sin2x=0
⇔(1−sinx)(sin3x+1)=0
⇔[sinx=1;sinx=−1⇒x=π/2+kπ, k∈Z
(thỏa mãn điều kiện)
c) cosxtan3x=sin5x(3)
Điều kiện: cos3x ≠ 0. Khi đó,
(3)⇔cosxsin3x=cos3xsin5x
⇔1/2(sin4x+sin2x)=1/2(sin8x+sin2x)
⇔sin8x=sin4x
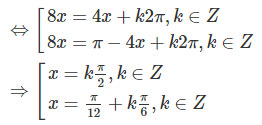
Kết hợp với điều kiện ta được nghiệm của phương trình là:
x=kπ,k∈Z và x=π/12+k.π/6, k∈Z
d) 2tan2x+3tanx+2cot2x+3cotx+2=0 (4)
Điều kiện: cosx ≠ 0 và sinx ≠ 0. Khi đó,
(4)⇔2(tan2x+cot2x)+3(tanx+cotx)+2=0
⇔2[(tanx+cotx)2−2]+3(tanx+cotx)+2=0
Đặt t = tanx + cotx ta được phương trình
2t2+3t−2=0⇒t=−2,t=1/2
Với t = -2 ta có tanx + cotx = -2
⇔tan2x+2tanx+1=0⇒tanx=−1
⇒x=−π/4+kπ, k∈Z
(thỏa mãn điều kiện)
Với t=1/2 ta có tanx+cotx=1/2⇔2tan2x−tanx+2=0
Phương trình này vô nghiệm.
Vậy nghiệm của phương trình (4) là x=−π/4+kπ, k∈Z
Bài 3.8 trang 36 Sách bài tập (SBT) Đại số và giải tích 11
Giải phương trình
cotx−tanx+4sin2x=2/sin2x
Giải
Hướng dẫn: Đối với những phương trình lượng giác chứa tanx, cotx, sin2x hoặc cos2x, ta có thể đưa về phương trình chứa cosx, sinx, sin2x, hoặc cos2x ngoài ra cũng có thể đặt ẩn phụ t = tanx để đưa về một phương trình theo t.
Cách 1: Điều kiện của phương trình:
sin2x≠0⇔cos2x≠±1 (1)
Ta có:
cotx−tanx+4sin2x=2/sin2x
⇔cosx/sinx−sinx/cosx+4sin2x−2/sin2x=0
⇔cos2x−sin2x/sinx.cosx+4sin2x−2/sin2x=0
⇔2cos2x/sin2x+4sin2x−2/sin2x=0
⇔2cos2x+4sin22x−2=0
⇔cos2x+2(1−cos22x)−1=0
⇔2cos22x−cos2x−1=0
⇔[cos2x=1(loại);cos2x=−1;2
⇔2x=±2π/3+k2π, k∈Z
⇔x=±π/3+kπ, k∈Z
Cách 2. Đặt t = tanx
Điều kiện t ≠ 0
Phương trình đã cho có dạng
1/t−t+4.2t/1+t2=1+t2/t
⇔1−t2/t+8t/1+t2−1+t2/t=0
⇔1−t4+8t2−(1+t2)2=0
⇔−2t4+8t2−2t2=0
⇔t4−3t2=0
⇒t2(t3−3)=0
⇔[t=0(loại do(2));t=±√3
tanx=±√3⇔x=±π/3+kπ, k∈Z
-----------------------------------
Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải SBT Toán 11 bài 3: Một số phương trình lượng giác thường gặp. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Sinh học lớp 11, Vật lý lớp 11, Hóa học lớp 11, Giải bài tập Toán 11 mà VnDoc tổng hợp và đăng tải.