Giải SBT Toán 11 ôn tập chương 5: Đạo hàm

Toán 11 - Đạo hàm

VnDoc xin giới thiệu tới thầy cô và các bạn học sinh tài liệu Giải SBT Toán 11 ôn tập chương 5: Đạo hàm, chắc chắn tài liệu sẽ giúp các bạn học sinh học tập môn Toán được tốt hơn. Mời thầy cô và các bạn học sinh cùng tham khảo.

Giải SBT Toán 11 ôn tập chương 5

Bài 1 trang 214 Sách bài tập (SBT) Đại số và giải tích 11

Tìm đạo hàm của các hàm số sau:

a) y=xcot²x

b) y=sin√x/cos3x

c) y=(sin2x+8)³

d) y=(2x³−5)tanx

Giải:

\(a)\cot2x-\frac{2x\cos}{x\sin^3x}\)

\(b)\frac{\cos\sqrt{x}\cos3x+6\sqrt{x}\sin\sqrt{x}\sin3x}{2\sqrt{x}\cos^23x}\)

c) 6cos2x(sin2x+8)²

\(d)6x2\tan x+\frac{2x^3-5.}{\cos^2x}\)

Bài 2 trang 214 Sách bài tập (SBT) Đại số và giải tích 11

Giải phương trình f′(x)=g(x), biết rằng

a) f(x)=1−cos3x/3;g(x)=(cos6x−1)cot3x

b) f(x)=1/2cos2x;g(x)=1−(cos3x+sin3x)²

c) f(x)=1/2sin2x+5cosx;g(x)=3sin²x+3/1+tan²x.

Giải:

a) f(x)=1−cos3x/3⇒f′(x)=sin3x. Ta có

f′(x)=g(x)⇔(cos6x−1).cot3x=sin3x (điều kiện: sin3x≠0⇔cos3x≠±1)

⇔(cos6x−1).cos3x=sin²3x

⇔(1−2sin²3x−1).cos3x=sin²3x

⇔sin²3x.(2cos3x+1)=0

⇔cos3x=−1/2(vìsin3x≠0)

⇔cos3x=cos2π/3

⇔3x=±2π/3+k2π

⇔x=±2π/9+k.2π/3(k∈Z).

b) f(x)=1/2cos2x⇒f′(x)=−sin2x. Ta có

f′(x)=g(x)

⇔−sin2x=1−(cos3x+sin3x)²

⇔1+sin2x=(cos3x+sin3x)²

⇔1+sin2x=1+2sin3xcos3x

⇔sin6x−sin2x=0

⇔2cos4xsin2x=0

⇔cos4x=0;sin2x=0

⇔4x=π/2+kπ;2x=nπ

⇔x=π/8+k.π/4;x=n.π/2(k,n∈Z).

c) f(x)=1/2sin2x+5cosx⇒f′(x)=cos2x−5sinx. Ta có

f′x)=g(x)

⇔cos2x−5sinx=3sin²x+3/1+tan2x

⇔5sinx+3/1+tan²x=cos2x−3sin²x

⇔5sinx+3cos²x=cos²x−4sin²x

⇔5sinx=−2cos²x−4sin²x

⇔5sinx=−2−2sin²x

⇔2sin²x+5sinx+2=0

Đặt t=sinx,t∈[−1;1], ta có phương trình 2t²+5t+2=0

Giải phương trình t=−1/2 ta được (loại t = -2 ).

sinx=−1/2

⇔sinx=sin(−π/6)

⇔x=−π/6+k2π;x=7π/6+k2π(k∈Z).

Bài 3 trang 214 Sách bài tập (SBT) Đại số và giải tích 11

Tìm đạo hàm của hàm số tại điểm đã chỉ ra :

a) f(x)=\(\frac{\sqrt{x+1}}{\sqrt{x+1}+1}\), f′(0)=?

b) y=(4x+5)², y′(0)=?

c) g(x)=sin4xcos4x, g′(π/3)=?

Giải:

a) 1818

b) 40

c) -2

Bài 4 trang 214 Sách bài tập (SBT) Đại số và giải tích 11

Chứng minh rằng f′(x)>0∀x∈R, nếu

a) f(x)=2/3x⁹−x⁶+2x³−3x²+6x−1

b) f(x)=2x+sinx

Giải:

a)

f′(x)=6(x⁸−x⁵+x²−x+1)

=6x²(x⁶−x³+1/4)+3x²+6(x²/4−x+1)

=6x²(x³−1/2)²+3x²+6(x/2−1)²>0,∀x∈R.

b) f′(x)=2+cosx>0,∀x∈R.

Bài 5 trang 214 Sách bài tập (SBT) Đại số và giải tích 11

Xác định a để f′(x)>0∀x∈R, biết rằng

f(x)=x³+(a−1)x²+2x+1

Giải:

f′(x)=3x²+2(a−1)x+2

Δ′=(a−1)²−6=a²−2a−5. Ta phải có

Δ′<0⇔a²−2a−5<0⇔1−√6<a<1+√6

Vậy f′(x)>0 với mọi x∈R nếu 1−√6<a<1+√6.

Bài 6 trang 214 Sách bài tập (SBT) Đại số và giải tích 11

Xác định a để g′(x)≥0∀x∈R biết rằng

g(x)=sinx−asin2x−1/3sin3x+2ax

Giải:

g′(x)=cosx−2acos2x−cos3x+2a

=4asin²x+2sinxsin²x

=4asin²x+4sin²xcosx

=4sin²x(a+cosx)

Rõ ràng với a > 1 thì a+cosx>0 và sin²x≥0 với mọi x∈R nên với a > 1 thì g′(x)≥0,∀x∈R.

Bài 7 trang 215 Sách bài tập (SBT) Đại số và giải tích 11

Tìm hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm y=tanx có hoành độ x₀=π/4

Giải:

Đáp số: 2

Bài 8 trang 215 Sách bài tập (SBT) Đại số và giải tích 11

Trên đường cong y=4x²−6x+3, hãy tìm điểm tại đó tiếp tuyến song song với đường thẳng y=2x

Giải:

Đáp số: (1; 1)

Bài 9 trang 215 Sách bài tập (SBT) Đại số và giải tích 11

Đồ thị hàm số y=1/√3.sin3x cắt trục hoành tại gốc toạ độ dưới một góc bao nhiêu độ (góc giữa trục hoành và tiếp tuyến của đồ thị tại giao điểm)?

Giải:

Đáp số: 60^o.

Bài 10 trang 215 Sách bài tập (SBT) Đại số 11 và giải tích 11

Cho hàm số

f(x)=x³+bx²+cx+d; (C)

g(x)=x²−3x−1.

a) Xác định b, c, d sao cho đồ thị (C) đi qua các điểm (1;3),(−1;−3) và f′(1/3)=5/3

b) Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ x₀=1

c) Giải phương trình f′(sint)=3

d) Giải phương trình f′′(cost)=g′(sint)

e) Tìm giới hạn lim_z→0f′′(sin5z)+2/g′(sin3z)+3

Giải:

a)

c=2,b=−1,d=1

⇒f(x)=x³−x²+2x+1

b) f′(x)=3x²−2x+2⇒f′(1)=3

Phương trình tiếp tuyến tại M(1;3) là

y−3=3(x−1) hay y=3x

c)

f′(sint)=3sin²t−2sint+2

f′(sint)=3

⇔3sin²t−2sint−1=0

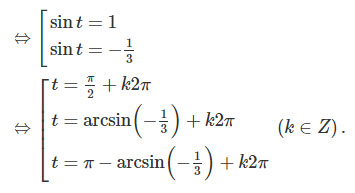
d)

f′′(x)=6x−2

⇒f′′(cost)=6cost−2

g′(x)=2x−3

⇒g′(sint)=2sint−3

Vậy

6cost−2=2sint−3

⇔2sint−6cost=1

⇔sint−3cost=1/2

Đặt tanφ=3, ta được

sin(t−φ)=1/2cosφ=α. Suy ra

t=φ+arcsinα+k2π

t=π+φ−arcsinα+k2π(k∈Z).

e)

lim_z→0f′′(sin5z)+2/g′(sin3z)+3=lim_z→06sin5z/2sin3z=5lim_z→0\(\frac{\frac{\sin5z}{5z}}{\frac{\sin3z}{3z}}=5\)

-----------------------------------

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải SBT Toán 11 ôn tập chương 5: Đạo hàm. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Sinh học lớp 11, Vật lý lớp 11, Hóa học lớp 11, Giải bài tập Toán 11 mà VnDoc tổng hợp và đăng tải.