Giải SBT Toán 11 bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song

Toán 11 - Hai đường thẳng chéo nhau và hai đường thẳng song song

Để giúp các bạn học sinh có kết quả cao hơn trong học tập, VnDoc mời các bạn tham khảo Giải SBT Toán 11 bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song, tài liệu kèm theo lời giải chi tiết sẽ giúp các bạn học sinh học tập tốt môn Toán đơn giản hơn.

Giải SBT Toán 11 bài 2

Bài 2.10 trang 70 Sách bài tập (SBT) Hình học 11

Cho hình chóp S.ABCD có đáy là hình hình hành ABCD. Tìm giao tuyến của các cặp mặt phẳng sau đây:

a) (SAC) và (SBD);

b) (SAB) và (SCD);

c) (SAD) và (SBC)

Giải:

(h.2.28)

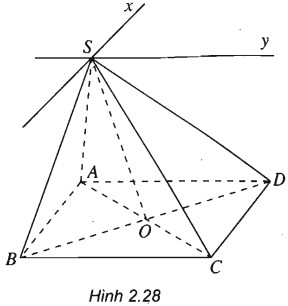
a)

Ta có

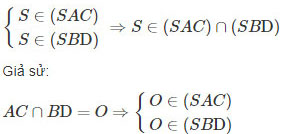
⇒O∈(SAC)∩(SBD)

⇒(SAC)∩(SBD)=SO

b) Ta có:

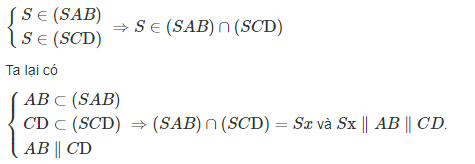
c) Lập luận tương tự câu b) ta có ⇒(SAD)∩(SBC)=Sy và Sy∥AD∥BC

Bài 2.11 trang 70 Sách bài tập (SBT) Hình học 11

Cho tứ diện ABCD. Trên các cạnh AB và AC lần lượt lấy các điểm M và N sao cho. Tìm giao tuyến của hai mặt phẳng (DBC) và (DMN).

Giải:

(h.2.29)

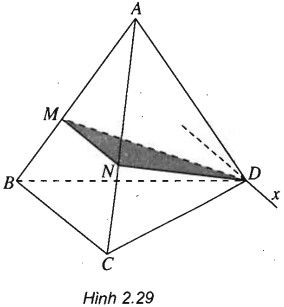
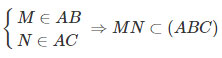
Trong tam giác ABC ta có:

AM/AB=AN/AC⇒MN∥BC

Hiển nhiên D∈(DBC)∩(DMN)

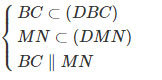
⇒(DBC)∩(DMN)=Dx và Dx∥BC∥MN

Bài 2.12 trang 70 Sách bài tập (SBT) Hình học 11

Cho tứ diện ABCD. Cho I và J tương ứng là trung điểm của BC và AC, M là một điểm tùy ý trên cạnh AD.

a) Tìm giao tuyến d của hai mặt phẳng (MIJ) và (ABD)

b) Gọi N là giao điểm của BD với giao tuyến d, K là giao điểm của IN và IM. Tìm tập hợp điểm K khi M di động trên đoạn AD (M không là trung điểm của AD).

c) Tìm giao tuyến của hai mặt phẳng (ABK) và (MIJ).

Giải:

(h.2.30)

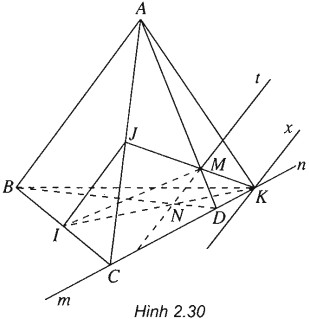
a)

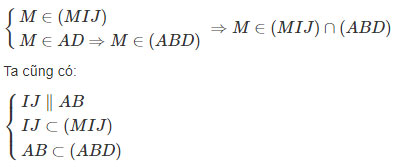
⇒(MIJ)∩(ABD)=d=Mt và Mt∥AB∥IJ

b) Ta có: Mt∥AB⇒Mt∩BD=N

IN∩JM=K

⇒K∈IN;K∈JM

Vì K∈IN⇒K∈(BCD)

Và K∈JM⇒K∈(ACD)

Mặt khác (BCD)∩(ACD)=CD do đó K∈CD. Do vậy K nằm trên hai nửa đường thẳng Cm và Dn thuộc đường thẳng CD. (Để ý rằng nếu M là trung điểm của AD thì sẽ không có điểm K.)

c) Ta có:

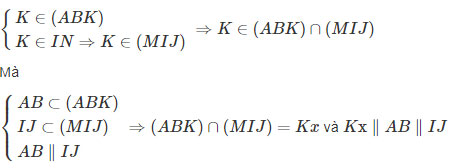
Bài 2.13 trang 71 Sách bài tập (SBT) Hình học 11

Cho tứ diện ABCD. Gọi M, N, P, Q, R và S lần lượt trung điểm của AB, CD, BC, AD, AC và BD. Chứng minh rằng tứ giác MNPQ là hình bình hành. Từ đó suy ra ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.

Giải:

(h.2.31)

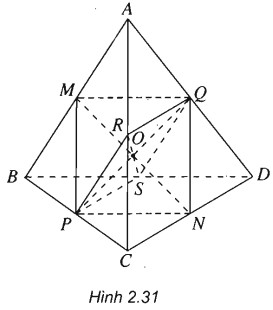
Trong tam giác ABC ta có:

MP∥AC và MP=AC/2

Trong tam giác ACD ta có:

QN∥AC và QN=AC/2.

Từ đó suy ra MP∥QN\MP=QN

⟹ Tứ giác MNPQ là hình bình hành.

Do vậy hai đường chéo MN và PQ cắt nhau tại trung điểm O của mỗi đường.

Tương tự: PR∥QS và PR=QS=AB/2. Do đó tứ giác PQRS là hình bình hành.

Suy ra hai đường chéo RS và PQ cắt nhau tại trung điểm O của PQ và OR = OS

Vậy ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.

Bài 2.14 trang 71 Sách bài tập (SBT) Hình học 11

Cho tứ diện ABCD có I và J lần lượt là trọng tâm các tam giác ABC và ABD. Chứng minh rằng.

Giải:

(h.2.32)

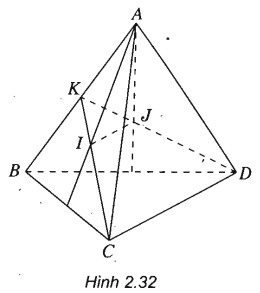
Gọi K là trung điểm của AB.

Vì I là trọng tâm của tam giác ABC nên I∈KC và vì J là trọng tâm của tam giác ABD nên J∈KD.

Từ đó suy ra KI/KC=KJ/KD=1/3⇒IJ∥CD.

Bài 2.15 trang 71 Sách bài tập (SBT) Hình học 11

Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy là AD và BC. Biết AD = a, BC = b. Gọi I và J lần lượt là trọng tâm của các tam giác SAD và SBC. Mặt phẳng (ADJ) cắt SB, SC lần lượt tại M, N. Mặt phẳng (BCI) cắt SA, SD lần lượt tại P, Q.

a) Chứng minh MN song song với PQ.

b) Giả sử AM cắt BP tại E; CQ cắt DN tại F. Chứng minh rằng EF song song với MN và PQ. Tính EF theo a và b.

Giải:

(h.2.33)

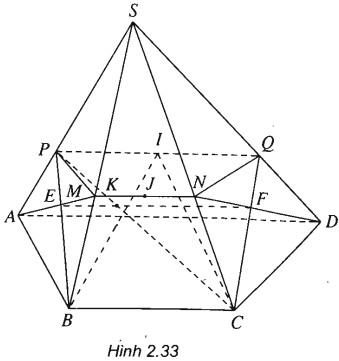
a)

Ta có: I∈(SAD)⇒I∈(SAD)∩(IBC)

Vậy

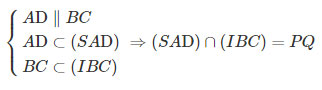
và PQ∥AD∥BC(1)

Tương tự: J∈(SBC)⇒J∈(SBC)∩(JAD)

Vậy

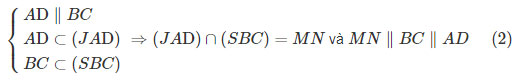
Từ (1) và (2) suy ra PQ∥MN

b) Ta có:

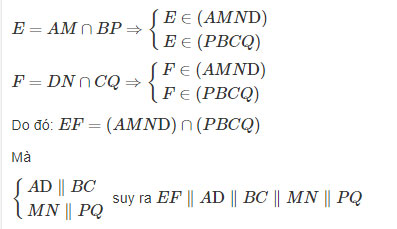
Tính

EF:CP∩EF=K⇒EF=EK+KF

EK∥BC⇒EK/BC=PE/PB(∗)

PM∥AB⇒PE/EB=PM/AB

Mà PM/AB=SP/SA=2/3 suy ra PE/EB=2/3

Từ (*) suy ra

EK/BC=PE/PB=PE/PE+EB

=1/1+EB/PE=1/1+3/2=2/5

⇒EK=2/5.BC=2/5.b

Tương tự ta tính được KF=2/5.a

Vậy: EF=2/5.a+2/5.b=2/5(a+b)

-----------------------------------

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải SBT Toán 11 bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Sinh học lớp 11, Vật lý lớp 11, Hóa học lớp 11, Giải bài tập Toán 11 mà VnDoc tổng hợp và đăng tải.