Giải SBT Toán 11 bài 2: Dãy số
Toán 11 - Dãy số
Mời quý thầy cô và các bạn học sinh tham khảo tài liệu Giải SBT Toán 11 bài 2: Dãy số, với nội dung tài liệu sẽ giúp các bạn học sinh rèn luyện giải bài tập Toán được nhanh hơn, quý thầy cô phục vụ trong công việc giảng dạy được tốt hơn.
Giải SBT Toán 11 bài 4: Phép thử và biến cố
Giải SBT Toán 11 bài 5: Xác suất của biến cố
Giải SBT Toán 11 bài 2
Bài 2.1 trang 111 Sách bài tập (SBT) Đại số và giải tích 11
Viết 5 số hạng đầu và khảo sát tính tăng, giảm của các dãy số (un) biết
a) un=101−2n
b) un=3n−7
c) un=2n+1/n2
d) un=3n√n/2n
Giải:
a) 1/10,1/103,1/105,1/107,1/109 Dự đoán dãy (un) giảm.
Để chứng minh, ta xét tỉ số un+1/un=101−2(n+1)/101−2n=1/102<1. Vậy dãy số giảm
b) - 4, 2, 20, 74, 236. Xét dấu của hiệu un+1−un
c) 3,3/4,3/9,3/16,3/25. Làm tương tự câu b).
d) 3/2,9√2/4,27√3/8,81√4/16,243√5/32 Phần tiếp theo có thể làm tương tự câu a).
Chú ý. Qua bốn bài tập trên, học sinh có thể rút ra nhận xét về tính hợp lí của việc xét hiệu un+1−un hay tỉ số un+1/un khi khảo sát tính đơn điệu của dãy số.
Bài 2.2 trang 111 Sách bài tập (SBT) Đại số và giải tích 11
Trong các dãy số (un) cho dưới đây, dãy số nào bị chặn dưới, bị chặn trên và bị chặn?
a) un=2n−n2
b) un=n+1/n
c) un=![]() \(\sqrt{n^2-4n+7}\)
\(\sqrt{n^2-4n+7}\)
d) un=1/n2−6n+11
Giải:
a) Bị chặn trên vì un≤1,∀n∈N∗
b) Bị chặn dưới vì un≥2,∀n∈N∗
c) Bị chặn dưới vì un≥√3,∀n∈N∗u
d) Bị chặn vì 0<un≤12,∀n∈N∗
Bài 2.3 trang 111 Sách bài tập (SBT) Đại số và giải tích 11
Cho dãy số (un) xác định bởi
{u1=5;un+1=un+3n−2 với n≥1
a) Tìm công thức tính (un) theo n;
b) Chứng minh (un) là dãy số tăng.
Giải:
a) ĐS: un=5+(n−1)(3n−4)/2
b) Tương tự bài Bài 2.1
Bài 2.4 trang 112 Sách bài tập (SBT) Đại số và giải tích 11
Cho dãy số (un) với
a) Viết công thức truy hồi của dãy số;
b) Chứng minh dãy số bị chặn dưới;
c) Tính tổng n số hạng đầu của dãy đã cho.
Giải:
a) Ta có u1=0
Xét hiệu un+1−un=(n+1)2−4(n+1)+3−n2+4n−3=2n−3
Vậy công thức truy hồi là
{u1=0;un+1=un+2n−3 với n≥1
b) un=n2−4n+3=(n−2)2−1≥−1. Vậy dãy số bị chặn dưới nhưng không bị chặn trên.
c)
Sn=1+22+32+...+n2−4(1+2+...+n)+3n
=n(n+1)(2n+1)/6−4.n(n+1)/2+3n
=n(n+1)(2n+1)−12n(n+1)+18n/6
=n(n+1)(2n−11)+18n/6
Bài 2.5 trang 112 Sách bài tập (SBT) Đại số và giải tích 11
Cho dãy số (un) với (un)=1+(n−1).2n
a) Viết năm số hạng đầu của dãy số;
b) Tìm công thức truy hồi;
c) Chứng minh (un) là dãy số tăng và bị chặn dưới.
Giải:
a) Học sinh tự giải.
b) HD: Tìm hiệu un+1−un
ĐS:
{u1=1;un+1=un+(n+1)2n với n≥1
c) HD: Xét dấu un+1−un
Bài 2.6 trang 112 Sách bài tập (SBT) Đại số và giải tích 11
Các dãy số (un), (vn)được xác định bằng công thức
a) {u1=1;un+1=un+n3 với n≥1;
b) {v1=2;vn+1=v2n với n≥1
Tìm công thức tính (un), (vn) theo n. Tính số hạng thứ 100 của dãy số (un). Hỏi số 4294967296 là số hạng thứ mấy của dãy số (vn)
Giải:
a) Từ un+1−un=n3 ta có
u1=1;
u2−u1=13;
u3−u2=23;...un−1−un−2=(n−2)3;
un−un−1=(n−1)3
Cộng từng vế n đẳng thức trên và rút gọn, ta được
un=1+13+23+...+(n−1)3
Sử dụng kết quả bài tập 12 b) - ta có
13+23+...+(n−1)3=(n−1)2n2/4
Vậy
un=1+n2(n−1)2/4
u100=24502501
b) Hãy viết một vài số hạng đầu của dãy và quan sát
v1=2;
v2=v21=22;
v3=v22=24=![]() \(2^{2^2}\);
\(2^{2^2}\);
v4=v23=28=![]() \(2^{2^3}\)
\(2^{2^3}\)
Từ đây dự đoán vn=![]() \(2^{2^{n-1}}\)
\(2^{2^{n-1}}\)
Công thức trên dễ dàng chứng minh bằng phương pháp quy nạp. Số 4294967296 là số hạng thứ sáu của dãy số (vn)
Bài 2.7 trang 112 Sách bài tập (SBT) Đại số và giải tích 11
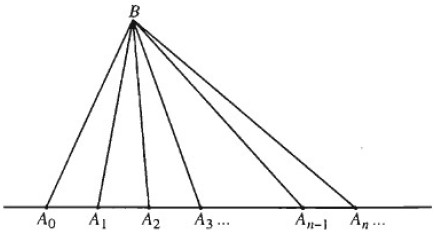
Dãy số (xn) được biểu diễn trên trục số bởi tập hợp các điểm, kí hiệu là A:
A={A0,A1,A2,...,An}
Gọi B là điểm nằm ngoài trục số. Người ta dựng các tam giác đỉnh B và hai đỉnh còn lại thuộc tập hợp A.
Đặt un là số các tam giác được tạo thành từ B và hai trong số n + 1 điểm A0,A1,A2,...,An rồi lập dãy số un
a) Tính u1,u2,u3,u4
b) Chứng minh rằng un=C2n+1 và ![]() \({u_{n + 1}} = {u_n} + n + 1\)\)
\({u_{n + 1}} = {u_n} + n + 1\)\)
Giải:
a)
u1=1
u2=3
u3=6
u4=10
b) Số các tam giác un tạo thành từ B và n + 1 điểm chính là số tổ hợp chập 2 của n + 1 phần tử:
Áp dụng công thức Ckn=Ckn−1+Ck−1n−1
Ta có C2n+2=C2n+1+C1n+1
Hay un+1=un+n+1
Bài 2.8 trang 112 Sách bài tập (SBT) Đại số và giải tích 11
Cho dãy số (un) thoả mãn điều kiện: Với mọi n ∈ N* thì 0<un<1 và un+1<1−1/4un
Chứng minh dãy số đã cho là dãy giảm.
Giải:
Vì 0<un<1 với mọi n nên 1−un+1>0
Áp dụng bất đẳng thức Cô – si ta có un+1(1−un+1)≤1/4
Mặt khác, từ giả thiết un+1<1−1/4un
suy ra un+1.un<un−1/4 hay 1/4<un(1−un+1)
So sánh (1) và (2) ta có:
un+1(1−un+1)<un(1−un+1) hay un+1<un
-----------------------------------
Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải SBT Toán 11 bài 2: Dãy số. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Sinh học lớp 11, Vật lý lớp 11, Hóa học lớp 11, Giải bài tập Toán 11 mà VnDoc tổng hợp và đăng tải.








