Giải SBT Toán 11 bài 4: Hai mặt phẳng song song
Toán 11 - Hai mặt phẳng song song
VnDoc xin giới thiệu tới thầy cô và các bạn học sinh tài liệu Giải SBT Toán 11 bài 4: Hai mặt phẳng song song, với bộ câu hỏi bài tập kèm theo lời giải chi tiết sẽ giúp các bạn học sinh có kết quả cao hơn trong học tập.
Giải SBT Toán 11 đề kiểm tra chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng
Giải SBT Toán 11 bài 1: Đại cương về đường thẳng và mặt phẳng
Giải SBT Toán 11 bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song
Giải SBT Toán 11 bài 4
Bài 2.22 trang 79 Sách bài tập (SBT) Hình học 11
Cho tứ diện ABCD. Gọi lần lượt là trọng tâm các tam giác. Chứng minh rằng.
Giải:
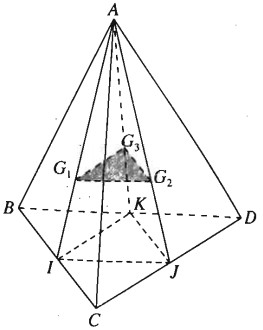
Gọi I, J và K lần lượt là trung điểm của các cạnh BC, CD và BD. Theo tính chất trọng tâm của tam giác ta có:
AG1/AI=AG2/AJ=AG3/AK=2/3
⇒G1G2∥IJ
IJ⊂(BCD)⇒G1G2∥(BCD)
Tương tự ta có G2G3∥(BCD)
G1G2,G2G3⊂(G1G2G3)
(G1G2G3)∥(BCD)
Bài 2.23 trang 79 Sách bài tập (SBT) Hình học 11
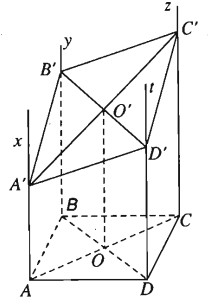
Từ bốn đỉnh của hình bình hành ABCD vẽ bốn nửa đường thẳng song song cùng chiều Ax, By, Cz và Dt sao cho chúng cắt mặt phẳng (ABCD). Một mặt phẳng (α) cắt bốn nửa đường thẳng theo thứ tự nói trên tại A’, B’, C’ và D’.
a) Chứng minh rằng (Ax,By)∥(Cz,Dt) và (Ax,Dt)∥(By,Cz)
b) Tứ giác A’B’C’D’ là hình gì?
c) Chứng minh AA′+CC′=BB′+DD′.
Giải:
a) Ta có:
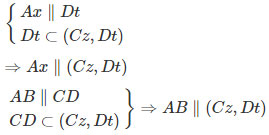
Từ Ax,AB⊂(Ax,By) suy ra (Ax,By)∥(Cz,Dt)
Tương tự ta có (Ax,Dt)∥(By,Cz)
b)
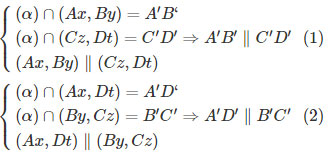
Từ (1) và (2) suy ra tứ giác A’B’C’D’ là hình bình hành.
c) Gọi O, O’ lần lượt là tâm các hình bình hành ABCD, A’B’C’D’. Dễ thấy OO’ là đường trung bình của hình thang AA’, suy ra OO′=AA′+CC′/2
Tương tự ta có:
OO′=BB′+DD′/2⇒AA′+CC′=BB′+DD′
Bài 2.24 trang 80 Sách bài tập (SBT) Hình học 11
Cho hai hình vuông ABCD và ABEF ở trong hai mặt phẳng phân biệt. Trên các đường chéo AC và BF lần lượt lấy các điểm M và N sao cho AM = BN. Các đường thẳng song song với AB vẽ từ M và N lần lượt cắt AD và AF tại M’ và N’. Chứng minh
a) (ADF)∥(BCE).
b) M′N′∥DF.
c) (DEF)∥(MM′N′N) và MN∥(DEF).
Giải:
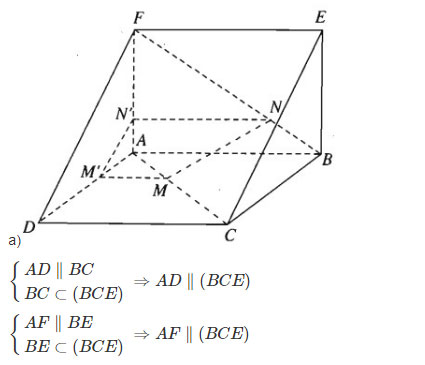
Mà AD,AF⊂(ADF)
Nên (ADF)∥(BCE)
b) Vì ABCD và ABEF là các hình vuông nên AC = BF. Ta có:
MM′∥CD⇒AM′/AD=AM/AC(1)
NN′∥AB⇒AN′/AF=BN/BF(2)
So sánh (1) và (2) ta được AM′/AD=AN′/AF⇒M′N′∥DF
c) Từ chứng minh trên suy ra DF∥(MM′N′N)
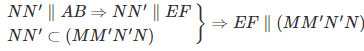
Mà DF,EF⊂(DEF) nên (DEF)∥(MM′N′N)
Vì MN⊂(MM′N′N) và (MM′N′N)∥(DEF) nên MN∥(DEF).
Bài 2.25 trang 80 Sách bài tập (SBT) Hình học 11
Cho hình lăng trụ tam giác ABCA’B’C’ có các cạnh bên là AA’, BB’, CC’. Gọi I và I’tương ứng là trung điểm của hai cạnh BC và B’C’.
a) Chứng minh rằng AI∥A′I′
b) Tìm giao điểm của IA’ với mặt phẳng (AB’C’).
c) Tìm giao tuyến của (AB’C’) và (A’BC).
Giải:
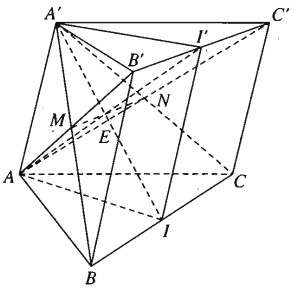
a) Ta có II′∥BB′ và II’ = BB’
Mặt khác AA′∥BB′ và AA’ = BB’ nên:
AA′∥II′ và AA’ = II’
⇒ AA’II’ là hình bình hành.
⇒AI∥A′I′
b) Ta có:
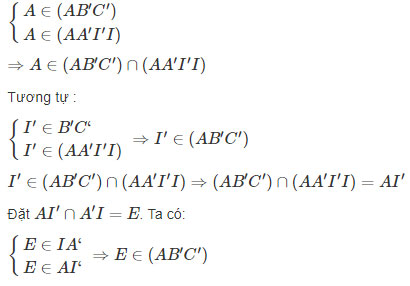
Vậy E là giao điểm của AI’ và mặt phẳng (AB’C’)
c) Ta có:
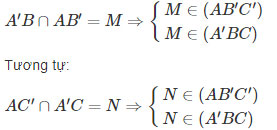
Vậy (AB′C′)∩(A′BC)=MN
Bài 2.26 trang 80 Sách bài tập (SBT) Hình học 11
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi H là trung điểm của A’B’.
a) Chứng minh rằng CB′∥(AHC′)
b) Tìm giao tuyến d của (AB’C’) và (ABC)
Giải:
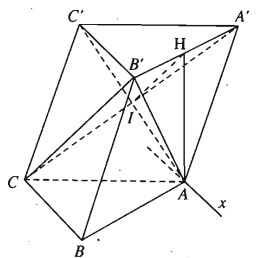
a) Ta có tứ giác AA’CC’ là hình bình hành suy ra A’C cắt AC’ tại trung điểm I của mỗi đường.
Do đó IH∥CB′ (đường trung bình của tam giác CB’A’)
Mặt khác IH⊂(AHC′) nên CB′∥(AHC′)
b) Ta có:
⇒ A là điểm chung của (AB’C’) và (ABC)
Mà
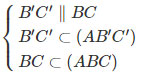
Nên (AB′C′)∩(ABC)=Ax
Và Ax∥BC∥B′C′
Bài 2.27 trang 80 Sách bài tập (SBT) Hình học 11
Cho hai hình bình hành ABCD và ABEF không nằm cùng trong một mặt phẳng. Gọi M và N là hai điểm di động tương ứng trên AD và BE sao cho
AM/MD=BN/NE
Chứng minh rằng đường thẳng MN luôn luôn song song với một mặt phẳng cố định. Hãy chỉ ra mặt phẳng cố định đó.
Giải:
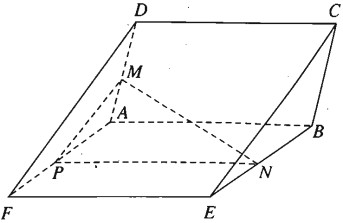
Trong mặt phẳng (ADF), kẻ đường thẳng MP∥DF(P∈AF)
Ta có AP/PF=AM/MD=BN/NE
Nên PN∥FE. Do đó (MNP)∥(DEF).
Vậy MN song song với mặt phẳng (DEF) cố định.
Bài 2.28 trang 80 Sách bài tập (SBT) Hình học 11
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD, O là giao điểm hai đường chéo, AC = a, BD = b, tam giác SBD đều. Gọi I là điểm di động trên đoạn AC với. Lấy là mặt phẳng đi qua I và song song với mặt phẳng (SBD).
a) Xác định thiết diện của mặt phẳng với hình chóp S.ABCD.
b) Tìm diện tích S của thiết diện ở câu a) theo a, b, x. Tìm x để S lớn nhất.
Giải:
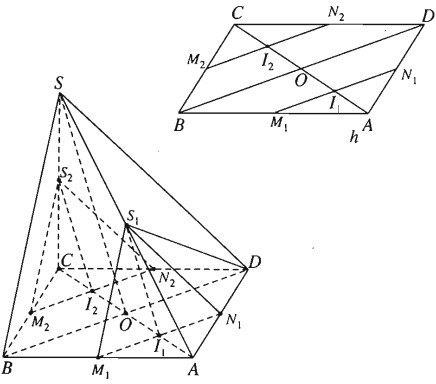
a) Trường hợp 1.
I thuộc đoạn AO(0<x<a/2)
Khi đó I ở vị trí I1
Ta có: (α)∥(SBD)
Vì (α)∥B nên (α) cắt (ABD) theo giao tuyến M1N1 (qua I1) song song với BD
Tương tự (α)∥SO nên (α) cắt (SOA) theo giao tuyến
S1I1 song song với SO.
Ta có thiết diện trong trường hợp này là tam giác S1M1N1.
Nhận xét. Dễ thấy rằng S1M1∥SB và S1N1∥SD. Lúc đó tam giác S1M1N1 đều.
Trường hợp 2. I thuộc đoạn OC(a/2<x<a)
Khi đó I ở vị trí I2. Tương tự như trường hợp 1 ta có thiết diện là tam giác đều S2M2N2 có M2N2∥BD, S2M2∥SB, S2N2∥SD.
Trường hợp 3. I≡O. Thiết diện chính là tam giác đều SBD.
b) Ta lần lượt tìm diện tích thiết diện trong các trường hợp 1,2,3.
Trường hợp 1. I thuộc đoạn AO(0<x<a/2)
\(S_{S_1M_1N_1}\)/SSBD=(M1N1/BD)2=(2x/a)2
\(S_{S_1M_1N_1}\)=4x2/a2.SSBD=4x2/a2.b2√3/4=b2x2√3/a2
Trường hợp 2. I thuộc đoạn OC(a/2<x<a)
\(S_{S_2M_2N_2}\)/SSBD=(M2N2/BD)2=[2(a−x)2/a]
\(S_{S_2M_2N_2}\)=4/a2(a−x)2.b2√3/4=b2√3/a2(a−x)2
Trường hợp 3. I≡O
SSBD=b2√3/4
Tóm lại
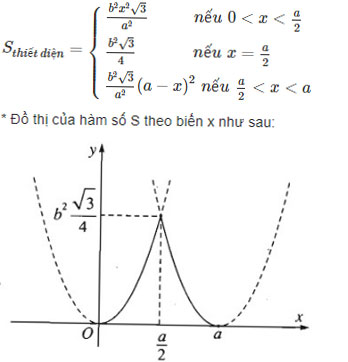
Vậy Sthiết diện lớn nhất khi và chỉ khi x=a/2
Bài 2.29 trang 80 Sách bài tập (SBT) Hình học 11
Cho ba mặt phẳng (α),(β),(γ) song song với nhau. Hai đường thẳng a và a’ cắt ba mặt phẳng ấy theo thứ tự nói trên tại A, B, C vàA’, B’, C’. Cho AB=5,BC=4,A′C′=18. Tính độ dài.A’B’, B’C’
Giải:
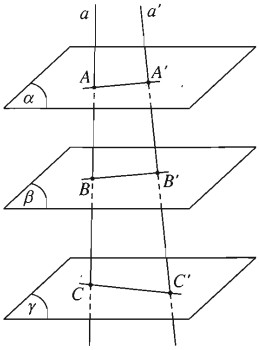
Vì (α)∥(β)∥(γ) nên ABA′B′=BCB′C′
Mặt khác ta có:
AB/A′B′=BC/B′C′=AB+BC/A′B′+B′C′=AC/A′C′
Suy ra: A′B′=A′C′.AB/AC=18.5/9=10
Vậy A’B’ = 10 và B′C′=A′C′.BC/AC=18.4/9=8
Vậy B’C’ = 8.
Bài 2.30 trang 81 Sách bài tập (SBT) Hình học 11
Cho tứ diện ABCD. Gọi I và J lần lượt là hai điểm di động trên các cạnh AD và BC sao cho IAID=JBJC. Chứng minh rằng IJ luôn luôn song song với một mặt phẳng cố định.
Giải:
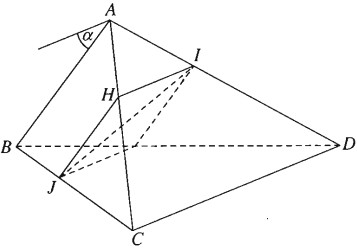
Qua I kẻ đường thẳng song song với CD cắt AC tại H, ta có:
HAHC=IAID
Mặt khác IAID=JBJC
Nên HAHC=JBJC
Suy ra HJ∥AB
Như vậy mặt phẳng (IJH) song song với AB và CD.
Gọi (α) là mặt phẳng qua AB và song song với CD, ta có
Vậy IJ song song với mặt phẳng (α) cố định.
Bài 2.31 trang 81 Sách bài tập (SBT) Hình học 11
Cho hai tia Ax, By chéo nhau. Lấy M, N lần lượt là các điểm di động trên Ax, By. Gọi (α) là mặt phẳng chứa By và song song với Ax. Đường thẳng qua M và song song với AB cắt (α) tại M’.
a) Tìm tập hợp điểm M’.
b) Gọi I là trung điểm của MN. Tìm tập hợp các điểm I khi AM = BN
Giải:
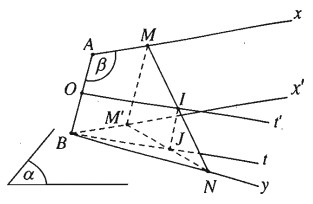
a) Gọi (β) là mặt phẳng xác định bởi hai đường thẳng AB và Ax
Do Ax∥(α) nên (β) sẽ cắt (α) theo giao tuyến Bx’ song song với Ax.
Ta có M’ là điểm chung của (α) và (β) nên M’ thuộc Bx’.
Khi M trùng A thì M’ trùng B nên tập hợp M’ là tia Bx’.
Ta có tứ giác ABM’M là hình bình hành nên BM’ = AM = BN.
Tam giác BM’N cân tại B.
Suy ra trung điểm I của cạnh đáy NM’ thuộc phân giác trong Bt của góc B trong tam giác cân BNM’. Dễ thấy rằng Bt cố định.
Gọi O là trung điểm của AB. Trong mặt phẳng (AB, Bt), tứ giác OBIJ là hình bình hành nên JI→=BO→. Do đó I là ảnh của J trong phép tịnh tiến theo vectơ BO→. Vậy tập hợp I là tia Ot’ song song với Bt.
-----------------------------------
Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải SBT Toán 11 bài 4: Hai mặt phẳng song song. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Sinh học lớp 11, Vật lý lớp 11, Hóa học lớp 11, Giải bài tập Toán 11 mà VnDoc tổng hợp và đăng tải.
