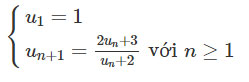Giải SBT Toán 11 ôn tập chương 4: Giới hạn

Toán 11 - Giới hạn

Để giúp các bạn học sinh có kết quả cao hơn trong học tập, VnDoc mời các bạn tham khảo tài liệu Giải SBT Toán 11 ôn tập chương 4: Giới hạn, với nội dung được cập nhật chi tiết và chính xác nhất. Mời các bạn và thầy cô cùng tham khảo.

Giải SBT Toán 11 ôn tập chương 4

Bài 1 trang 170 Sách bài tập (SBT) Đại số 11 và giải tích 11

Tính các giới hạn sau

a) lim(−3)ⁿ+2.5ⁿ/1−5ⁿ

b) lim1+2+3+...+n/n²+n+1

c) lim\(\left(\sqrt{n^2+2n+1}-\sqrt{n^2+n-1}\right)\)

Giải:

a) - 2;

b) 1/2;

c) 1/2

Bài 2 trang 170 Sách bài tập (SBT) Đại số và giải tích 11

Tìm giới hạn của dãy số (u_n) với

a) un=(−1)ⁿ/n²+1

b) u_n=2ⁿ−n/3ⁿ+1

Giải:

a) Ta có, |u_n|=∣(−1)ⁿ/n²+1∣=1/n²+1. Đặt v_n=1/n²+1 (1)

Ta có limv_n=lim1/n²+1=lim\(\frac{\frac{1}{n^2}}{1+\frac{1}{n^2}}=0\)

Do đó, |v_n| có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi.

Từ (1) suy ra, |u_n|=v_n=|v_n|

Vậy, |u_n| cũng có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi, nghĩa là limu_n=0

b) Hướng dẫn: |u_n|=∣2ⁿ−n/3ⁿ+1∣<2ⁿ/3ⁿ+1

Bài 3 trang 170 Sách bài tập (SBT) Đại số và giải tích 11

Viết số thập phân vô hạn tuần hoàn 2,131131131… (chu kì 131) dưới dạng phân số.

Giải:

2,131131131...=2+131/1000+131/1000²+...+131/1000ⁿ+...

=2+\(\frac{\frac{131}{1000}}{1-\frac{1}{1000}}\)

=2+131/999=2129/999

(Vì 131/1000,131/1000²,...,131/1000ⁿ, ... là một cấp số nhân lùi vô hạn với công bội q=1/1000).

Bài 4 trang 171 Sách bài tập (SBT) Đại số và giải tích 11

Cho dãy số (u_n) xác định bởi

a) Chứng minh rằng u_n>0 với mọi n.

b) Biết (u_n) có giới hạn hữu hạn. Tìm giới hạn đó.

Giải:

a) Chứng minh bằng quy nạp: u_n>0 với mọi n. (1)

- Với n = 1 ta có u₁=1>0

- Giả sử (1) đúng với n=k≥1 nghĩa là u_k>0 ta cần chứng minh (1) đúng với n = k + 1

Ta có uk+1=2u_k+3/u_k+2. Vì u_k>0 nên u_k+1=2u_k+3/u_k+2>0

- Kết luận: u_n>0 với mọi n.

b) Đặt

limu_n=a

u_n+1=2u_n+3/u_n+2

⇒limu_n+1=lim2u_n+3/u_n+2

⇒a=2a+3/a+2⇒a=±√3

Vì u_n>0 với mọi n, nên limu_n=a≥0. Từ đó suy ra limu_n=√3

Bài 5 trang 171 Sách bài tập (SBT) Đại số và giải tích 11

Cho dãy số (u_n) thoả mãn u_n<M với mọi n. Chứng minh rằng nếu limu_n=a thì a≤M

Giải:

Xét dãy số (v_n) với v_n=M−u_n

u_n<M với mọi n ⇒v_n>0 với mọi n. (1)

Mặt khác, limv_n=lim(M−u_n)=M−a (2)

Từ (1) và (2) suy ra M−a≥0 hay a≤M

Bài 6 trang 171 Sách bài tập (SBT) Đại số và giải tích 11

Từ độ cao 63m của tháp nghiêng PISA ở Italia (H.5) người ta thả một quả bóng cao su xuống đất. Giả sử mỗi lần chạm đất quả bóng lại nảy lên một độ cao bằng 1/10 độ cao mà quả bóng đạt được ngay trước đó.

Tính độ dài hành trình của quả bóng từ thời điểm ban đầu cho đến khi nó nằm yên trên mặt đất.

Giải:

Mỗi khi chạm đất quả bóng lại nảy lên một độ cao bằng 1/10 độ cao của lần rơi ngay trước đó và sau đó lại rơi xuống từ độ cao thứ hai này. Do đó, độ dài hành trình của quả bóng kể từ thời điểm rơi ban đầu đến:

- thời điểm chạm đất lần thứ nhất là d₁=63

- thời điểm chạm đất lần thứ hai là d₂=63+2.63/10

- thời điểm chạm đất lần thứ ba là d₃=63+2.63/10+2.63/10²

- thời điểm chạm đất lần thứ tư là d₄=63+2.63/10+2.63/10²+2.63/10³

…

- thời điểm chạm đất lần thứ n (n > 1) là

d_n=63+2.63/10+2.63/10²+...+2.63/10ⁿ⁻¹

(Có thể chứng minh khẳng định này bằng quy nạp).

Do đó, độ dài hành trình của quả bóng kể từ thời điểm rơi ban đầu đến khi nằm yên trên mặt đất là:

d=63+2.63/10+2.63/10²+...+2.6310ⁿ⁻¹+... (mét).

Vì 2.63/10,2.63/10²,...,2.63/10ⁿ⁻¹.... là một cấp số nhân lùi vô hạn, công bội q=1/10 nên ta có:

2.63/10+2.63/10²+...+2.63/10ⁿ⁻¹+...\(\frac{2\frac{63}{10}}{1-\frac{1}{10}}=14\)

Vậy, d=63+2.63/10+2.63/10²+...+2.63/10ⁿ⁻¹+...=63+14=77 (mét).

Bài 7 trang 171 Sách bài tập (SBT) Đại số và giải tích 11

Chứng minh rằng hàm số f(x)=cos1/x không có giới hạn khi x→0

Giải:

Hướng dẫn: Chọn hai dãy số có số hạng tổng quát là an=1/2nπ và bn=1/(2n+1)π. Tính và so sánh limf(a_n) và limf(b_n) để kết luận về giới hạn của f(x) khi x→0

Bài 8 trang 171 Sách bài tập (SBT) Đại số và giải tích 11

Tìm các giới hạn sau:

a) lim_x→−2x+5/x²+x−3

b) lim_{x→3−\(\sqrt{x^2+8x+3}\)}

c) lim_x→+∞(x³+2x²√x−1)

d) lim_x→−12x³−5x−4/(x+1)²

Giải:

a) -3

b) 6

c) + ∞

d) - ∞

Bài 9 trang 171 Sách bài tập (SBT) Đại số và giải tích 11

Tìm các giới hạn sau:

a) lim_{x→0\(\frac{\sqrt{x^2+1}-1}{\sqrt{x^2+16}}\)}

b) lim_x→1x−√x/\(\sqrt{x-1}\)

c) lim_x→+∞2x⁴+5x−1/1−x²+x⁴

d) lim_{x→−∞\(\frac{x+\sqrt{4x^2-x+1}}{1-x}\)}

e) lim_x→+∞x(\(\sqrt{x^2+1}\)−x)

f) lim_x→2+(1/x²−4−1/x−2)

Giải:

a) 4;

b) 1;

c) 2;

d) 1/2

e)

lim_x→+∞x(\(\sqrt{x^2+1}\)−x)

=lim_x→+∞x(x²+1−x²)/\(\sqrt{x^2+1}+x\)=lim_x→+∞x/x\(\sqrt{1+\frac{1}{x^2}}\)+x

=lim_x→+∞1/\(\sqrt{1+\frac{1}{x^2}}\)+1=1/2

f)

lim^x→2+(1/x²−4−1/x−2)

=lim_x→2+1−(x+2)/x²−4

=lim_x→2+−x−1/x²−4=−∞

Bài 10 trang 172 Sách bài tập (SBT) Đại số và giải tích 11

Xác định một hàm số y=f(x) thoả mãn đồng thời các điều kiện sau:

a) f(x) xác định trên R\ {1},

b) lim_x→1f(x)=+∞;lim_x→+∞f(x)=2 và lim_x→−∞f(x)=2

Giải:

Chẳng hạn f(x)=2x²+1/(x−1)². Dễ dàng kiểm tra được rằng f(x) thoả mãn các điều kiện đã nêu.

-----------------------------------

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải SBT Toán 11 ôn tập chương 4: Giới hạn. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Sinh học lớp 11, Vật lý lớp 11, Hóa học lớp 11, Giải bài tập Toán 11 mà VnDoc tổng hợp và đăng tải.