Đề thi chọn học sinh giỏi Quốc gia THPT năm 2014
|
BỘ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ THI CHÍNH THỨC |
KỲ THI CHỌN HỌC SINH GIỎI QUỐC GIA THPT NĂM 2014 |
ĐỀ THI MÔN: TOÁN
Thời gian: 180 phút (không kể thời gian giao đề)
Ngày thi thứ nhất: 03/01/2014
Bài 1 (5.0 điểm).
Cho hai dãy số dương (xn), (yn) xác định bởi x1 = 1, y1 = √3 và![]()
với mọi n = 1, 2... Chứng minh rằng hai dãy số trên hội tụ và tìm giới hạn của chúng.
Bài 2 (5.0 điểm).
Cho đa thức P(x) = (x2 - 7x + 6)2n với n là số nguyên dương. Chứng minh rằng P(x) không thể biểu diễn được dưới dạng tích của n + 1 đa thức khác hằng số với hệ số nguyên.
Bài 3 (5.0 điểm).
Cho đa giác đều có 103 cạnh. Tô màu đỏ 79 đỉnh của đa giác và tô màu xanh các đỉnh còn lại. Gọi A là số cặp đỉnh đỏ kề nhau và B là số cặp đỉnh xanh kề nhau.
1. Tìm tất cả các giá trị có thể nhận được của cặp (A, B).
2. Xác định số cách tô màu các đỉnh của đa giác để B = 14. Biết rằng, hai cách tô màu được xem là như nhau nếu chúng có thể nhận được từ nhau qua một phép quay quanh tâm đường tròn ngoại tiếp đa giác.
Bài 4 (5.0 điểm).
Cho tam giác nhọn ABC nội tiếp đường tròn (O) với AB < AC. Gọi I là trung điểm cung BC không chứa A. Trên AC lấy điểm K khác C sao cho IK = IC. Đường thẳng BK cắt (O) tại D (D # B) và cắt đường thẳng AI tại E. Đường thẳng DI cắt đường thẳng AC tại F.
1. Chứng minh rằng EF = BC/2.
2. Trên DI lấy điểm M sao cho CM song song với AD. Đường thẳng KM cắt đường thẳng BC tại N. Đường tròn ngoại tiếp tam giác BNK cắt (O) tại P (P # B). Chứng minh rằng đường thẳng PK đi qua trung điểm đoạn thẳng AD.
ĐỀ THI MÔN: TOÁN
Thời gian: 180 phút (không kể thời gian giao đề)
Ngày thi thứ hai: 04/01/2014
Bài 5 (7.0 điểm).
Cho tam giác nhọn ABC nội tiếp đường tròn (O), trong đó B, C cố định và A thay đổi trên (O). Trên các tia AB và AC lần lượt lấy các điểm M và N sao cho MA = MC và NA = NB. Các đường tròn ngoại tiếp các tam giác AMN và ABC cắt nhau tại P (P # A). Đường thẳng MN cắt đường thẳng BC tại Q.
1. Chứng minh rằng ba điểm A, P, Q thẳng hàng.
2. Gọi D là trung điểm BC. Các đường tròn có tâm là M, N cùng đi qua A cắt nhau tại K (K # A). Đường thẳng qua A vuông góc với AK cắt BC tại E. Đường tròn ngoại tiếp tam giác ADE cắt (O) tại F (F # A). Chứng minh rằng đường thẳng AF đi qua một điểm cố định.
Bài 6 (7.0 điểm). Tìm giá trị lớn nhất của biểu thức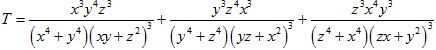
với x, y, z là các số thực dương.
Bài 7 (6.0 điểm).
Tìm tất cả các bộ số gồm 2014 số hữu tỉ không nhất thiết phân biệt, thỏa mãn điều kiện: nếu bỏ đi một số bất kì trong bộ số đó thì 2013 số còn lại có thể chia thành 3 nhóm rời nhau sao cho mỗi nhóm gồm 671 số và tích tất cả các số trong mỗi nhóm bằng nhau.

