Đề thi học sinh giỏi giải toán trên Máy tính cầm tay tỉnh Thừa Thiên Huế - Khối 12 hệ bổ túc (2009 - 2010)

SỞ GIÁO DỤC VÀ ĐÀO TẠO THỪA THIÊN HUẾ (Đề thi chính thức)

KỲ THI CHỌN HỌC SINH GIỎI TỈNH GIẢI TOÁN TRÊN MÁY TÍNH CẦM TAY KHỐI 12 BTTHPT - NĂM HỌC 2009 - 2010 (Thời gian làm bài 150 phút không kể thời gian giao đề) Ngày thi: 20/12/2009

Qui định: Học sinh trình bày vắn tắt cách giải, công thức áp dụng, kết quả tính toán vào ô trống liền kề bài toán. Các kết quả tính gần đúng, nếu không có chỉ định cụ thể, được ngầm định chính xác tới 4 chữ số phần thập phân sau dấu phẩy

Bài 1. (5 điểm)

Tính gần đúng nghiệm (độ, phút, giây) của phương trình 3cos2x + 5sinxcosx = 2.

Bài 2. (5 điểm)

Tính gần đúng giá trị lớn nhất và giá trị nhỏ nhất của hàm số:

Bài 3. (5 điểm)

Tính gần đúng giá trị cực tiểu và giá trị cực đại của hàm số:

Bài 4. (5 điểm)

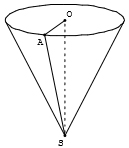
Khi sản xuất cái phểu hình nón (không có nắp) bằng nhôm, các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nguyên liệu làm phểu là ít nhất, tức là diện tích xung quanh của hình nón là nhỏ nhất. Tính gần đúng diện tích xung quanh của phểu khi ta muốn có thể tích của phểu là 1 dm³

Bài 5. (5 điểm)

Tính gần đúng nghiệm của hệ phương trình: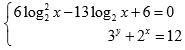

Bài 6. (5 điểm)

Đa thức P(x) = x⁴ + ax³ + bx² + cx + d có giá trị là 8; 0; -4; -4 khi x lần lượt nhận giá trị là 1; 2; 3; 4.

a) Xác định các hệ số a, b, c, d của đa thức P(x).

b) Tính chính xác các giá trị của P(x) ứng với các giá trị của x = 15; 27; 159; 2009

Bài 7. (5 điểm)

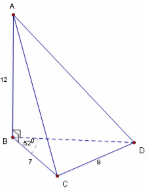
Cho tứ diện ABCD có AB = 12dm; AB vuông góc với mặt phẳng (BCD); BC = 7dm; CD = 9dm và góc CBD = 520. Tính gần đúng thể tích và diện tích toàn phần của tứ diện ABCD

Bài 8. (5 điểm)

Cho dãy hai số u_n xác định bởi:

a. Tính các giá trị chính xác của u₂, u₃, u₄, u₅, u₁₀, u₁₁, u₁₂, u₁₃.

b. Từ đó dự đoán rằng dãy số luôn luôn nhận giá trị nguyên. Hãy thiết lập công thức truy hồi để tính u_n+2 theo u_n+1 và u_n

Bài 9. (5 điểm)

Tìm giá trị gần đúng của a và b để đường thẳng y = ax + b là tiếp tuyến của đồ thị (C) của hàm số tại điểm (C) có hoành độ x_o = -2.

Bài 10. (5 điểm)

Tính gần đúng tọa độ các giao điểm của đường tròn có tâm I(3; 0), bán kính R = 4 và đường elip