Đề thi học sinh giỏi lớp 12 Bổ túc THPT môn Toán tỉnh Thanh Hóa năm 2013 - 2014

Đề thi học sinh giỏi cấp Tỉnh môn Toán

Đề thi học sinh giỏi lớp 12 Bổ túc THPT môn Toán tỉnh Thanh Hóa năm 2013 - 2014 là đề thi học sinh giỏi tỉnh Thanh Hóa có đáp án dành cho các bạn tham khảo luyện đề học sinh giỏi. Mời các bạn tham khảo.

Đề thi học sinh giỏi lớp 12

SỞ GIÁO DỤC VÀ ĐÀO TẠO THANH HÓA

ĐỀ CHÍNH THỨC

KỲ THI HỌC SINH GIỎI CẤP TỈNH
Năm học 2013 – 2014
Môn thi: TOÁN
Lớp 12 BỔ TÚC THPT
Ngày thi: 21/03/2014
Thời gian: 180 phút (Không kể thời gian giao đề)
Đề thi này có 01 trang, gồm có 5 câu

Câu I (4,0 điểm).

Cho hàm số y = (2 - m)x³ - 6mx² + 9(2 - m)x - 2 có đồ thị (C_m).

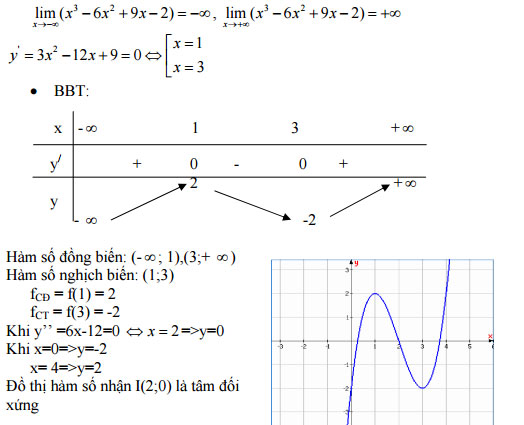
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số trên với m = 1.

2. Tìm m để đường thẳng d: y = - 2 cắt (C_m) tại ba điểm phân biệt A(0; -2), B và C sao cho diện tích tam giác OBC bằng √13.

Câu II (4,0 điểm)

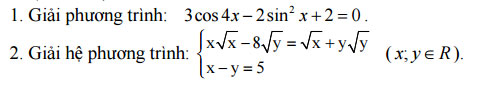
Câu III (4,0 điểm).

1. Cho 6 số thực a, b, c, m, n, p thỏa mãn: a² + b² + c² = 1 và m + n + p = 5. Tìm giá trị lớn nhất của biểu thức:

T = a.m + b.n + c.p + m.n + n.p + p.m.

2. Giải phương trình log₄(x+1)² + 2 = log_√2√(4-x) + log₈(4+x)³

Câu IV (4,0 điểm).

1. Tìm hệ số của số hạng chứa 8 x trong khai triển nhị thức Niutơn của (x² + 2)ⁿ, biết:

2. Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): 3x – 4y + 25 = 0 và đường thẳng (d'): 15x + 8y – 41 = 0. Gọi I là giao điểm của (d) và (d'). Viết phương trình đường thẳng đi qua I và tạo với trục hoành một góc bằng 60^o.

Câu V (4,0 điểm).

1. Đáy ABCD của hình chóp S.ABCD là hình thoi với cạnh AB = a, góc BAD = 60^o. Các cạnh bên SA = SC, SB = SD = a.

a/ Tính thể tích của khối chóp đã cho.

b/ Gọi M là trung điểm của cạnh SC. Tính giá trị cos BMD.

2. Trong không gian với hệ toạ độ Oxyz, cho bốn điểm A(1;1;1), B(2;0;6), C(3;2;0) , D(7;4;2). Lập phương trình mặt phẳng (P) đi qua A, B và cách đều C, D.

………………………………..HẾT…………………………………….

Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.