Đề thi thử đại học năm 2014 trường THPT chuyên Lương Văn Chánh

Đề thi thử tuyển sinh đại học môn Toán

I. PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7,0 điểm)

Câu I (2,0 điểm). Cho hàm số y = x³ – 3x² + (m – 2)x + 3m (C_m) (m là tham số).

1. Khảo sát và vẽ đồ thị hàm số ứng với m = 2.

2. Tìm m để tiếp tuyến có hệ số góc nhỏ nhất của đồ thị (C_m) của hàm số đã cho vuông góc với đường thẳng (d): x – y + 2 = 0 .

Câu II (2,0 điểm)

1. Giải phương trình:

2. Tính:

Câu III (1,0 điểm) Giải hệ phương trình: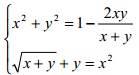

Câu IV (1,0 điểm)

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và cạnh bên bằng . Điểm M là trung điểm của cạnh SA. Tính thể tích tứ diện SMBD.

Câu V (1,0 điểm) Cho a, b, c là ba số thực dương thỏa mãn abc = 1. Chứng minh rằng:

II. PHẦN RIÊNG (3,0 điểm).

Câu VIa (3,0 điểm). DÀNH CHO THÍ SINH THI KHỐI: A, A1, B

1.a) Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d₁: 2x + 2y – 1 = 0; d₂: 4x – √2 y + 3 = 0. Gọi A là giao điểm của d₁ và d₂. Viết phương trình đường thẳng qua M (4; -2) và lần lượt cắt d₁, d₂ tại B, C sao cho tam giác ABC cân tại A.

2.a) Một tổ học sinh có 4 em Nữ và 5 em Nam được xếp thành một hàng dọc. Tính xác suất để chỉ có hai em nữ A , B đứng cạnh nhau còn các em nữ còn lại không đứng cạnh nhau và cũng không đứng cạnh A, B.

3.a) Tìm m để bất phương trình sau có nghiệm thuộc đoạn [0; 1 + √3]

Câu VIb (3điểm). DÀNH CHO THÍ SINH THI KHỐI: D, D1, M

1.b) Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x² + y² – 4x – 2y – 4 = 0. Viết phương trình đường thẳng qua M(1; 4) và tiếp xúc với đường tròn (C).

2.b) Tìm hệ số của x¹⁰ trong khai triển Niu tơn đa thức với n là số tự nhiên thỏa mãn:

3.b) Xác định m để bất phương trình: 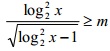nghiệm đúng với mọi x thuộc tập xác định