Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Chuyên Nguyễn Đình Chiểu

Đề thi thử THPT Quốc gia môn Toán

Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Chuyên Nguyễn Đình Chiểu là đề thi thử có chất lượng được VnDoc.com sưu tầm và đăng tải. Đề thi có đáp án, mời các bạn tham khảo và củng cố kiến thức, chuẩn bị cho kì thi THPT Quốc gia sắp tới. Mời các bạn cùng tham khảo.

Tuyển tập 20 đề thi thử THPT Quốc gia môn Toán năm 2016

Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Hậu Lộc 2, Thanh Hóa

Câu 1: (2,0 điểm) Cho hàm số (C)

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.

b) Cho hai điểm A(1; 0) và B(-7; 4). Viết phương trình tiếp tuyến của (C), biết tiếp tuyến đi qua điểm trung điểm I của AB.

Câu 2: (1,0 điểm)

a) Cho α - β = π/6. Tính giá trị

b) Giải phương trình (2sinx + 3cosx)² + (3sinx + 2cosx)² = 25.

Câu 3: (1,0 điểm)

a) Cho hàm số y = x.lnx - 2x. Giải phương trình y' = 0.

b) Giải hệ phương trình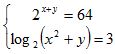

Câu 4: (1,0 điểm) Cho hàm số f(x) = tanx(2cotx - √2cosx + 2cos²x) có nguyên hàm là F(x) và F(π/4) = π/2. Tìm nguyên hàm F(x) của hàm số đã cho.

Câu 5: (1,0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Biết SA ⊥ ABCD, SC hợp với mặt phẳng (ABCD) một góc α với tanα = 4/5, AB = 3a và BC = 4a. Tính thể tích của khối chóp S.ABCD và khoảng cách từ điểm đến D mặt phẳng (SBC).

Câu 6: (1,0 điểm) Trong không gian Oxyz cho các điểm A(3; -4; 0), B(0; 2; 4), C(4; 2; 1). Tính diện tích tam giác ABD và tìm tọa độ điểm D trên trục Ox sao cho AD = BC.

Câu 7 (1,0 điểm) Trong mặt phẳng toạ độ Oxy cho đường tròn (C₁): (x - 1)² + (y - 1)² = 4 có tâm là I₁ và đường tròn (C₂): (x - 4)² + (y - 4)² = 10 có tâm là I₂, biết hai đường tròn cắt nhau tại A và B. Tìm tọa độ điểm M trên đường thẳng AB sao cho diện tích tam giác MI₁I₂ bằng 6.

Câu 8 (1,0 điểm) Giải phương trình .

Câu 9: (1,0 điểm) Cho x≥ 0 và y ≥ 0 thỏa điều kiện x + y = 2. Tìm giá trị lớn nhất của biểu thức

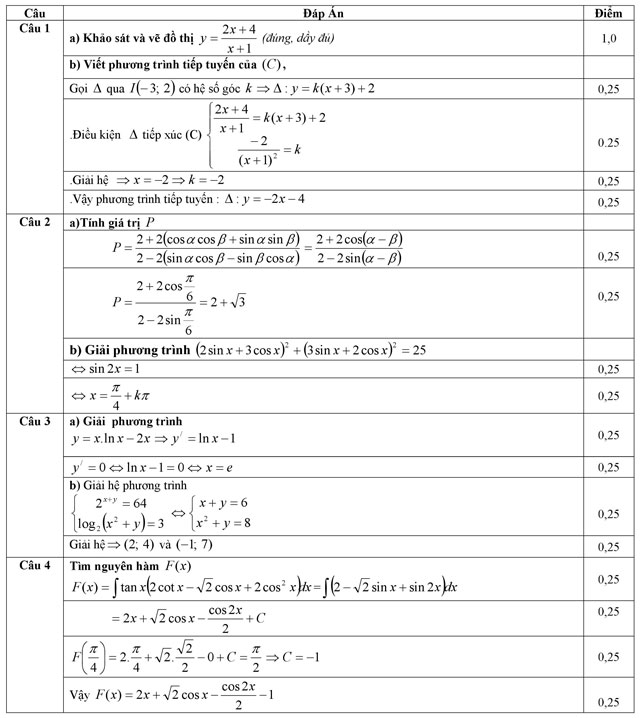
Đáp án đề thi thử THPT Quốc gia môn Toán