Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Hậu Lộc 2, Thanh Hóa

Đề thi thử THPT Quốc gia môn Toán

Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Hậu Lộc 2, Thanh Hóa là tài liệu hữu ích dành cho ôn thi tốt nghiệp, ôn thi THPT Quốc gia, ôn thi đại học môn Toán. Tài liệu này gồm đề thi và đáp án kèm theo, giúp các bạn dễ dàng luyện tập và kiểm tra kết quả. Mời các bạn tải về để tham khảo.

Đề thi thử Quốc gia lần 1 năm 2015 môn Toán trường THPT Hậu Lộc 2, Thanh Hóa

Tuyển tập 20 đề thi thử THPT Quốc gia môn Toán năm 2016

Đề thi thử Quốc gia lần 2 năm 2015 môn Toán trường THPT Hậu Lộc 2, Thanh Hóa

SỞ GD&ĐT THANH HÓA TRƯỜNG THPT HẬU LỘC 2 (Đề thi gồm 01 trang)

KÌ THI THỬ THPT QUỐC GIA NĂM 2016-LẦN 1 Môn thi: TOÁN Thời gian làm bài: 180 phút không kể thời gian phát đề.

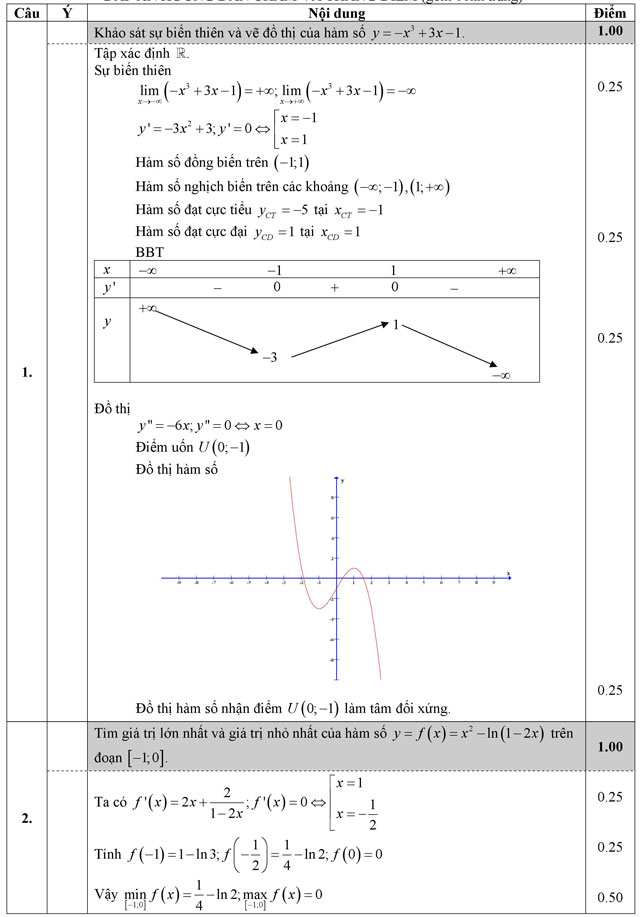
Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = -x³ + 3x - 1.

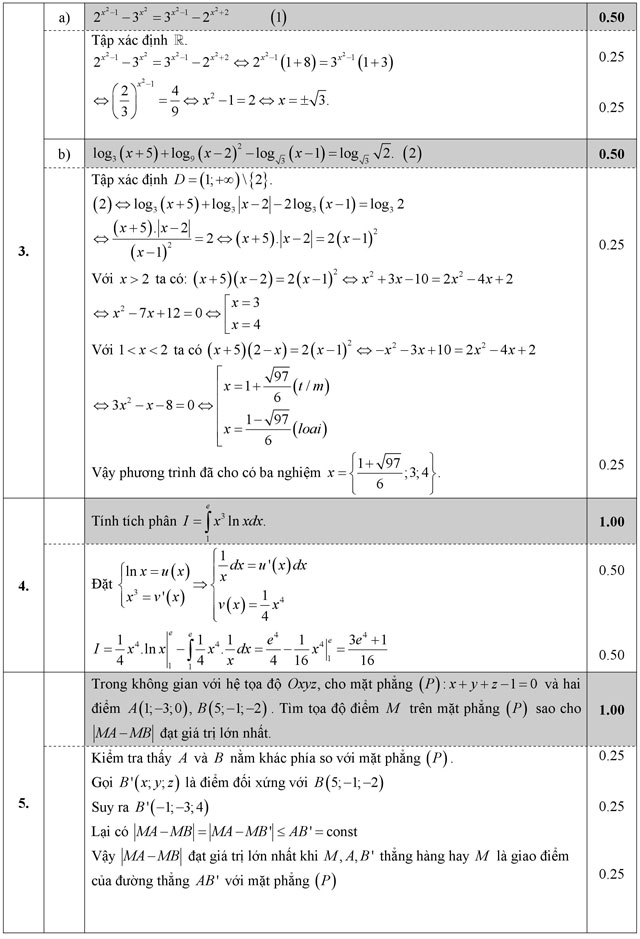
Câu 2 (1,0 điểm). Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) = x² - ln(1 - 2x) trên đoạn [-1; 0].

Câu 3 (1,0 điểm). Giải các phương trình sau:

b) log₃(x + 5) + log₉(x - 2)² - log_√3(x - 1) = log_√3√2.

Câu 4 (1,0 điểm). Tính tích phân

Câu 5 (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + y + z - 1 = 0 và hai điểm A(1; -3; 0), B(5; -1; -2). Tìm tọa độ điểm M trên mặt phẳng (P) sao cho |MA- MB| đạt giá trị lớn nhất.

Câu 6 (1,0 điểm).

a) Giải phương trình 2√3cos²x + 6sinx.cosx = 3 + √3.

b) Có 30 tấm thẻ đánh số từ 1 đến 30. Chọn ngẫu nhiên ra 10 tấm thẻ. Tìm xác suất để có 5 tấm thẻ mang số lẻ, 5 tấm thẻ mang số chẵn, trong đó chỉ có đúng 1 tấm thẻ mang số chia hết cho 10.

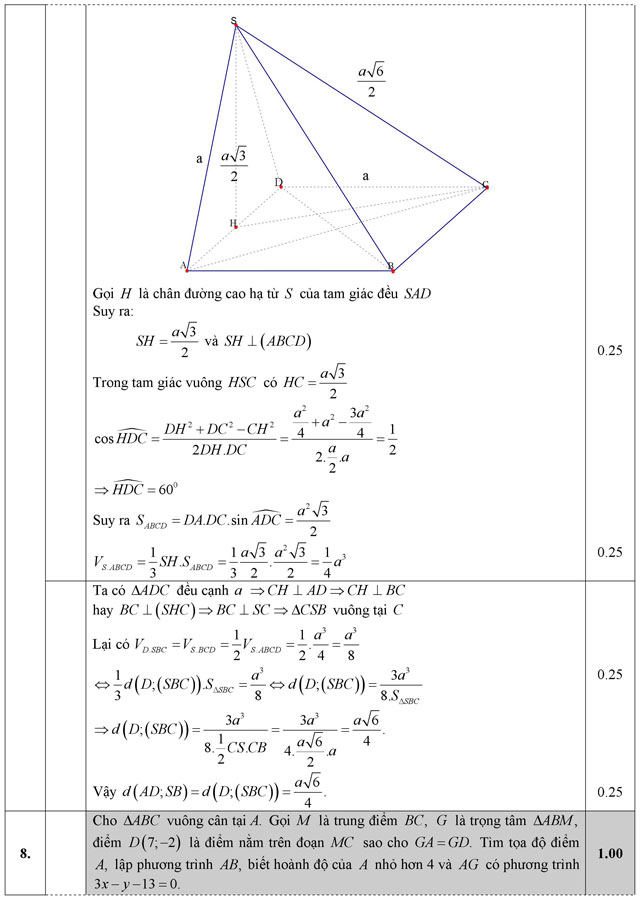
Câu 7 (1,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, mặt bên SAD là tam giác đều nằm trong mặt phẳng vuông góc với đáy, SC = a√6/2. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AD, SB theo a.

Câu 8 (1,0 điểm). Cho ΔABC vuông cân tại A. Gọi M là trung điểm BC, G là trọng tâm ΔABM, điểm D(7; -2) là điểm nằm trên đoạn MC sao cho GA = GD. Tìm tọa độ điểm A, lập phương trình AB, biết hoành độ của A nhỏ hơn 4 và AG có phương trình 3x - y - 13 = 0.

Câu 9 (1,0 điểm). Giải hệ phương trình

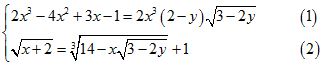
Câu 10 (1,0 điểm). Cho a, b, c là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức:

Đáp án đề thi thử THPT Quốc gia môn Toán