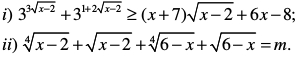Đề thi thử THPT Quốc gia năm 2016 môn Toán tỉnh Phú Thọ
Đề thi thử THPT Quốc gia 2016 môn Toán tỉnh Phú Thọ
Nhằm giúp các bạn học sinh luyện thi THPT Quốc gia môn Toán một cách hiệu quả, VnDoc.com liên tục sưu tầm những đề thi hay của các trường, các Sở GD&ĐT trên cả nước để các bạn có được những đề thi hay và ôn tập hiệu quả. Mời các bạn thử sức với đề thi thử THPT Quốc gia năm 2016 môn Toán tỉnh Phú Thọ.
Đề thi thử THPT Quốc gia môn Toán năm 2016 Sở GD-ĐT Hà Nội
222 đề thi thử THPT Quốc gia môn Toán năm 2016 của các trường THPT trên toàn quốc
SỞ GD & ĐT PHÚ THỌ ĐỀ THI CHÍNH THỨC (Đề thi có 01 trang) | ĐỀ THI THỬ THPT QUỐC GIA Môn thi: TOÁN. Năm học 2015 - 2016 Thời gian: 180 phút, không kể thời gian phát đề. |
Câu 1 (2,0 điểm). Cho hàm số 
a) Khảo sát và vẽ đồ thị hàm số (1).
b) Viết phương trình tiếp tuyến của đồ thị hàm số (1) tại điểm có hoành độ bằng −2.
Câu 2 (1,0 điểm).
a) Giải phương trình: log2x + log4x = 6.
b) Cho số phức z thỏa mãn iz + 2 − i = 0. Tìm điểm biểu diễn của z trên mặt phẳng tọa độ Oxyz.
Câu 3 (1,0 điểm). Tính tích phân: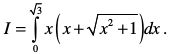
Câu 4 (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x – y + z +3 = 0 và điểm A (1; -2; 1). Tính khoảng cách từ A đến mặt phẳng (P). Viết phương trình đường thẳng ∆ đi qua A và vuông góc với mặt phẳng (P).
Câu 5 (1,0 điểm).
a) Tính giá trị của biểu thức: 
biết cos2x = 0.
b) Một người gọi điện thoại quên ba chữ số cuối cùng của số điệ n thoại cần gọi. Người này chỉ nhớ rằng ba chữ số đều khác nhau và trong đó chắc chắn có một chữ số 9. Tính xác suất để người gọi điện bấm số một lần đúng được số điện thoại cần gọi.
Câu 6 (1,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, 
, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy, góc giữa SD và mặt đáy bằng 60o. Tính theo a thể tích của khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AC, SD.
Câu 7 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC vuông tại A, AC = 2AB. Gọi H là chân đường cao kẻ từ A; các điểm M, N lần lượt là trung điểm của HB và HC. Đường thẳng BC có phương trình x − y − 3 = 0 và trực tâm của tam giác AMN là K (1;0). Tìm tọa độ các điểm A, B, C.
Câu 8 (1,0 điểm). Một người mới đi làm muốn gửi tiền tiết kiệm để mau xe máy. Người đó muốn gửi vào ngân hàng mỗi tháng một số tiền như nhau trong 15 tháng theo thể thức lãi kép (tức là nếu đến kì hạn người gửi không rút lãi ra thì tiền lãi được nhập vào vốn của kì kế tiếp) để được số tiền là 21 triệu đồng vừa đủ mua xe máy. Giả sử lãi suất gửi vào ngân hàng là 0, 07% /tháng, hỏi mỗi tháng người đó cần gửi vào ngân hàng bao nhiêu tiền?
Câu 9 (1,0 điểm). Chứng minh rằng với mọi giá trị m thỏa mãn 2 + 2 ≤ m < 24√2 + 2√2, luôn có đúng 2 số thực x thỏa mãn đồng thời các điều kiện:
