Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Mai Thúc Loan, Hà Tĩnh (Lần 1)

Đề thi thử THPT Quốc gia 2016 môn Toán

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Mai Thúc Loan, Hà Tĩnh có 10 câu hỏi làm trong thời gian 180 phút. VnDoc.com hy vọng đây là tài liệu hữu ích dành cho các bạn, giúp các bạn luyện tập và nâng cao kỹ năng làm bài môn Toán hiệu quả. Mời các bạn tham khảo.

Bộ công thức Toán lớp 12 ôn thi THPT Quốc gia từ A - Z

8 chuyên đề Toán luyện thi THPT Quốc gia

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Nguyễn Văn Trỗi, Hà Tĩnh

SỞ GD & ĐT HÀ TĨNH TRƯỜNG THPT MAI THÚC LOAN

THI THỬ KỲ THI TRUNG HỌC PHỔ THÔNG QUỐC GIA 2016 Môn thi: TOÁN - Lần 1 Thời gian làm bài: 180 phút, không kể thời gian phát đề

Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị hàm số y = x⁴ - 2x² + 1

Câu 2 (1,0 điểm). Tìm giá trị lớn nhất và nhỏ nhất của hàm số

Câu 3 (1,0 điểm).

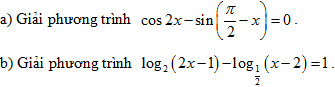
Câu 4 (1,0 điểm). Tính tích phân:

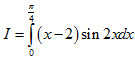
Câu 5 (1,0 điểm). Trong không gian Oxyz, cho các điểm A(-1; 1; 1), B(1; 2; 1), C(1; 1; 2) và D(2; 2; 1).

Viết phương trình mặt phẳng đi qua ba điểm A, B, C và tính khoảng cách từ điểm D đến mặt phẳng (ABC)

Câu 6 (1,0 điểm).

b) Đội dự tuyển học sinh giỏi giải toán trên máy tính cầm tay môn toán của trường THPT Mai Thúc Loan có 4 học sinh nam khối 12, 2 học sinh nữ khối 12 và 2 học sinh nam khối 11. Để thành lập đội tuyển dự thi học sinh giỏi giải toán trên máy tính cầm tay môn toán cấp tỉnh nhà trường cần chọn 5 em từ 8 em học sinh trên. Tính xác suất để trong 5 em được chọn có cả học sinh nam và học sinh nữ, có cả học sinh khối 11 và học sinh khối 12.

Câu 7 (1,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, góc giữa canh bên SD và mặt đáy (ABCD) bằng 45^o. Hình chiếu vuông góc của S lên mặt đáy (ABCD) là điểm H thuộc đoạn BD sao cho HD = 2HB, gọi M là trung điểm AB. Tính theo a thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng SB và CM.

Câu 8 (1,0 điểm). Trong mặt phẳng tọa độ Oxy, cho tam giác ABC nội tiếp đường tròn (C) có phương trình x² + y² + 6x + 2y - 31 = 0. Gọi H (-3;0) và K (2;4) lần lượt là hình chiếu vuông góc của A, C lên BC và AB. Tìm tọa độ các đỉnh của tam giác biết B có hoành độ âm.

Câu 9 (1,0 điểm). Giải hệ phương trình

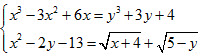
trên tập hợp số thực.

Câu 10 (1,0 điểm). Cho là các số thực thỏa mãn x + y + xyz = xy. Tìm giá trị nhỏ nhất của biểu thức: