Đề thi tuyển sinh lớp 10 THPT tỉnh Bạc Liêu năm học 2010 - 2011 môn Toán (Chuyên) - Có đáp án

Nhằm giúp các bạn chuẩn bị thật tốt kiến thức để làm bài thi đạt hiệu quả cao, Vndoc.com xin giới thiệu: Đề thi tuyển sinh lớp 10 THPT tỉnh Bạc Liêu năm học 2010 - 2011 môn Toán (Chuyên) - Có đáp án.

Đề thi tuyển sinh lớp 10 môn Toán (Chuyên):

SỞ GIÁO DỤC VÀ ĐÀO TẠO BẠC LIÊU (Đề thi chính thức)

KỲ THI TUYỂN SINH LỚP 10 THPT NĂM HỌC: 2010 - 2011

MÔN THI: TOÁN (Chuyên)
Thời gian làm bài 150 phút: (không kể thời gian giao đề)
--------------------------------------------------------------------------------

Câu 1 (2,0 điểm).

Chứng minh rằng n³ + 3n² + 2n chia hết cho 6 với mọi n là số tự nhiên khác 0.

Câu 2 (2,0 điểm).

Cho phương trình: x² - (2m + 3)x + m - 3 = 0 (với m là tham số)

a. Chứng tỏ rằng phương trình luôn có nghiệm với mọi tham số m

b. Gọi x₁, x₂ là các nghiệm của phương trình trên. Tìm m để |x₁ - x₂| đạt giá trị nhỏ nhất. Tính giá trị nhỏ nhất ấy.

Câu 3 (2,0 điểm).

Giải hệ phương trình: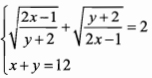

Câu 4 (2,0 điểm).

Cho đường tròn (O; R). Từ một điểm M ở ngoài đường tròn vẽ hai tiếp tuyến MP và MN với đường tròn tâm (O); với P, N là hai tiếp điểm. Vẽ một cát tuyến đi qua M cắt đường tròn tại hai điểm A và B.

a. Chứng minh góc PMO = góc PNO

b. Chứng minh đường tròn ngoại tiếp tam giác MNP đi qua hai điểm có định khi M di chuyển trên cát tuyến trên.

c. Gọi I là giao điểm của MO với đường tròn (O). Chứng minh I là tâm của đường tròn nội tiếp tam giác MNP