Đề thi tuyển sinh lớp 10 THPT tỉnh Hưng Yên năm học 2012 - 2013 môn Toán - Có đáp án
Nhằm giúp các bạn chuẩn bị thật tốt kiến thức để làm bài thi đạt hiệu quả cao, Vndoc.com xin giới thiệu: Đề thi tuyển sinh lớp 10 THPT tỉnh Hưng Yên năm học 2012 - 2013 môn Toán - Có đáp án.
Đề thi tuyển sinh lớp 10 môn Toán:
SỞ GIÁO DỤC VÀ ĐÀO TẠO | KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN |
Bài 1: (2 điểm)
a. Cho 
. Chứng minh A là một số tự nhiên.
b. Giải hệ phương trình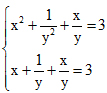 
Bài 2: (2 điểm)
a. Cho Parbol (P): y = x2 và đường thẳng (d): y = (m +2)x – m + 6. Tìm m để đường thẳng (d) cắt Parabol (P) tại hai điểm phân biệt có hoành độ dương.
b. Giải phương trình: 
Bài 3: (2 điểm)
a. Tìm tất cả các số hữu tỷ x sao cho A = x2 + x+ 6 là một số chính phương.
b. Cho x > 1 và y > 1. Chứng minh rằng: 
Bài 4 (3 điểm)
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O, đường cao BE và CF. Tiếp tuyến tại B và C cắt nhau tại S, gọi BC và OS cắt nhau tại M
a. Chứng minh AB. MB = AE.BS
b. Hai tam giác AEM và ABS đồng dạng
c. Gọi AM cắt EF tại N, AS cắt BC tại P. CMR NP vuông góc với BC
Bài 5: (1 điểm)
Trong một giải bóng đá có 12 đội tham dự, thi đấu vòng tròn một lượt (hai đội bất kỳ thi đấu với nhau đúng một trận).
a) Chứng minh rằng sau 4 vòng đấu (mỗi đội thi đấu đúng 4 trận) luôn tìm được ba đội bóng đôi một chưa thi đấu với nhau.
b) Khẳng định trên còn đúng không nếu các đội đã thi đấu 5 trận?
