Định nghĩa hình tam giác cân, tam giác vuông cân

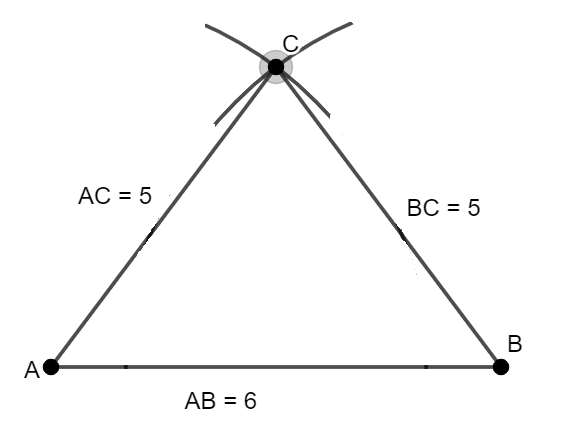
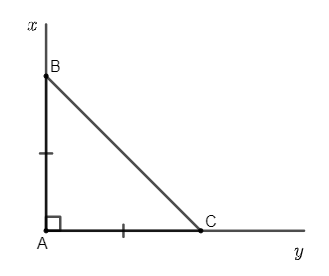
II. Tính chất của tam giác cân

Tính chất 1: Trong một tam giác cân hai góc ở đáy bằng nhau.

Chứng minh:

Giả thiết	Tam giác ABC cân tại A, AB = AC
Kết luận	\(\widehat{ABC}=\widehat{ACB}\)

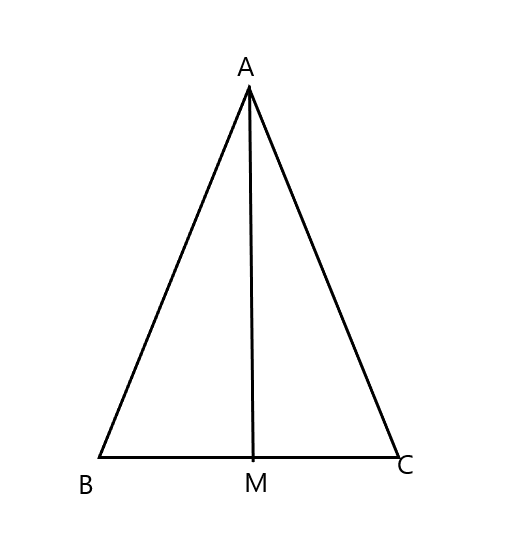
Trong tam giác cân ABC, gọi AM là tia phân giác của góc _{\(\widehat{BAC}\)}

Khi đó ta có \(\widehat{BAM}=\widehat{CAM}\)

Xét tam giác ABM và tam giác ACM có:

AB = AC (gt)

\(\widehat{BAM}=\widehat{CAM}\) (cmt)

AM chung

Suy ta ΔABM = ΔACM (c.g.c) _{\(\Rightarrow \widehat{ABC}=\widehat{ACB}\)} (đpcm)

Tính chất 2: Một tam giác có hai góc bằng nhau thì là tam giác cân.

Giả thiết	Tam giác ABC, \(\widehat{ABC}=\widehat{ACB}\)
Kết luận	Tam giác ABC cân tại A

Trong tam giác ABC, gọi AM là tia phân giác của _{\(\widehat{BAC} \Rightarrow \widehat{BAM} = \widehat{CAM}\)}

Tam giác ABM có \(\widehat{ABM} + \widehat{AMB} + \widehat {BAM} = 180^0\) (tổng 3 góc trong một tam giác)

Tam giác ACM có \(\widehat{ACM}+\widehat{CAM} + \widehat{CMA} = 180^0\) (tổng 3 góc trong một tam giác)

Mà lại có \(\widehat{ABC} = \widehat{ACB}\)

nên \(\widehat{AMB} = \widehat{AMC}\)

Xét tam giác ABM và tam giác ACM có:

\(\widehat{BAM} = \widehat{CAM}\)

\(\widehat{ABC} = \widehat{ACB}\)

\(\widehat{AMB} = \widehat{AMC}\)

Suy ra ΔABM = ΔACM (g - g - g) nên AB  = AC (cạnh tương ứng bằng nhau)

Xét tam giác ABC có AB = AC, suy ra tam giác ABC cân tại A (định nghĩa)

Tính chất 3: Trong một tam giác cân, đường trung trực ứng với cạnh đáy đồng thời là đường phân giác, đường trung tuyến, đường cao của tam giác đó.

Tính chất 4: Trong một tam giác, nếu có một đường trung tuyến đồng thời là đường trung trực thì tam giác là tam giác cân.

Dấu hiệu nhận biết tam giác cân:

Dấu hiệu 1: Nếu một tam giác có hai cạnh bên bằng nhau thì tam giác đó là tam giác cân.

Dấu hiệu 2: Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

III. Công thức tính Diện tích Tam giác cân

- Diễn giải: Diện tích tam giác cân bằng Tích của chiều cao nối từ đỉnh tam giác đó tới cạnh đáy tam giác, sau đó chia cho 2.

- Công thức tính diện tích tam giác cân: S = (a x h)/ 2

+ a: Chiều dài đáy tam giác cân (đáy là một trong 3 cạnh của tam giác)
+ h: Chiều cao của tam giác (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy).

IV. Định nghĩa về tam giác vuông cân

Tam giác vuông cân vừa là tam giác vuông, vừa là tam giác cân hay nói cách khác tam giác vuông là tam giác có 2 cạnh vuông góc và bằng nhau.

Tam giác ABC có AB = AC, AB ⊥ AC thì tam giác ABC vuông cân tại A.