Giải SBT Toán 6 Bài 12: Ước chung và ước chung lớn nhất

Giải sách bài tập Toán lớp 6 Bài 12: Ước chung và ước chung lớn nhất sách Cánh Diều. Các em học sinh có thể tham khảo đối chiếu với bài của mình đã làm. Các lời giải dưới đây bám sát chương trình học cho các em học sinh cùng theo dõi.

>> Bài trước: Giải SBT Toán 6 Bài 11: Phân tích một số ra thừa số nguyên tố

Bài 109 trang 33 SBT Toán 6 tập 1

a) Số nào là ước chung của 15 và 105 trong các số sau: 1; 5; 13; 15; 35; 53?

b) Tìm ƯCLN(27, 156).

c) Tìm ƯCLN(106, 318), từ đó tìm các ước chung của 424, 636.

Đáp án

a) Ta có 15 = 3.5, 105 = 3.5.7

Khi đó Ư CLN(15, 105) = 3.5 = 15

Suy ra ƯC(15, 105) = Ư(15) = {1; 3; 5; 15}.

Vậy trong các số đã cho các số là ước chung của 15 và 105 là: 1; 5; 15.

b) Ta có: 27 = 3³, 156 = 2².3.13.

Khi đó ƯCLN(27, 156) = 3.

Vậy ƯCLN(27, 156) = 3.

c) Ta có: 106 = 2.53, 318 = 2.3.53.

Khi đó ƯCLN(106, 318) = 2.53 = 106.

Ta có: 424 = 106.4, 636 =2.318.

Mà ƯCLN(106, 318) = 2.53 = 106 nên ƯCLN(424, 636) = 2.106 = 212.

Suy ra ƯC(424, 636) = Ư(212) = {1; 2; 4; 53; 106; 212}.

Vậy ƯC(424, 636) = {1; 2; 4; 53; 106; 212}.

Bài 110 trang 33 SBT Toán 6 tập 1

a) Tìm tất cả các ước chung 18, 27, 30, từ đó tìm ước chung lớn nhất của chúng.

b) Tìm ước chung lớn nhất của 51, 102, 144, từ đó tìm ra ước chung của chúng.

Đáp án

a) Ta có: Ư(18) = {1; 2; 3; 6; 9; 18};

Ư(27) = {1; 3; 9; 27};

Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30}.

ƯC(18, 27, 30) = {1; 3}.

Vậy ƯCLN(18, 27, 30) = 3.

b) Ta có: 51 = 3.17, 102 = 2.3.17, 144 = 2⁴.3⁴.

ƯCLN(51, 102, 144) = 3.

Suy ra ƯC(51, 102, 144) = Ư(3) = {1; 3}.

Vậy ƯC(51, 102, 144) = {1; 3}.

Bài 111 trang 33 SBT Toán 6 tập 1

Một lớp học có 27 học sinh nam và 18 học sinh nữ. Có bao nhiêu cách chia lớp đó thành các tổ sao cho số học sinh nam và số học sinh nữ ở mỗi tổ là như nhau? Cách chia nào để mỗi tổ có số học sinh ít nhất?

Đáp án

Vì số học sinh nam và số học sinh nữ ở mỗi tổ là như nhau nên số tổ sẽ là ước chung của 27 và 18.

Ta có: 27 = 3³, 18 = 2.3².

Suy ra ƯCLN(27, 18) = 3² = 9.

ƯC(27, 18) = {1; 3; 9}.

Do đó ta có ba cách chia lớp thành 1 tổ, 3 tổ và 9 tổ, ta có bảng sau:

Để số học sinh trong mỗi tổ là ít nhất thì ta chia lớp đó thành 9 tổ.

Bài 112 trang 34 SBT Toán 6 tập 1

Ba khối 6, 7 và 8 lần lượt có 300 học sinh, 276 học sinh và 252 học sinh xếp thành các hàng dọc để diễu hành sao cho số hàng dọc của mỗi khối là như nhau. Có thể xếp nhiều nhất thành mấy hàng dọc để mỗi khối đều không có ai lẻ hàng? Khi đó ở mỗi hàng dọc của mỗi khối có bao nhiêu học sinh?

Đáp án

Do số hàng dọc của mỗi khối là như nhau nên số hàng dọc sẽ là ước chung của 300, 276, 252.

Hơn nữa cần xếp nhiều nhất thành các hàng dọc để mỗi khối đều không có ai lẻ hàng nên số hàng là ƯCLN(300, 276, 252).

Ta có 300 = 2².3.5², 276 = 2².3.23, 252 = 2².3².7.

ƯCLN(300, 276, 252) = 2².3 = 12.

Vậy có thể xếp nhiều nhất học sinh của ba khối 6, 7 và 8 thành 12 hàng.

Khi đó ở mỗi hàng:

+) Khối 6 có 300:12 = 25 học sinh.

+) Khối 7 có 276:12 = 23 học sinh.

+) Khối 8 có 252:12 = 21 học sinh.

Bài 113 trang 34 SBT Toán 6 tập 1

Tìm số tự nhiên a, biết:

a) 388 chia cho a thì dư 38, còn 508 chia cho a thì dư 18;

b) 1 012 và 1 178 khi chia cho a đều có số dư là 16.

Đáp án

a) Ta có 388 chia cho a nên dư 38 nên 388 – 38 = 350 chia hết cho a (a > 38);

và 508 chia cho a thì dư 18 nên 508 – 18 = 490 chia hết cho a (a > 18).

Suy ra a là ước chung của 350 và 490.

Ta có 350 = 2.5².7, 490 = 2.5.7².

ƯCLN(350; 490) = 2.5.7 = 70.

ƯC(350, 490) = Ư(70) = {1; 2; 5; 7; 10; 14; 35; 70}.

Mà a > 38 nên a = 70.

Vậy a = 70.

b) Ta có 1 012 và 1 178 khi chia cho a đều có số dư là 16 nên 1 012 – 16 = 996, 1 178 – 16 = 1 162 chia hết cho a (a > 16).

Suy ra a là ước chung của 996 và 1 162.

Ta có: 996 = 2².3.83, 1 162 = 2.7.83.

ƯCLN(996, 1 162) = 2.83 = 166.

ƯC(996, 1 162) = Ư(166) = {1; 2; 83; 166}.

Vì a > 16 nên a ∈ {83; 166}.

Vậy a ∈ {83; 166}.

Bài 114 trang 34 SBT Toán 6 tập 1

Tìm số tự nhiên n để hai số sau nguyên tố cùng nhau:

a) n + 2 và n + 3;

b) 2n + 1 và 9n + 4.

Đáp án

a) Đặt d = ƯCLN(n + 2, n + 3).

Suy ra n + 2 chia hết cho d, n + 3 chia hết cho d.

Ta có n + 3 = n + 2 + 1.

Mà n + 2 chia hết cho d nên 1 chia hết cho d. Do đó d = 1.

Vậy n + 2 và n + 3 là hai số nguyên tố cùng nhau với mọi số tự nhiên n.

b) Đặt d = ƯCLN(2n + 1, 9n + 4).

Suy ra 2n + 1, 9n + 4 chia hết cho d. Do đó 9(2n + 1) cũng chia hết cho d

Ta có 9(2n + 1) = 18n + 9 = 2(9n + 4) + 1.

Mà 9n + 4 chia hết cho d nên 1 cũng chia hết cho d. Do đó d = 1.

Vậy 2n + 1, 9n + 4 là hai số nguyên tố cùng nhau với mọi số tự nhiên n.

Bài 115 trang 34 SBT Toán 6 tập 1

Tìm các số tự nhiên a, b, biết:

a) a + b = 192 và ƯCLN(a, b) = 24;

b) ab = 216 và ƯCLN(a, b) = 6.

Đáp án

a) Vì ƯCLN(a, b) = 24 nên a = 24p, b = 24q với p, q là các số tự nhiên và nguyên tố cùng nhau.

Thay a = 24p và b = 24q vào biểu thức a + b = 192 ta được:

24p + 24q = 192

24(p + q) = 192

P + q = 8.

Do p, q là các số tự nhiên và nguyên tố cùng nhau nên ta có các cặp (p; q) tương ứng là: (1; 7), (7; 1), (3; 5), (5; 3).

+) Với p = 1, q = 7 thì a = 24, b = 168;

+) Với p = 7, q = 1 thì a = 168, b = 24;

+) Với p = 3, q = 5 thì a = 72, b =120;

+) Với p = 5, q = 3 thì a = 120, b = 72.

Vậy ta có các cặp (a, b) là: (168; 24), (24; 168), (72; 120), (120; 72).

b) Vì ƯCLN(a, b) = 6 nên a = 6p, b = 6q với p, q là các số tự nhiên và nguyên tố cùng nhau.

Thay a = 6p và b = 6q vào biểu thức ab = 216 ta được:

6p.6q = 216

36pq = 216

pq = 6.

Do p, q là các số tự nhiên và nguyên tố cùng nhau nên ta có các cặp (p; q) tương ứng là: (1; 6), (6; 1), (3; 2), (2; 3).

+) Với p = 1, q = 6 thì a = 6.1 = 6, b = 6.6 = 36;

+) Với p = 6, q = 1 thì a = 6.6 = 36, b = 6.1 = 6;

+) Với p = 3, q = 2 thì a = 6.3 = 18, b = 6.2 = 12;

+) Với p = 2, q = 3 thì a = 6.2 = 12, b = 6.3 = 18.

Vậy ta có các cặp (a, b) là: (6; 36), (36; 6), (18; 12), (18; 12).

Bài 116 trang 34 SBT Toán 6 tập 1

Cho a,b là hai số nguyên tố cùng nhau. Chứng tỏ rằng 5a + 2b và 7a + 3b cũng là hai số nguyên tố cùng nhau.

Đáp án

Gọi d là ƯCLN của 5a + 2b và 7a +3b. Khi đó, 5a+2b chia hết cho d; 7a +3b chia hết cho d

Nên 7.(5a+2b) ; 5.(7a+3b) ; 3.(5a+2b) và 2.(7a+3b) chia hết cho d

Suy ra 7.(5a+2b) – 5.(7a+3b) cũng chia hết cho d

3.(5a+2b) – 2.(7a+3b) cũng chia hết cho d

Ta được b chia hết cho d và a chia hết cho d

Mà a,b là 2 số nguyên tố cùng nhau nên d=1

Vậy 5a+2b và 7a+3b cũng là hai số nguyên tố cùng nhau.

Bài 117 trang 34 SBT Toán 6 tập 1

Rút gọn các phân số sau về phân số tối giản:

a) \(\frac{{12}}{{24}};\frac{{13}}{{39}};\frac{{35}}{{105}}\)

b) \(\frac{{120}}{{245}};\frac{{134}}{{402}};\frac{{213}}{{852}}\)

c) \(\frac{{234}}{{1170}};\frac{{1221}}{{3663}};\frac{{2133}}{{31995}}\)

Đáp án

a) Ta có:

\(\begin{array}{l}\frac{{234}}{{1170}} = \frac{{234:234}}{{1170:234}} = \frac{1}{5};\\\frac{{1221}}{{3663}} = \frac{{1221:1221}}{{3663:1221}} = \frac{1}{3};\\\frac{{2133}}{{31995}} = \frac{{2133:2133}}{{31995:2133}} = \frac{1}{{15}}.\end{array}\)

b) Ta có:

\(\begin{array}{l}\frac{{120}}{{245}} = \frac{{120:5}}{{245:5}} = \frac{{24}}{{49}};\\\frac{{134}}{{402}} = \frac{{134:134}}{{402:134}} = \frac{1}{3};\\\frac{{213}}{{852}} = \frac{{213:213}}{{852:213}} = \frac{1}{3}.\end{array}\)

c) Ta có:

\(\begin{array}{l}\frac{{234}}{{1170}} = \frac{{234:234}}{{1170:234}} = \frac{1}{5};\\\frac{{1221}}{{3663}} = \frac{{1221:1221}}{{3663:1221}} = \frac{1}{3};\\\frac{{2133}}{{31995}} = \frac{{2133:2133}}{{31995:2133}} = \frac{1}{{15}}.\end{array}\)

Bài 118 trang 34 SBT Toán 6 tập 1

Một số học sinh đứng nắm tay nhau xếp thành hình vòng tròn lớn tham gia hoạt động tập thể. Thầy An đi quanh vòng tròn và gắn cho mỗi học sinh một số thứ tự 1,2,3,4,5,…(Hình 4) và nhận thấy học sinh được gắn số 12 đứng đối diện với học sinh được gắn số 30. Thầy tách các học sinh được gắn số từ số 1 đến số 12 vào nhóm 1, từ số 13 đến số cuối cùng trên vòng tròn vào nhóm 2. Thầy muốn chia các học sinh của mỗi nhóm vào các câu lạc bộ(số câu lạc bộ nhiều hơn 1) sao cho số học sinh ở từng nhóm của mỗi câu lạc bộ là như nhau.

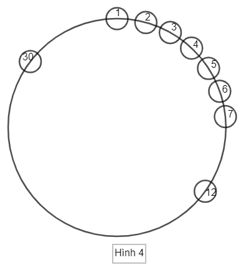
a) Thầy An có bao nhiêu cách để chia học sinh vào các câu lạc bộ?

b) Số câu lạc bộ nhiều nhất mà thầy An có thể chia là bao nhiêu?

Đáp án

Vì học sinh được gắn số 12 đứng đối diện với học sinh được gắn số 30 nên số học sinh đứng trên nửa vòng tròn là 30 – 12 = 18 em. Do đó, số học sinh trên cả vòng tròn là 2. 18 = 36 em

Vì thầy tách các học sinh được gắn số từ số 1 đến số 12 vào nhóm 1, từ số 13 đến số cuối cùng trên vòng tròn vào nhóm 2 nên nhóm 1 có 12 em, nhóm 2 có 24 em

Để số học sinh ở từng nhóm của mỗi câu lạc bộ là như nhau và số câu lạc bộ nhiều hơn 1 thì số câu lạc bộ là ước chung lớn hơn 1 của 12 và 24, tức là có thể là 2;3;4;6;12

a) Vậy thầy An có 5 cách để chia học sinh vào các câu lạc bộ

b) Số câu lạc bộ nhiều nhất mà thầy An có thể chia là ƯCLN(12,24) = 12

>> Bài tiếp theo: Giải SBT Toán 6 Bài 13: Bội chung và bội chung nhỏ nhất

Thông qua lời giải Toán trên các em học sinh có thể luyện tập các dạng Toán trong chuyên mục Toán lớp 6 Cánh Diều phù hợp với nội dung chương trình mình đang học.

Các em học sinh tham khảo thêm Toán lớp 6 Kết nối tri thức và Toán lớp 6 Chân Trời Sáng Tạo. VnDoc liên tục cập nhật lời giải cũng như đáp án sách mới của SGK cũng như SBT các môn cho các bạn cùng tham khảo.