Giải SBT Toán 6 Bài 11: Phân tích một số ra thừa số nguyên tố
Giải sách bài tập Toán lớp 6 Bài 11: Phân tích một số ra thừa số nguyên tố đầy đủ Có đáp án chi tiết. Các em học sinh có thể tham khảo đối chiếu với bài của mình đã làm. Các lời giải dưới đây các em luyện giải bài tập tại nhà mà không cần sách giải.
>> Bài trước: Giải SBT Toán 6 Bài 10: Số nguyên tố. Hợp số
Bài 11 Phân tích một số ra thừa số nguyên tố
- Bài 99 trang 31 SBT Toán 6 tập 1
- Bài 100 trang 31 SBT Toán 6 tập 1
- Bài 101 trang 31 SBT Toán 6 tập 1
- Bài 102 trang 31 SBT Toán 6 tập 1
- Bài 103 trang 31 SBT Toán 6 tập 1
- Bài 104 trang 31 SBT Toán 6 tập 1
- Bài 105 trang 32 SBT Toán 6 tập 1
- Bài 106 trang 32 SBT Toán 6 tập 1
- Bài 107 trang 32 SBT Toán 6 tập 1
- Bài 108 trang 32 SBT Toán 6 tập 1
Bài 99 trang 31 SBT Toán 6 tập 1
Phân tích các số sau ra thừa số nguyên tố: 16; 23; 120; 625.
Đáp án
+) Ta có:
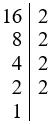
Vậy 16 = 24.
+) Ta có:
![]()
Vậy 23 = 23.
+) Ta có:
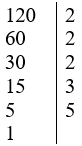
Vậy 120 = 23.3.5.
+) Ta có:
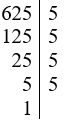
Vậy 625 = 54.
Bài 100 trang 31 SBT Toán 6 tập 1
Thực hiện mỗi phép tính sau, rồi phân tích kết quả ra thừa số nguyên tố:
a) 777:7 + 361:192;
b) 3.52 – 3.17 + 43.7.
Đáp án
a) 777:7 + 361:192
= 777:7 + 361:361
= 111 + 1
= 112.
Ta có:

Vậy 112 = 24.7.
b) 3.52 – 3.17 + 43.7
= 3.25 – 3.17 + 64.7
= 75 – 51 + 448
= 472
Ta có:
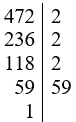
Vậy 472 = 23.59.
Bài 101 trang 31 SBT Toán 6 tập 1
Phân tích 225 và 1 200 ra thừa số nguyên tố rồi cho biết mỗi số đó chia hết cho những số nguyên tố nào.
Đáp án
Ta có:
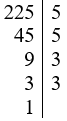
Vậy 225 = 32.52
Suy ra 225 chia hết cho các số nguyên tố là 3 và 5.
Ta có:
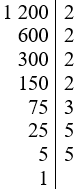
Vậy 1 200 = 24.3.52.
Suy ra 1 200 chia hết cho các số nguyên tố là 2, 3 và 5.
Bài 102 trang 31 SBT Toán 6 tập 1
Bạn Lan khẳng định: “ Khi phân tích số tự nhiên a ra thừa số nguyên tố, nếu a = p.q 2 thì a có tất cả 6 ước”. Theo em, bạn Lan khẳng định đúng hay sai? Vì sao?
Đáp án
Ta có a = p.q 2 nên tập các Ư(a) = {1; p; q; q 2 ; pq; pq 2 }. Do đó a có 6 ước là đúng.
Bài 103 trang 31 SBT Toán 6 tập 1
Cho a = 7 2 .11 3 . Trong các số 7a, 11a, 13a, số nào có nhiều ước nhất?
Đáp án
Ta có: 7a = 7. 72.113 = 73.113.
Suy ra 7a có tất cả (3 + 1).(3 + 1) = 4.4 = 16 ước.
Ta có: 11a = 11.72.113 = 72.114.
Suy ra 11a có tất cả (2 + 1).(4 + 1) = 3.5 = 15 ước.
Ta có: 13a = 13.72.113.
Suy ra 13a có tất cả (2 + 1).(3 + 1).(1 + 1) = 3.4.2 = 24 ước.
Vậy số 13a là số nhiều ước nhất.
Bài 104 trang 31 SBT Toán 6 tập 1
Tìm số tự nhiên n, biết:
a) 2 + 4 + 6 + … + 2.(n – 1) + 2n = 210.
b) 1 + 3 + 5 + … + (2n – 3) + (2n – 1) = 225.
Đáp án
a) Số số hạng của VT là: (2n – 2):2 + 1 = n – 1 + 1 = n số.
Khi đó: 2 + 4 + 6 + … + 2.(n – 1) + 2n = (2n + 2).n:2 = n.(n+1).
Theo đầu bài, ta có: n(n + 1) = 210
Ta có:
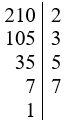
Suy ra 210 = 2.3.4.5= 14.15.
Vậy n = 14.
b) Số số hạng của VT là: (2n – 1 – 1):2 + 1 = (2n – 2):2 + 1 = n – 1 + 1 = n.
Khi đó 1 + 3 + 5 + … + (2n – 3) + (2n – 1) = (2n – 1 + 1).n:2 = 2n.n:2 = n2.
Ta có 223 = 32.52 = 152.
Vậy n = 15.
Bài 105 trang 32 SBT Toán 6 tập 1
Bạn Khanh có 16 cái bút. Bạn Khanh muốn chia số bút đó vào các hộp sao cho số bút của các hộp bằng nhau và mỗi hộp ít nhất hai cái. Bạn Khanh có thể xếp 16 cái bút đó vào mấy hộp? (Kể cả trường hợp xếp vào một hộp).
Đáp án
Vì để xếp 16 cái bút vào các hộp sao cho số bút của các hộp bằng nhau nên số hộp bút là ước của 16.
Ta có: 16 = 24 nên các ước của 16 là: 1; 2; 4; 8; 16.
Ta có bảng sau:
|
Số hộp bút |
Số bút trong mỗi hộp |
|
1 |
16 |
|
2 |
8 |
|
4 |
4 |
|
8 |
2 |
|
16 |
1 |
Vì mỗi hộp có ít nhất hai cái bút nên ta loại trường hợp chia thành 16 hộp bút.
Vậy bạn Khanh có thể xếp số bút đó vào 1 hộp, 2 hộp, 4 hộp hoặc 8 hộp.
Bài 106 trang 32 SBT Toán 6 tập 1
Một trường có 1 015 học sinh, cần phải xếp mỗi hàng bao nhiêu học sinh để số học sinh trong mỗi hàng là như nhau? Biết rằng số hàng không quá 40 hàng và không ít hơn 10 hàng.
Đáp án
Xếp 1 015 học sinh thành các hàng sao cho số học sinh mỗi hàng là như nhau nên số hàng là ước của 1 015.
Ta có: 1 015 = 5.7.29.
Ta có bảng sau:
|
Số hàng |
Số học sinh mỗi hàng |
|
1 |
1 015 |
|
5 |
203 |
|
7 |
145 |
|
29 |
35 |
|
35 |
29 |
|
145 |
7 |
|
203 |
5 |
|
1 015 |
1 |
Vì số hàng không quá 40 hàng và không ít hơn 10 hàng nên ta có thể xếp 1 015 thành 29 hàng hoặc 35 hàng.
Bài 107 trang 32 SBT Toán 6 tập 1
Học sinh lớp 6A nhận được phần thưởng từ Liên đội nhà trường, mỗi học sinh đều được nhận số phần thưởng như nhau. Cô tổng phụ trách đã phát hết 215 quyển vở và 129 quyển truyện cho học sinh lớp 6A. Số học sinh của lớp 6A là bao nhiêu, biết rằng số học sinh của lớp nhiều hơn 10 học sinh?
Đáp án
Vì mỗi học sinh đều nhận được phần thưởng là như nhau nên số học sinh vừa là ước của 215 vừa là ước của 129.
Ta có: 215 = 5.43; 129 = 3.43.
Do đó 43 vừa là ước của 215 vừa là ước của 129 và thỏa mãn lớn hơn 10 nên số học sinh của lớp 6A là 43 học sinh.
Bài 108 trang 32 SBT Toán 6 tập 1
Tìm số tự nhiên n sao cho:
a) 3n + 13 chia hết cho n + 1;
b) 5n + 19 chia hết cho 2n + 1.
Đáp án
a) Ta có: 3n + 13 = 3n + 3 + 10 = 3.(n + 1) + 10.
Vì 3.(n + 1) chia hết cho n + 1 nên để 3n + 13 chia hết cho n + 1 thì 10 phải chia hết cho n + 1 hay n + 1 là ước của 10.
Ta có: 10 = 2.5 nên các ước của 10 là: Ư(10) = {1; 2; 5; 10}.
Ta có bảng sau:
|
n + 1 |
1 |
2 |
5 |
10 |
|
n |
0 |
1 |
4 |
9 |
Vậy n ∈ {0; 1; 4; 9}.
b) 5n + 19 chia hết cho 2n + 1.
Vì 5n + 19 chia hết cho 2n + 1 nên 2(5n + 19) chia hết cho 2n + 1
Xét 2(5n + 19) = 10n + 38 = 10n + 5 + 33 = 5(2n + 1) + 33.
Vì 5.(2n + 1) chia hết cho 2n + 1 nên để 2(5n + 19) chia hết cho 2n + 1 thì 33 phải chia hết cho 2n + 1 hay 2n + 1 thuộc ước của 33.
Ta có bảng sau:
|
2n + 1 |
1 |
3 |
11 |
33 |
|
n |
0 |
1 |
5 |
16 |
Vậy n ∈ {0; 1; 5; 16}.
>> Bài tiếp theo: Giải SBT Toán 6 Bài 12: Ước chung và ước chung lớn nhất
Thông qua lời giải Toán trên các em học sinh có thể luyện tập các dạng Toán trong chuyên mục Toán lớp 6 Cánh Diều phù hợp với nội dung chương trình mình đang học.
Các em học sinh tham khảo thêm Toán lớp 6 Kết nối tri thức và Toán lớp 6 Chân Trời Sáng Tạo. VnDoc liên tục cập nhật lời giải cũng như đáp án sách mới của SGK cũng như SBT các môn cho các bạn cùng tham khảo.



