Giải SBT Toán 6 Bài 9: Dấu hiệu chia hết cho 3, cho 9

Giải sách bài tập Toán lớp 6 Bài 9: Dấu hiệu chia hết cho 3, cho 9. Các em học sinh có thể tham khảo đối chiếu với bài của mình đã làm. Các lời giải dưới đây các em luyện giải bài tập tại nhà mà không cần sách giải.

>> Bài trước: Giải SBT Toán 6 Bài 8: Dấu hiệu chia hết cho 2, cho 5

Bài 77 trang 27 SBT Toán 6 tập 1

Cho các số 27, 45, 881, 916, 2 100, 2 439, 13 118, 35 550, 5 223 411. Trong các số đó:

a) Số nào chia hết cho 3?

b) Số nào lớn hơn 2 000 không chia hết cho 3?

c) Số nào chia hết cho 9?

d) Số nào nhỏ hơn 3 000 không chia hết cho 9?

Đáp án

a) Các số chia hết cho 3 là: 27, 45, 2 100, 2 439, 35 550, 5 223 411 vì các số này đều có tổng các chữ số chia hết cho 3

b) Các số lớn hơn 2 000 là 2 100; 2 439; 13 118; 35 550; 5 223 411. Trong các số này, có số 13 118 không chia hết cho 3 ( do tổng các chữ số của 13 118 là 1+3+1+1+8 = 16 không chia hết cho 3)

Vậy số lớn hơn 2 000 không chia hết cho 3 là 13 118

c) Các số chia hết cho 9 là: 27, 45, 2 439, 35 550, 5 223 411 vì các số này đều có tổng các chữ số chia hết cho 9.

d) Các số nhỏ hơn 3 000 là 27; 45; 881; 916; 2 100; 2 439. Trong các số này, có số 881; 916; 2 100 không chia hết cho 9(do tổng các chữ số của mỗi số này không chia hết cho 9)

Bài 78 trang 27 SBT Toán 6 tập 1

Tìm chữ số x để số \(\overline {x1269}\) thỏa mãn mỗi điều kiện sau:

a) Chia hết cho 3

b) Chia hết cho 9;

c) Chia hết cho 3 nhưng không chia hết cho 9.

Đáp án

Tồng các chữ số của số \(\overline {x1269}\) là : x + 1+2+6+9 = x+18.

a) Để số \(\overline {x1269}\) chia hết cho 3 thì x + 18 chia hết cho 3. Mà 18 chia hết cho 3 nên x cũng phải chia hết cho 3.

Vậy x \(\in\) {3;6;9}

b) Để số \(\overline {x1269}\) chia hết cho 9 thì x + 18 chia hết cho 9. Mà 18 chia hết cho 9 nên x cũng phải chia hết cho 9.

Vậy x = 9

c) Để số \(\overline {x1269}\) chia hết cho 3 nhưng không chia hết cho 9 thì x  \(\in\) {3;6;9} và x\(\ne\) 9. Như vậy x \in {3;6}.

Bài 79 trang 27 SBT Toán 6 tập 1

Có bao nhiêu số có dạng \(\overline {11a10b}\) chia cho 5 dư 1 và chia hết cho 9?

Đáp án

Ta có: \(\overline {11a10b}\) chia cho 5 dư 1 nên b = 1 hoặc b = 6.

+ Nếu b = 1 thì\(\overline {11a10b}\) có tổng các chữ số là 1+1+a+1+0+1= 4+a. Để \(\overline {11a10b}\) chia hết cho 9 thì 4+a chia hết cho 9. Điều này xảy ra khi a = 5

+ Nếu b = 6 thì \(\overline {11a10b}\) có tổng các chữ số là 1+1+a+1+0+6= 9+a. Để \(\overline {11a10b}\) chia hết cho 9 thì 9+a chia hết cho 9. Điều này xảy ra khi a = 0 hoặc a= 9

Vậy có 3 số có dạng \(\overline {11a10b}\) chia cho 5 dư 1 và chia hết cho 9, đó là:

115101; 110106; 119106.

Bài 80 trang 27 SBT Toán 6 tập 1

Không tính giá trị biểu thức, hãy giải thích tại sao mỗi biểu thức sau chia hết cho 3?

a) A= 1 233 + 42 312 + 72 036.

b) B= 111+222+333+…+ 999.

Đáp án

a) Ta có các số 1 233 , 42 312 , 72 036 đều là các số chia hết cho 3 (tổng các chữ số của mỗi số chia hết cho 3) nên tổng A = 1 233 + 42 312 + 72 036 chia hết cho 3)

b) Ta có các số 111; 222; 333; …; 999 đều là các số chia hết cho 3 (tổng các chữ số của mỗi số chia hết cho 3) nên tổng B = 111+222+333+…+ 999 chia hết cho 3)

Bài 81 trang 27 SBT Toán 6 tập 1

Không tính giá trị biểu thức, hãy giải thích tại sao mỗi biểu thức sau chia hết cho 9?

a) P = 81 + 108 + 918

b) M = 12. 585 + 13.63.333+14. 378 225 + 18. 5 142 312;

c) N = 11+22+33+…+99 + 2 021. 60 021.

Đáp án

a) Vì các số 81; 108; 918 đều chia hết cho 9 nên tổng P = 81 + 108 + 918 chia hết cho 9

b) Vì 585; 63; 378 225; 18 chia hết cho 9 nên 12. 585 ; 13.63.333; 14. 378 225 ; 18. 5 142 312 chia hết cho 9. Vậy tổng M = 12. 585 + 13.63.333+14. 378 225 + 18. 5 142 312 chia hết cho 9.

c) Ta có: 11+22+33+…+99 = (11+88)+(22+77)+(33+66)+(44+55)+99 = 99+99+99+99+99 =5. 99

Vì 99 chia hết cho 9 nên 5.99 chia hết cho 9. Do đó 11+22+33+…+99 chia hết cho 9. Mà 60 021 chia hết cho 9 nên 2 021. 60 021 chia hết cho 9

Vậy N = 11+22+33+…+99 + 2 021. 60 021 chia hết cho 9

Bài 82 trang 27 SBT Toán 6 tập 1

Tìm các số tự nhiên a,b sao cho:

a) \(\overline {a26b}\) chia hết cho cả 2,3,5 và 9;

b) 123. a + 9 873.b = 2 227 691.

Đáp án

a) Số \(\overline {a26b}\) chia hết cho cả 2 và 5 nên b = 0

Ta có số \(\overline {a26b}\) có tổng các chữ số là a+2+6+0 = a+8. Để \(\overline {a26b}\) chia hết cho 3 và 9 thì a+8 chia hết cho 9 hay a =1

Vậy a=1; b= 0

b) Ta có 123 và 9 873 chia hết cho 3 nên 123. a + 9 873.b cũng phải chia hết cho 3. Nhưng 2 227 691 không chia hết cho 3. Như vậy, không tìm được số tự nhiên a,b nào thỏa mãn

Bài 83 trang 27 SBT Toán 6 tập 1

a) Có bao nhiêu số tự nhiên có hai chữ số chia cho 3 dư 1?

b) Có bao nhiêu số tự nhiên có ba chữ số chia cho 9 dư 2?

c) Có bao nhiêu số tự nhiên có hai chữ số \(\overline {ab}\) sao cho\(\overline {ab} + \overline {ba}\) chia hết cho 9?

Đáp án

a) Các số tự nhiên có hai chữ số chia cho 3 dư 1 là: 10; 13;…; 94; 97.

Số các số tự nhiên có hai chữ số chia cho 3 dư 1 là:

(97 – 10 ) : 3 +1 = 30 (số)

b) Các số tự nhiên có hai chữ số chia cho 9 dư 2 là: 101; 110; …; 983; 992.

Số các số tự nhiên có hai chữ số chia cho 9 dư 2 là:

(992 – 101) : 9 +1 = 100 (số)

c) Ta có: \(\overline {ab} + \overline {ba}\) = a.10+b+b.10+a=11.a +11.b=11.(a+b)

Để \(\overline {ab} + \overline {ba}\) chia hết cho 9 thì a+b phải chia hết cho 9 hay\(\overline {ab}\) chia hết cho 9.

Các số \(\overline {ab}\) thỏa mãn là 18;27;…;99. Chú ý điều kiện b \(\ne\) 0 . Vậy có 9 số tự nhiên thảo mãn điều kiện

Bài 84 trang 28 SBT Toán 6 tập 1

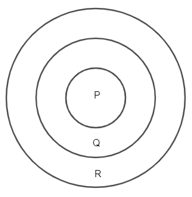
Bạn Minh chơi trò phi tiêu với ba cái tiêu. Lần thứ nhấ, bạn Minh phi 2 tiêu vào vùng Q và 1 tiêu vào vùng R thì được 12 điểm. Lần thứ 2, bạn Minh phi 2 tiêu vào vùng P và 1 tiêu vào vùng R thì được 18 điểm. Lần thứ ba, bạn Minh phi trúng mỗi vùng 1 tiêu. Hỏi số điểm lần thứ ba của bạn Minh có chia hết cho cả 3 và 5 không? Tại sao?

Đáp án

Tổng tổng số điểm Minh phi ở 2 lần đầu là:

12 + 18=30 (điểm)

Trong tổng cả 2 lần đầu, Minh phi vào mỗi vùng 2 lần. Do đó, khi phi vào mỗi vùng 1 lần, thì Minh được số điểm là:

30 : 2 =15 (điểm)

Vậy lần 3 bạn Minh phi được 15 điểm. 15 chia hết cho cả 3 và 5 nên số điểm lần thứ ba của bạn Minh chia hết cho cả 3 và 5

Bài 85 trang 28 SBT Toán 6 tập 1

Cho a là số tự nhiên có 2 004 chữ số và chia hết cho 9. Gọi b là tổng các chữ số của a; c là tổng các chữ số của b và d là tổng các chữ số của c. Tính d.

Đáp án

Vì a chia hết cho 9 nên tổng các chữ số của a chia hết cho 9 hay b chia hết cho 9. Do c là tổng các chữ số của b và d là tổng các chữ số của c nên c, d cũng chia hết cho 9

Vì a là số tự nhiên có 2 004 chữ số, mỗi chữ số lại không lớn hơn 9 nên b không lớn hơn

2 004.9 = 18 036. Do đó, b không có lớn hơn 5 chữ số và c không lớn hơn 5.9 = 45. Mà c khác 0 và c chia hết cho 9 nên c ∈ {9;18; 27; 36}

Như vậy d = 9

Bài 86 trang 28 SBT Toán 6 tập 1

Viết liên tiếp các số tự nhiên từ 10 đến 99 liền nhau ta được một số tự nhiên. Hỏi số đó chia hết cho 9 hay không? Vì sao?

Đáp án

Gọi A là số được viết bởi 90 số từ 10 đến 99.

Tổng các chữ số hàng đơn vị của số này là: (0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9). 9 = 405.

Tổng các chữ số hàng chục của số này là: (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9).10 = 450.

Vậy tổng các chữ số của số A là: 405 + 450 = 855.

Vì 8 + 5 + 5 =18 chia hết cho 9 nên 855 chia hết cho 9.

Vậy số A chia hết cho 9.

Bài 87 trang 28 SBT Toán 6 tập 1

Không thực hiện phép tính, hãy giải thích tại sao phép nhân là sai: 7 654.658 = 5 136 332.

Đáp án

Ta có: 7 + 6 + 5 + 4 = 22 chia cho 9 dư 4 nên 7 654 chia cho 9 dư 4.

Ta lại có: 6 + 5 + 8 = 19 chia cho 9 dư 1 nên 658 chia cho 9 dư 1.

Do đó 7 654.658 chia 9 dư 4.

Ta có: 5 + 1 + 3 + 6 + 3 + 3 + 2 = 23 chia cho 9 dư 3 nên 5 136 332 chia cho 9 dư 3.

Vậy phép tính 7 654.658 = 5 136 332 là sai.

Bài 88 trang 28 SBT Toán 6 tập 1

Một công ty có 9 contenơ hàng với khối lượng hàng mỗi contenơ là: 193 tạ, 239 tạ, 277 tạ, 297 tạ, 316 tạ, 321 tạ, 329 tạ, 346 tạ, 355 tạ. Trong sáu tháng đầu năm công ty đó đã xuất khẩu 8 contenơ hàng, trong đó lượng hàng xuất khẩu của Quý II gấp 8 lần Quý I. Contenơ hàng còn lại có khối lượng bằng bao nhiêu?

Đáp án

Tổng khối lượng hàng của 9 contenơ hàng là:

193 + 239 + 277 + 297 + 316 + 321 + 329 + 346 + 355 = 2 673 (tạ).

Ta có: 2 + 6 + 7 + 3 = 18 chia hết cho 9 nên 2 673 chia hết cho 9.

Vì lượng hàng xuất khẩu của Quý II gấp 8 lần Quý I nên số lượng hàng trong 6 tháng đầu năm phải chia hết cho 9.

Do đó khối lượng hàng của contenơ còn lại phải chia hết cho 9.

Trong số 9 contenơ trên chỉ có contenơ có khối lượng 297 tạ là thỏa mãn chia hết cho 9.

Vậy contenơ hàng còn lại có khối lượng là 297 tạ.

>> Bài tiếp theo: Giải SBT Toán 6 Bài 10: Số nguyên tố. Hợp số

Thông qua lời giải Toán trên các em học sinh có thể luyện tập các dạng Toán trong chuyên mục Toán lớp 6 Cánh Diều phù hợp với nội dung chương trình mình đang học.

Các em học sinh tham khảo thêm Toán lớp 6 Kết nối tri thức và Toán lớp 6 Chân Trời Sáng Tạo. VnDoc liên tục cập nhật lời giải cũng như đáp án sách mới của SGK cũng như SBT các môn cho các bạn cùng tham khảo.