Tổng hợp đề thi thử học sinh giỏi Lớp 12 môn Toán năm 2013

ĐỀ SỐ 1
(Thời gian: 180 phút)

Câu I: (4 điểm)

Cho hàm số y = x³ + 3x² - 2 (C)

1/ Khảo sát và vẽ đồ thị.

2/ Giải bất phương trình : 0 ≤ 2006 + 6018x² - 4012 ≤ 4012.

3/ Viết phương trình tiếp tuyến của đồ thị (C). Biết tiếp tuyến đi qua A(0; -2)

Câu II: (2 điểm)

Tính

Câu III: (2 điểm)

Giải và biện luận phương trình theo tham số m: |x + 1| + |x - 1| = m

Câu IV: (4 điểm)

Giải các phương trình sau:

1/ Sin(π/2 - πcosx)= cos(3πcosx)

2/ 6^x + 4^x = 2.9^x

Câu V: (2 điểm)

Chứng minh điều kiện cần và đủ để tam giác ABC vuông: Cos²A + Cos²B + Cos²C = 1

Câu VI: (2 điểm): Tính giới hạn sau:

Câu VII: (2 điểm):

Trong hệ Oxy cho hai đường thẳng d₁//d₂ lần lượt có phương trình là: d₁: x - y + 2 = 0; d₂: x - y - 2 = 0

1/ Viết phương trình đường thẳng d₃ đi qua điểm A(-2; 0) và vuông góc với d₂

2/ Viết phương trình đường thẳng d₄ sao cho d₁, d₂, d₃, d₄ cắt nhau tạo thành một hình vuông.

Câu XIII: (2 điểm)

Chứng minh rằng với a,b> 0 ta có: a⁵ + b⁵ ≥ a⁴b + ab⁴

ĐỀ SỐ 2
(Thời gian: 180 phút)

Câu 1. (3 điểm)

1. Khảo sát và vẽ đồ thị của hàm số: y = |x|³ - 3|x| - 2 (ξ)

2. Gọi d là đường thẳng đi qua M(2;0) và có hệ số góc k. Tìm k để đường thẳng d cắt (ξ) tại 4 điểm phân biệt.

Câu 2. (4 điểm)

1. Cho dãy số (x_n) xác định bởi: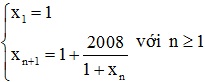

Chứng minh rằng (x_n) có giới hạn và tìm giới hạn đó.

2. Tìm m để phương trình: có nghiệm.

Câu 3. (2 điểm)

Cho 1/4 < a, b, c, d < 1. Tìm giá trị nhỏ nhất của biểu thức:

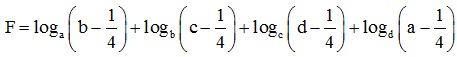
Câu 4. (3 điểm)

1. Giải phương trình:

2. Tìm nghiệm của phương trình thỏa mãn: 2008 < x < 2009

Câu 5. (2 điểm)

Cho tam giác ABC biết A(1; -2), hai đường phân giác trong của góc B và C lần lượt có phương trình là: (d₁): 3x + y - 3 = 0 và (d₂): x - y - 1 = 0. Lập phương trình các cạnh của tam giác ABC.

Câu 6. (4 điểm)

Cho một tam diện vuông Oxyz và một điểm A cố định bên trong tam diện. Gọi khoảng cách từ A đến ba mặt phẳng Oyz, Ozx, Oxy lần lượt là a, b, c. Một mặt phẳng (α) qua A cắt Ox, Oy, Oz lần lượt tại M, N, P.

1. Chứng minh rằng:

2. Xác định vị trí của mặt phẳng (α) để thể tích của tứ diện OMNP đạt giá trị nhỏ nhất. Khi thể tích tứ diện OMNP nhỏ nhất, hãy chỉ rõ vị trí điểm A.

3. Chứng minh rằng: (MN + NP + PM)² ≤ 6(OM² + ON² + OP²)

Câu 7. (2 điểm)

Cho 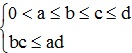. Chứng minh rằng: a^b.b^c.c^d.d^a ≥ a^d.d^c.c^b.b^a