Công thức hệ thức lượng trong tam giác Toán 10 đầy đủ và dễ hiểu nhất

Công thức hệ thức lượng trong tam giác Toán 10 là nội dung trọng tâm giúp học sinh nắm vững mối quan hệ giữa các cạnh và góc trong tam giác. Bài viết tổng hợp đầy đủ, chi tiết và dễ hiểu nhất các hệ thức lượng trong tam giác vuông, tam giác thường, kèm ví dụ minh họa và phương pháp ghi nhớ nhanh. Đây là tài liệu hữu ích giúp học sinh học tốt hình học Toán 10 và chuẩn bị cho các kỳ kiểm tra, thi học kỳ, ôn thi THPT Quốc gia.

I. Công thức hệ thức lượng trong tam giác vuông

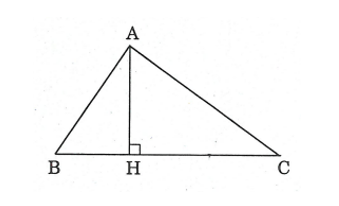
Cho tam giác \(ABC\) vuông tại \(A,\) \(AH\) là đường cao. Ta có các hệ thức sau:

\(BC^{2} + AB^{2} + AC^{2}\) (định lý Pythagore) \(AB^{2} = BH.BC\) \(AC^{2} = CH.BC\) \(AH^{2} = HB.HC\) \(AH.BC = AB.AC\) \(\frac{1}{AH^{2}} = \frac{1}{AB^{2}} + \frac{1}{AC^{2}}\) \(AC = BC.sinB\);       \(AB = BC.sinC\)\(AC = BC.cosC\);     \(AB = BC.cosB\) \(AB = AC.tanC = AC.cotB\) \(AC = AB.tanB = AB.cotC\)

Hình vẽ minh họa:

II. Công thức hệ thức lượng trong tam giác

1. Định lí côsin

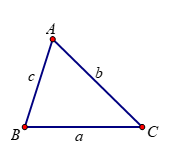
Trong tam giác \(ABC\) với \(BC = a,\ \ AC = b\) và \(AB = c\). Ta có:

\(a^{2} = b^{2} + c^{2} - 2bc.cosA\) \(b^{2} = c^{2} + a^{2} - 2ca.cosB\) \(c^{2} = a^{2} + b^{2} - 2ab.cosC\) \(c^{2} = a^{2} + b^{2} - 2ab.cosC\) Hệ quả: \(\cos A = \frac{b^{2} + c^{2} - a^{2}}{2bc}\) \(\cos B = \frac{c^{2} + a^{2} - b^{2}}{2ca}\) \(\cos C = \frac{a^{2} + b^{2} - c^{2}}{2ab}\)

Hình vẽ minh họa:

b) Định lí sin

Trong tam giác \(ABC\) với \(BC = a,\ \ AC = b\), \(AB = c\) và R là bán kính đường tròn ngoại tiếp. Ta có:

\(\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R\)

c) Công thức tính diện tích tam giác

Với tam giác \(ABC\) ta kí hiệu \(h_{a},\ \ h_{b},\ \ h_{c}\) là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, AB; R, r lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp tam giác; \(p = \frac{a + b + c}{2}\) là nửa chu vi tam giác; S là diện tích tam giác.

Công thức tính độ dài đường cao

\(h_{a} = \frac{2S}{a},\ \ \ h_{b} = \frac{2S}{b},\ \ \ h_{c} = \frac{2S}{c}.\)

Công thức tính bán kính đường tròn ngoại tiếp tam giác

Biết độ dài cạnh và góc đối diện thì dùng định lí sin

\(\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R\)

\(\Rightarrow R = \frac{a}{2sinA} = \frac{b}{2sinB} = \frac{c}{2sinC}.\)

Ngoài ra \(S = \frac{abc}{4R} \Rightarrow R = \frac{abc}{4S}\)

Công thức tính bán kính đường tròn nội tiếp

\(S = pr \Rightarrow r = \frac{S}{p} = \frac{2S}{a + b + c}\)

\(r = (p - a)tan\frac{A}{2} = (p - b)tan\frac{B}{2} = (p - c)tan\frac{C}{2}\)

Công thức tính kính đường tròn bàng tiếp

\(r_{a} = p\tan\frac{A}{2}\)       \(r_{B} = p\tan\frac{B}{2}\)           \(r_{c} = p\tan\frac{C}{2}\)

III. Giá trị lượng giác của một góc từ 0⁰ đến 180⁰

1. Định nghĩa

Trong mặt phẳng tọa độ \(Oxy\). Với mỗi góc\(\alpha\left( 0^{0} \leq \alpha \leq 180^{0} \right)\), ta xác định điểm M trên trên đường nửa đường tròn đơn vị tâm O sao cho \(\alpha = \widehat{xOM}\). Giả sử điểm M có tọa độ \((x;y)\).

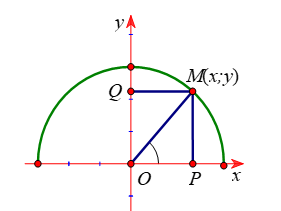
Khi đó:

\(\sin\alpha = y;cos\alpha = x;tan\alpha = \frac{y}{x}(\alpha \neq 90^{0})\)

\(\cot\alpha = \ \ \frac{x}{y}\ (\alpha \neq 0^{0},\alpha \neq 180^{0})\)

Các số \(\sin\alpha,\ \cos\alpha,\ \tan\alpha,\ \cot\beta\) được gọi là giá trị lượng giác của góc \(\alpha\).

Chú ý: Từ định nghĩa ta có:

Gọi P, Q lần lượt là hình chiếu của M lên trục Ox, Oy khi đó \(M\left( \overline{OP};\overline{OQ} \right)\).

Với \(0^{0} \leq \alpha \leq 180^{0}\) ta có \(0 \leq \sin\alpha \leq 1;\ \ - 1 \leq \cos\alpha \leq 1\)

Dấu của giá trị lượng giác

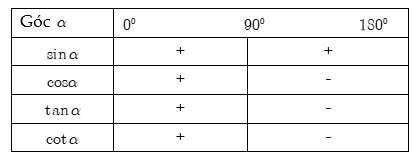
2. Tính chất

Góc phụ nhau	Góc bù nhau
\(\sin(90^{0} - \alpha) =\cos\alpha\) \(\cos(90^{0} - \alpha) =\sin\alpha\) \(\tan(90^{0} - \alpha) =\cot\alpha\) \(\cot(90^{0} - \alpha) =\tan\alpha\)	\(\sin(180^{0} - \alpha) =\sin\alpha\) \(\cos(180^{0} - \alpha) = -\cos\alpha\) \(\tan(180^{0} - \alpha) = -\tan\alpha\) \(\cot(180^{0} - \alpha) = -\cot\alpha\)

3. Giá trị lượng giác của các góc đặc biệt

4. Các hệ thức lượng giác cơ bản

1) \(\tan\alpha = \frac{\sin\alpha}{\cos\alpha}(\alpha \neq 90^{0})\)                              2) \(\cot\alpha = \frac{\cos\alpha}{\sin\alpha}(\alpha \neq 0^{0};180^{0})\)

3) \(\tan\alpha.cot\alpha = 1(\alpha \neq 0^{0};90^{0};180^{0})\)              4) \(sin^{2}\alpha + cos^{2}\alpha = 1\)

5) \(1 + tan^{2}\alpha = \frac{1}{cos^{2}\alpha}(\alpha \neq 90^{0})\)                     6) \(1 + cot^{2}\alpha = \frac{1}{sin^{2}\alpha}(\alpha \neq 0^{0};180^{0})\)

-------------------------------------------------------------------

Hy vọng bài viết Công thức hệ thức lượng trong tam giác Toán 10 đầy đủ và dễ hiểu nhất sẽ giúp các em nắm chắc kiến thức trọng tâm và vận dụng tốt trong giải bài tập. Hãy lưu lại tài liệu này để ôn tập hiệu quả, và đừng quên tham khảo thêm các công thức Toán 10 khác để học tốt hơn mỗi ngày!