Đề thi giải toán trên Máy tính cầm tay tỉnh Vĩnh Phúc năm 2009 - 2010 môn Toán THPT (Bổ túc)

SỞ GIÁO DỤC & ĐÀO TẠO VĨNH PHÚC

KỲ THI GIẢI TOÁN TRÊN MTCT BẬC TRUNG HỌC NĂM HỌC 2009 - 2010 ĐỀ THI MÔN: TOÁN - BTTHPT Thời gian làm bài: 150 phút (không kể thời gian giao đề)

Bài 1:

Cho đa thức f(x) biến x là số thực và thoả mãn hệ thức f(x² + 1) = x⁴ + 5x² + 3. Tính gần đúng giá trị của: f(2008, 2009).

Bài 2:

Cho bất phương trình |x| + |y| ≤ n, n thuộc N*. Gọi S_n là số nghiệm nguyên của bất phương trình.

a, Thiết lập công thức tính S_n qua n và S_{n - 1}.

b, Tính S₂₀₀₈.

Bài 3:

Tính gần đúng các giá trị của m và n để đường thẳng y = mx + n đi qua điểm A(151; 253) và tiếp xúc với parabol y = 25x² – 49x + 7/3.

Bài 4:

Biết rằng hàm số y = x⁴ – 2(m - 2008)x² + (2008 - m)⁴ + 2m – 4016 có cực đại, cực tiểu, đồng thời các điểm cực trị của đồ thị hàm số tạo thành một tam giác đều. Tính gần đúng giá trị của m.

Bài 5:

Tính gần đúng các nghiệm của hệ: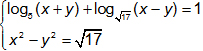

Bài 6:

Cho hình chóp tứ giác đều S.ABCD có AB = 4,56 cm; góc ASC = 79⁰.

a, Tính gần đúng diện tích toàn phần của hình chóp S.ABCD.

b, Tính gần đúng bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.

Bài 7:

Khi sản xuất vỏ hộp sữa bột hình trụ, người ta luôn đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ là ít nhất, tức là diện tích toàn phần của hình trụ là nhỏ nhất. Hãy tính gần đúng diện tích toàn phần của một vỏ hộp sữa bột được làm theo nguyên tắc như trên khi ta muốn thể tích của hộp là 889cm³.

Bài 8:

Cho Elip có phương trình . Gọi R₁, R₂, R₃, R₄ theo thứ tự là diện tích các phần của Elip thuộc góc phần tư thứ I, thứ II, thứ III và thứ IV. Hãy tính: R₁ - R₂ + R₃ - R₄

Bài 9:

Dãy Fibonaci (a_n) là dãy số có a₁ = a2 =1; a_n = a_n-1 + a_n-2 với 2 < n thuộc R. Cho biểu thức: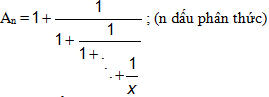

a, Hãy biểu thị A_n với n > 4 theo x và các số hạng của dãy Fibonacci.

b, Tìm x thoả mãn A₂₀₀₈ = x

Bài 10:

Theo dự báo với mức tiêu thụ dầu không đổi như hiện nay thì trữ lượng dầu của một nước sẽ hết sau 50 năm nữa. Nhưng do nhu cầu thực tế, mức tiêu thụ tăng lên 5% mỗi năm. Hỏi sau bao nhiêu năm số dầu dự trữ sẽ hết.