VnDoc.com

Đề thi giữa học kì 1 môn Toán lớp 12, trường THPT Tây Hồ, Hà Nội, năm học 2017 - 2018

Đề thi giữa học kì 1 môn Toán lớp 12

Đề thi giữa học kì 1 môn Toán lớp 12

VnDoc.com xin giới thiệu tới bạn đọc bộ tài liệu: Đề thi giữa học kì 1 môn Toán lớp 12, trường THPT Tây Hồ, Hà Nội, năm học 2017 - 2018, tài liệu gồm 33 câu hỏi trắc nghiệm kèm theo đáp án chắc chắn sẽ giúp các bạn học sinh rèn luyện cách giải nhanh các bài tập Toán. Mời các bạn và thầy cô tham khảo.

Đề thi giữa học kì 1 môn Toán lớp 12, trường THPT Thuận Thành 3, Bắc Ninh, năm học 2017 - 2018

Đề khảo sát chất lượng môn Toán 12 trường THPT Đoàn Kết, Hai Bà Trưng, Hà Nội, năm học 2017 - 2018

Bộ đề thi học kì 1 môn Toán lớp 12 năm học 2016 - 2017 (Số 1)

Đề thi giữa học kì 1 môn Toán lớp 12, trường THPT Tây Hồ, Hà Nội, năm học 2017 - 2018

TRƯỜNG THPT TÂY HỒ

ĐỀ THI GIỮA HỌC KỲ I NĂM HỌC 2017 - 2018

Môn thi: TOÁN

Thời gian làm bài: 60 phút, không kể thời gian giao đề

Câu 1. Hàm số _{$y\ =\ \frac{3x\ -1}{x+2}$}Có đạo hàm là:

^{A. $y'\ =\ \frac{-5}{\left(x+2\right)^2}$}

^{B. $y'\ =\ \frac{-7}{\left(x+2\right)^2}$}

C. $y'\ =\ \frac{5}{\left(x+2\right)^2}$

Câu 6. Tı̀m các giá tri ̣của tham số m để hàm số $y\ =\ -\frac{1}{3}x^3+2x^2-mx+2$ $y\ =\ -\frac{1}{3}x^3+2x^2-mx+2$ nghịch biến trên (-oo, +oo)

A) m ≥ 4

B) m ≤ 4

C) m > 4

D) m < 4

Câu 7. Cho hàm số $y\ =\ \frac{2x-3}{4-x}$ $y\ =\ \frac{2x-3}{4-x}$ Chọn phát biểu đúng trong các phát biểu sau.

A) Đồng biến trên R

B) Đồng biến trên từng khoảng xác định

C) Nghịch biến trên từng khoảng xác định

D) Luôn giảm trên R

Câu 8. Tı̀m tất cả các giá tri ̣của tham số m để hàm sô khoảng (0; + oo)

y = - x³ - x² + (m + 1)x + 2m nghich biến trên

A) m ≤ -1

B) m > -1

C) m ≤ 3

D) m > 3

Câu 9. Tìm tất cả các giá tri ̣của tham số m để hàm số $y\ =\ \frac{1}{2}x^3-mx^2\ +\ \left(m^2-m\ \ +1\right)x+1$ $y\ =\ \frac{1}{2}x^3-mx^2\ +\ \left(m^2-m\ \ +1\right)x+1$ đạt cực đại tại điểm có hoành độ bằng:

A. m= 0

B. m = -1

C. m = 2

D. m = 3

Câu 10. Khẳng định nào sau đây là đúng về hàm số y = x⁴ + 4x² + 2

A) Hàm số đaṭ cực tiểu tại x = 0

B) Hàm số có cực đaại và cực tiểu

C) Hàm số có cực đại và không có cực tiểu

D) Hàm số không có cực trị

Câu 11. Tı̀m tất cả các giá tri ̣của tham số m để hàm số

y = x⁴ - 2(m + 1)x² + m có ba cực tri.̣

A) m > 2

B) m > -1

C) m < 0

D) m < -1

Câu 12. Cho hàm số y = f ( x) xác định, liên tục trên tập R và có bảng biến thiên như hı̀nh vẽ sau.

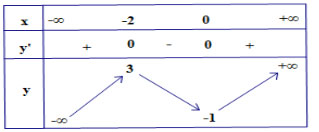
Trong các khẳng đinh sau, khẳng đinh sai là:

A) Hàm số đaṭ cưc đaị tai x = -2

B) Hàm số đồng biến trên khoảng (- oo;- 2); (0;+ oo)

C) Đồ thi ̣hàm số không có đường tiệm cận

D) Giá tri ̣nhỏ nhất của hàm số bằng - 1

Câu 13. Với giá trị nào của tham số m thì đồ thị hàm số y = x⁴ - 2(m - 1) x² + m⁴ - 3m² + 2017 có ba điểm cực trị tạo thành một tam giác có diện tích bằng 32?

A) m = 2

B) m = 3

C) m = 4

D) m = 5

Câu 14. Đồ thị hàm số nào sau đây có đường tiệm cận ngang là y = -2

A. $y\ =2+\frac{1}{x}$ $y\ =2+\frac{1}{x}$

B. $y=\ \frac{2x}{x+2}$ $y=\ \frac{2x}{x+2}$

C. $y=\frac{1-2x}{x+3}$ $y=\frac{1-2x}{x+3}$

D. $y=\ \frac{2x}{x^2+2}$ $y=\ \frac{2x}{x^2+2}$

Câu 16. Cho hàm sô y = f (x) có đồ thi ̣như hình bên.

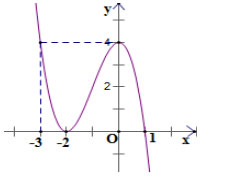
Đề thi giữa học kì 1 môn Toán lớp 12

Trong các mênh đề sau, mênh đề sai là:

A) Hàm số đạt cực tiểu tại x = -2

B) Hàm số đồng biến trên khoảng (-2;4)

C) Hàm số có hai cực trị

D) Đồ thi ̣hàm số và truc Ox có hai điểm chung

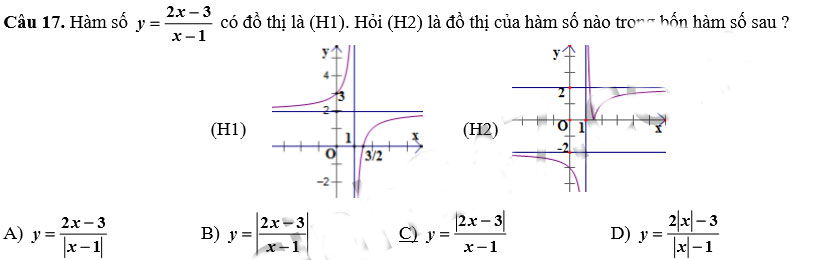
Đề thi giữa học kì 1 môn Toán lớp 12

Câu 18. Hàm số _{$y\ =\ \frac{x^3}{3}+\ \frac{x^2}{2}-2x\ -1$ có giá trị nhỏ nhất trên đoạn (0;2) bằng:}

A. $\frac{-1}{3}$ $\frac{-1}{3}$

B. 0

C. -1

D. $\frac{-13}{6}$ $\frac{-13}{6}$

Câu 19. Giá tri ̣nhỏ nhất m của hàm số $y\ =\ x+\frac{1}{x+2}$ $y\ =\ x+\frac{1}{x+2}$ trên (-1;2) là:

A. $m=\frac{9}{4}$ $m=\frac{9}{4}$

B. $m\ =-\frac{1}{2}$ $m\ =-\frac{1}{2}$

C. m= 2

D. m = 0

Câu 20. Tìm các giá tri ̣của tham số m để giá tri ̣nhỏ nhất của hàm số $y\ =\ \frac{x\ =m^2}{x+2}$ $y\ =\ \frac{x\ =m^2}{x+2}$ trên (0;2) bằng -1/2

A. $m\ =\ \pm\sqrt{3}$ $m\ =\ \pm\sqrt{3}$

B. $m=\sqrt{3}$ $m=\sqrt{3}$

C. m = 1

D. $m=\ \pm1$ $m=\ \pm1$

Câu 21. Gọi M và N là giao điểm của đường cong $y\ =\ \frac{7x+6}{x-2}$ $y\ =\ \frac{7x+6}{x-2}$ và đường thẳng y = x + 2. Khi đó hoành

A) 7

B) 3

C) - 7/2

D) 7/2

Câu 22. Số giao điểm của hai đồ thị y = x³ - x² - 2x + 3; y = x² - x + 1 là?

A) 0

B) 1

C) 3

D) 2

Câu 23. Đồ thi ̣hàm số y = x³ + 3x² + m cắt trục Ox tại ba điểm phân biệt thı̀ tập giá tri ̣của m là:

A) (-oo;- 4) υ (0;+oo)

B) (-4;0 )

C) (0; 4)

D) (0;+ oo)

Câu 24. Cho hình chóp S. ABC có đáy là tam giác ABC vuông tại B, AB = a , BC = $a\sqrt{2}$ $a\sqrt{2}$ . SA vuông góc với đáy, SA = 2a. Tính theo a thể tích V của khối chóp S. ABC

A. $V=\ \frac{a^3\sqrt{2}}{2}$ $V=\ \frac{a^3\sqrt{2}}{2}$

B. $V=\frac{a^3\sqrt{2}}{3}$ $V=\frac{a^3\sqrt{2}}{3}$

C. $V=\frac{a^3\sqrt{2}}{6}$ $V=\frac{a^3\sqrt{2}}{6}$

D. $V\ =\ \frac{a^3\sqrt{3}}{6}$ $V\ =\ \frac{a^3\sqrt{3}}{6}$

Câu 25. Cho hình chóp S.ABC đáy là tam giác vuông tại B, cạnh bên SA ⊥ (ABC). Biết SA = 3a, AB = 2a, BC = a. Thể tích V của khối chóp S.ABC là:

A) V = a³

B) V = 2a³

C) V = 3a³

D) V = 4a³

Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và

SA = a $\sqrt{3}$ $\sqrt{3}$. Tính thể tích V của khối chóp S.ABCD.

A. $V\ =\ \sqrt{3a^3}$ $V\ =\ \sqrt{3a^3}$

B. $V\ =\ \frac{\sqrt{3}}{6}a^3$ $V\ =\ \frac{\sqrt{3}}{6}a^3$

C. $V\ =\ \frac{\sqrt{3}}{3}a^3$ $V\ =\ \frac{\sqrt{3}}{3}a^3$

D. $V\ =\ \frac{\sqrt{3}}{9}a^3$ $V\ =\ \frac{\sqrt{3}}{9}a^3$

Câu 27. Khối chóp có diên tı́ch đaý là B và chiều cao là h thı̀ thể tích V của khối chóp đó là:

A) V = $\frac{1}{3}$ $\frac{1}{3}$ B.h

B) V = B.h

C) V = 3B.h

D) V = B.h²

Câu 28. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a. Góc giữa mặt bên và mặt đáy bằng 60⁰.Tính theo a thể tích khối chóp S.ABCD.

A. $V=\ \frac{4a^3\sqrt{3}}{3}$ $V=\ \frac{4a^3\sqrt{3}}{3}$

B. $V\ =\ \frac{a^3\sqrt{3}}{3}$ $V\ =\ \frac{a^3\sqrt{3}}{3}$

C. $V=\frac{2a^3\sqrt{6}}{3}\$ $V=\frac{2a^3\sqrt{6}}{3}\ $

D. $V=\ \frac{4a^3\sqrt{6}}{3}$ $V=\ \frac{4a^3\sqrt{6}}{3}$

Câu 29. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy, cạnh bên SC tạo với đáy góc 60⁰. Thể tích khối chóp đã cho bằng:

A. $V\ =\ \frac{4a^3\sqrt{6}}{3}$ $V\ =\ \frac{4a^3\sqrt{6}}{3}$

B. $V=\ \frac{a^3\sqrt{6}}{3}$ $V=\ \frac{a^3\sqrt{6}}{3}$

C. $V=\ \frac{2a^3\sqrt{6}}{3}$ $V=\ \frac{2a^3\sqrt{6}}{3}$

D. $V=\frac{4a^3\sqrt{2}}{3}$ $V=\frac{4a^3\sqrt{2}}{3}$

Câu 30. Cho hình chóp tứ giác đều (H) có diện tích đáy bằng 4 và diện tích của một mặt bên bằng $\sqrt{2}$ $\sqrt{2}$ . Thể tích V của (H) là:

A. $V\ =\ \frac{4\sqrt{3}}{3}$ $V\ =\ \frac{4\sqrt{3}}{3}$

B. V = 4

C. $V\ =\frac{4}{3}$ $V\ =\frac{4}{3}$

D. $V\ =\frac{4\sqrt{2}}{3}$ $V\ =\frac{4\sqrt{2}}{3}$

Câu 31. Cho hình chóp S.ABCD có đáy là hình vuông có cạnh a. Mặt bên SAB là tam giác đều nằm trong mặt phẳng vuông góc với đáy (ABCD). Tính thể tích V khối chóp S.ABCD?

A. $V\ =\ \frac{a^3\sqrt{3}}{6}$ $V\ =\ \frac{a^3\sqrt{3}}{6}$

B. $V\ =\ a^3\sqrt{3}$ $V\ =\ a^3\sqrt{3}$

C. $V=\ \frac{a^3\sqrt{3}}{2}$ $V=\ \frac{a^3\sqrt{3}}{2}$

D. $V=\ \frac{a^3\sqrt{3}}{3}$ $V=\ \frac{a^3\sqrt{3}}{3}$

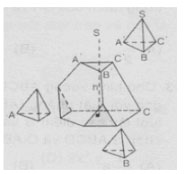
Câu 32. Cho một tứ diện đều có chiều cao h. Ở ba góc của tứ diện người ta cắt đi các tứ diện đều bằng nhau có chiều cao x để khối đa diện còn lại có thể tích bằng một nửa thể tích tứ diện đều ban đầu (hình bên ). Giá trị của x là bao nhiêu?

A. $x=\ \frac{h}{\sqrt[3]{2}}$ $x=\ \frac{h}{\sqrt[3]{2}}$

B. $x=\frac{h}{\sqrt[3]{3}}$ $x=\frac{h}{\sqrt[3]{3}}$

C. $x=\ \frac{h}{\sqrt[3]{4}}$ $x=\ \frac{h}{\sqrt[3]{4}}$

D. $x=\frac{h}{\sqrt[3]{6}}$ $x=\frac{h}{\sqrt[3]{6}}$

Câu 33. Cho hı̀nh chóp S.ABC có đáy ABC là tam đều canh a, SA ^ (ABC). Góc giữa SB và đáy bằng 60^0. Khoảng cách d giữa AC và SB là:

A. d = 2a

B. $d=\ \frac{\sqrt{2}}{2}a$ $d=\ \frac{\sqrt{2}}{2}a$

C. $d\ =\ \frac{\sqrt{15}}{15}a$ $d\ =\ \frac{\sqrt{15}}{15}a$

D. $d\ =\ \frac{\sqrt{7}}{7}a$ $d\ =\ \frac{\sqrt{7}}{7}a$

Chia sẻ, đánh giá bài viết

1

740