Đề thi học sinh giỏi giải toán trên máy tính bỏ túi lớp 11 trường THPT Lê Quý Đôn, Thái Nguyên năm học 2015 - 2016
Đề thi học sinh giỏi giải toán trên máy tính bỏ túi lớp 11
Đề thi học sinh giỏi giải toán trên máy tính bỏ túi lớp 11 trường THPT Lê Quý Đôn, Thái Nguyên năm học 2015 - 2016 được VnDoc.com sưu tầm và giới thiệu tới quý thầy cô và các em học sinh tham khảo. Đề thi giải toán trên máy tính cầm tay lớp 11 có đáp án đi kèm, hi vọng sẽ giúp các bạn ôn tập hiệu quả nhằm sẵn sàng cho kỳ thi học sinh giỏi lớp 11 được tốt nhất.
Đề thi giải toán trên máy tính cầm tay lớp 11 THPT tỉnh Thái Nguyên năm 2011 - 2012
Đề thi giải toán trên Máy tính cầm tay tỉnh Vĩnh Phúc năm 2010 - 2011 môn Toán THPT
TRƯỜNG LÊ QUÝ ĐÔN THÁI NGUYÊN | KỲ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG GIẢI TOÁN TRÊN MÁY TÍNH BỎ TÚI LỚP 11 NĂM HỌC 2015 - 2016 | ||||
ĐỀ CHÍNH THỨC |
| Thời gian: 150 phút (không kể thời gian giao đề) | |||
| Ngày thi: 10/3/2016. | ||||
Chú ý
- Thí sinh được sử dụng một trong các loại máy tính Casio fx-570MS, ES PLUS; Casio fx-500 VNPLUS; Vinacal Vn-500MS, 570MS và Vinacal-570MS New.
- Nếu không nói gì thêm hãy tính chính xác đến 4 chữ số sau dấu phẩy.
- Đề thi gồm có 06 trang. Thí sinh làm bài trực tiếp vào đề thi này.
Bài 1 (5 điểm). Với n là số tự nhiên khác 0, ký hiệu [a] là giá trị phần nguyên của số a.
Tính tổng 
Bài 2 (5 điểm). Cho đường thẳng (∆m) có phương trình: 
, trong đó m là tham số. Tìm tọa độ điểm M mà (∆m) luôn đi qua với mọi giá trị của m.
Bài 3 (5 điểm). Tìm giá trị nhỏ nhất của biểu thức: 
Bài 4 (5 điểm). Cho dãy số (un), biết và 
, với n ∈ N, n ≥ 2.
a) Lập quy trình ấn phím để tính giá trị của (un).
b) Tính gần đúng giá trị (un).
Bài 5 (5 điểm). Biết n là số tự nhiên sao cho giá trị của biểu thức (1 + √1)(2 + √2)...(n + √n) sai khác số 195554665 không quá một đơn vị. Hãy tìm hệ số của số hạng chứa x5 trong khai triển biểu thức (3 + 2x -x2)n thành đa thức.
Bài 6 (5 điểm). Tìm ba chữ số cuối của số M, biết M = 292016.
Bài 7 (5 điểm). Tính giá trị lớn nhất và giá trị nhỏ nhất của hàm số 
trên đoạn [0; 10].
Bài 8 (5 điểm). Tính gần đúng diện tích tứ giác ABCD với toạ độ các đỉnh A(1; 2); B(3; -2√2); C(-√2; -4); D(-2√2; 5).
Bài 9 (5 điểm). Một hộp đựng 20 viên bi màu xanh, 5 viên bi màu đỏ (các viên bi đều giống nhau về khối lượng và kích thước). Cần phải bốc ngẫu nhiên trong hộp đó một lần ít nhất là bao nhiêu viên bi, để xác suất có viên bi đỏ trong lần bốc đó lớn hơn 0,9595.
Bài 10 (5 điểm). Tính gần đúng giá trị của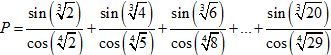 
Đáp án đề thi học sinh giỏi giải toán trên máy tính bỏ túi lớp 11
