Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 11 Toán 11 Lý thuyết Toán 11
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Trắc nghiệm Toán 11 Ứng dụng đạo hàm (mức độ vận dụng cao)

Bài tập Toán 11 Đạo hàm có đáp án

Dạng bài vận dụng cao ứng dụng đạo hàm lớp 11

Ứng dụng đạo hàm là một chuyên đề quan trọng trong chương trình Toán 11, yêu cầu học sinh nắm chắc kiến thức lý thuyết và khả năng vận dụng linh hoạt vào bài toán thực tế. Bộ Trắc nghiệm Toán 11 Ứng dụng đạo hàm (mức độ vận dụng cao) dưới đây được biên soạn chọn lọc với nhiều dạng bài phân loại, giúp học sinh làm quen với các câu hỏi khó, dạng nâng cao, rèn kỹ năng tư duy, phân tích và xử lý nhanh trong phòng thi. Mỗi câu hỏi đều có đáp án chi tiết, giúp bạn tự học, tự kiểm tra và ôn tập hiệu quả trước các kỳ thi quan trọng.

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 16 câu
  • Điểm số bài kiểm tra: 16 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Vận dụng cao
    Tính tổng tất cả các phần tử của S

    Cho hàm số y = - x^{3} + 4x^{2} + 1 có đồ thị là (C) và điểm M(m;1). Gọi S là tập hợp tất cả các giá trị thực của m để qua M kẻ được đúng 2 tiếp tuyến đến đồ thị (C). Tổng giá trị tất cả các phần tử của S bằng:

    Hướng dẫn:

    Phương trình tiếp tuyến của đồ thị (C) đi qua M(m;1) và có hệ số góc k là: y = k(x - m) + 1.

    Để qua M kẻ được đúng 2 tiếp tuyến đến đồ thị (C) điều kiện là hệ phương trình sau có đúng hai nghiệm x phân biệt

    (I):\left\{ \begin{matrix} - x^{3} + 4x^{2} + 1 = k(x - m) + 1 \\ \left( - x^{3} + 4x^{2} + 1 \right)' = k \end{matrix} \right. \Leftrightarrow \left\{ \begin{matrix} - x^{3} + 4x^{2} + 1 = k(x - m) + 1\ \ \ \ (1) \\ - 3x^{2} + 8x = k\ \ \ \ (2) \end{matrix} \right.

    Thay (2) vào (1) ta được

    - x^{3} + 4x^{2} + 1 = \left( - 3x^{2} + 8x \right)(x - m) + 1\Leftrightarrow x\left\lbrack 2x^{2} - (3m + 4)x + 8m \right\rbrack = 0

    \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ 2x^{2} - (3m + 4)x + 8m = 0\ \ \ (3) \end{matrix} \right.

    Như vậy, hệ (I) có đúng hai nghiêm khi và chỉ khi phương trình (3) có một nghiệm bằng 0 và một nghiệm khác 0; hoặc phương trình (3) có nghiệm duy nhất khác 0.

    Phương trình (3) có nghiệm x = 0 khi và chỉ khi m = 0.

    Khi đó, phương trình (3) trở thành: 2x^{2} - 4x = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 2 \end{matrix} \right.;

    Do đó m = 0 thỏa mãn.

    Phương trình (3) có nghiệm duy nhất khác 0 điều kiện là

    \left\{ \begin{matrix}\Delta = (3m + 4)^{2} - 4.2.8m = 0 \\\dfrac{3m + 4}{4} \neq 0\end{matrix} \right.

    \Leftrightarrow \left\{ \begin{matrix}\Delta = (3m + 4)^{2} - 4.2.8m = 0 \\\dfrac{3m + 4}{4} \neq 0\end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix}m = 4 \\m = \dfrac{4}{9}\end{matrix} \right..

    Như vậy S = \left\{ 0;\frac{4}{9};4 \right\}.

    Tổng giá trị tất cả các phần tử của S là 0 + \frac{4}{9} + 4 = \frac{40}{9}.

  • Câu 2: Vận dụng cao
    Tìm giá trị nhỏ nhất của tham số m thỏa mãn yêu cầu

    Cho hàm số y = \frac{x + 1}{2x - 1} có đồ thị hàm số (C).Tìm giá trị nhỏ nhất của m sao cho tồn tại ít nhất một điểm M thuộc  (C) mà tiếp tuyến của (C) tại M tạo với hai trục toạ độ một tam giác có trọng tâm nằm trên đường thẳng d:y = 2m - 1.

    Hướng dẫn:

    Gọi M(x_{0};y_{0}) \in (C).

    Phương trình tiếp tuyến tại M: y = \frac{- 3}{(2x_{0} - 1)^{2}}(x - x_{0}) + y_{0}

    Gọi A, B là giao điểm của tiếp tuyến với trục hoành và trục tung y_{B} = \frac{2x_{0}^{2} + 4x_{0} - 1}{(2x_{0} - 1)^{2}}.

    Từ đó trọng tâm G của \Delta OAB có: y = 3x - \frac{1}{3}.

    Vì G \in d nên \frac{2x_{0}^{2} + 4x_{0} - 1}{3(2x_{0} - 1)^{2}} = 2m - 1

    Mặt khác: \frac{2x_{0}^{2} + 4x_{0} - 1}{(2x_{0} - 1)^{2}} = \frac{6x_{0}^{2} - (2x_{0} - 1)^{2}}{(2x_{0} - 1)^{2}} = \frac{6x_{0}^{2}}{(2x_{0} - 1)^{2}} - 1 \geq - 1

    Do đó để tồn tại ít nhất một điểm M thỏa bài toán thì 2m - 1 \geq - \frac{1}{3} \Leftrightarrow m \geq \frac{1}{3}.

    Vậy giá trị nhỏ nhất của tham số m là \frac{1}{3}.

  • Câu 3: Vận dụng cao
    Chọn kết quả chính xác

    Tìm tất cả các giá trị thực của tham số m để đường thẳng y = - 2x + m cắt đồ thị (H) của hàm số y = \frac{2x + 3}{x + 2} tại hai điểm A,\ B phân biệt sao cho P = k_{1}^{2018} + k_{2}^{2018} đạt giá trị nhỏ nhất, với k_{1},k_{2} là hệ số góc của tiếp tuyến tại A,\ B của đồ thị (H).

    Hướng dẫn:

    Phương trình hoành độ giao điểm \frac{2x + 3}{x + 2} = - 2x + m

    \Leftrightarrow \left\{ \begin{matrix} x \neq - 2 \\ (x + 2)(2x - m) + 2x + 3 = 0 \end{matrix} \right. \Leftrightarrow \left\{ \begin{matrix} x \neq - 2 \\ 2x^{2} - (m - 6)x + 3 - 2m = 0\ \ \ \ \ \ (1) \end{matrix} \right.

    Đường thẳng d:y = - 2x + m cắt (H) tại hai điểm phân biệt

    \Leftrightarrow có 2 nghiệm phân biệt khác - 2

    \Leftrightarrow \left\{ \begin{matrix} \Delta = (m - 6)^{2} - 8(3 - 2m) > 0 \\ 2.( - 2)^{2} - (m - 6).( - 2) + 3 - 2m \neq 0 \end{matrix} \right.

    Khi đó x_{A},\ x_{B} là 2 nghiệm phân biệt của \Rightarrow \left\{\begin{matrix}x_{A} + x_{B} = \dfrac{m - 6}{2} \\x_{A}x_{B} = \dfrac{3 - 2m}{2}\end{matrix} \right.

    Ta có:

    y' = \frac{1}{(x + 2)^{2}} \Rightarrow k_{1} = \frac{1}{\left( x_{A} + 2 \right)^{2}},\ k_{2} = \frac{1}{\left( x_{B} + 2 \right)^{2}}

    \Rightarrow k_{1}k_{2} =\dfrac{1}{\left\lbrack 2\left( x_{A} + x_{B} \right) + x_{A}x_{B} + 4\right\rbrack^{2}} = \frac{1}{\left( m - 6 + \dfrac{3 - 2m}{2} + 4\right)^{2}} = 4

    \Rightarrow P = k_{1}^{2018} + k_{2}^{2018} \geq 2\sqrt{k_{1}^{2018}k_{2}^{2018}} = 2\sqrt{4^{2018}}

    Dấu "=" xảy ra \Leftrightarrow k_{1} = k_{2} > 0

    \Leftrightarrow \frac{1}{\left( x_{A} + 2 \right)^{2}} = \frac{1}{\left( x_{B} + 2 \right)^{2}} \Leftrightarrow \left\lbrack \begin{matrix} x_{A} + 2 = x_{B} + 2 \\ x_{A} + 2 = - \left( x_{B} + 2 \right) \end{matrix} \right.

    Do \left\{ \begin{matrix} A \neq B \\ A,\ B \in (H) \end{matrix} \right.\ \Rightarrow x_{A} \neq x_{B}

    \Leftrightarrow x_{A} + x_{B} = - 4.

    Kết hợp với ta được \frac{m - 6}{2} = - 4 \Leftrightarrow m = - 2 thỏa mãn.

  • Câu 4: Vận dụng cao
    Chọn đáp án đúng

    Cho hàm số y = \frac{x^{2} + 2mx + 2m^{2} - 1}{x - 1} \left( C_{m} \right) với m là tham số. Tìm tất cả các giá trị thực của tham số m sao cho \left( C_{m} \right) cắt trục hoành tại hai điểm phân biệt và các tiếp tuyến với \left( C_{m} \right) tại hai điểm này vuông góc với nhau.

    Hướng dẫn:

    Hàm số đã cho xác định trên \mathbb{R}\backslash\left\{ 1 \right\}.

    Xét phương trình hoành độ giao điểm của \left( C_{m} \right) và trục hoành:

    \frac{x^{2} + 2mx + 2m^{2} - 1}{x - 1} =0\Leftrightarrow x^{2} + 2mx + 2m^{2} - 1 = 0,\mathbf{\ }(x \neq1) (1)

    Để \left( C_{m} \right) cắt trục hoành tại hai điểm phân biệt A,B thì phương trình (1) phải có hai nghiệm phân biệt khác 1.

    Tức là ta phải có: \left\{ \begin{matrix} \Delta' = m^{2} - 2m^{2} + 1 > 0 \\ 1 + 2m + 2m^{2} - 1 \neq 0 \end{matrix} \right. hay \left\{ \begin{matrix} (1 - m)(1 + m) > 0 \\ 2m(m + 1) \neq 0 \end{matrix} \right. tức \left\{ \begin{matrix} - 1 < m < 1 \\ m \neq 0 \end{matrix} \right. (2).

    Gọi x_{1};x_{2} là hai nghiệm của (1).

    Theo định lý Vi – ét, ta có: \left\{ \begin{matrix} x_{1} + x_{2} = - 2m \\ x_{1}.x_{2} = 2m^{2} - 1 \end{matrix} \right.

    Giả sử I\left( x_{0};0 \right) là giao điểm của \left( C_{m} \right) và trục hoành.

    Tiếp tuyến của \left( C_{m} \right) tại điểm I có hệ số góc

    y'\left( x_{0} \right) = \frac{\left( 2x_{0} + 2m \right)\left( x_{0} - 1 \right) - \left( x_{0}^{2} + 2mx_{0} + 2m^{2} - 1 \right)}{\left( x_{0} - 1 \right)^{2}} = \frac{2x_{0} + 2m}{x_{0} - 1}

    Như vậy, tiếp tuyến tại A,B lần lượt có hệ số góc là:

    y'\left( x_{1} \right) = \frac{2x_{1} + 2m}{x_{1} - 1} và y'\left( x_{2} \right) = \frac{2x_{2} + 2m}{x_{2} - 1}.

    Tiếp tuyến tại A,B vuông góc nhau khi và chỉ khi y'\left( x_{1} \right)y'\left( x_{2} \right) = - 1 hay \left( \frac{2x_{1} + 2m}{x_{1} - 1} \right)\left( \frac{2x_{2} + 2m}{x_{2} - 1} \right) = - 1

    \Leftrightarrow 5x_{1}.x_{2} + (4m - 1)\left( x_{1} + x_{2} \right) + 4m^{2} + 1 = 0

    Tức 3m^{2} + m - 2 = 0 \Leftrightarrow m = - 1 hoặc m = \frac{2}{3}.

    Đối chiếu điều kiện chỉ có m = \frac{2}{3} thỏa mãn.

  • Câu 5: Vận dụng cao
    Tính diện tích tam giác

    Biết với một điểm M tùy ý thuộc (C):y = \frac{x^{2} + 3x + 3}{x + 2}, tiếp tuyến tại M cắt (C) tại hai điểm A,B tạo với I( - 2; - 1) một tam giác có diện tích không đổi, diện tích tam giác đó là?

    Hướng dẫn:

    Ta có: y = \frac{x^{2} + 3x + 3}{x + 2} = x + 1 + \frac{1}{x + 2}.

    Ta có: y' = 1 - \frac{1}{(x + 2)^{2}}.

    Gọi M\left( x_{0};y_{0} \right) \in (C) \Rightarrow y_{0} = x_{0} + 1 + \frac{1}{x_{0} + 2}(*)

    Tiếp tuyến với (C) tại M là \Delta:y = \left\lbrack 1 - \frac{1}{\left( x_{0} + 2 \right)^{2}} \right\rbrack\left( x - x_{0} \right) + x_{0} + 1 + \frac{1}{x_{0} + 2}

    Nếu \Delta \cap x = - 2 tại điểm A, thì y_{A} = - \frac{x_{0}}{x_{0} + 2} \Rightarrow A\left( - 2; - \frac{x_{0}}{x_{0} + 2} \right)

    Nếu \Delta cắt tiệm cận xiên tại điểm B thì:

    \left\lbrack 1 - \frac{1}{\left( x_{0} + 2 \right)^{2}} \right\rbrack\left( x_{B} - x_{0} \right) + x_{0} + 1 + \frac{1}{x_{0} + 2} = x_{B} + 1

    \Leftrightarrow x_{B} = 2x_{0} + 2 \Rightarrow y_{B} = x_{B} + 1 = 2x_{0} + 3

    \Rightarrow B\left( 2x_{0} + 2;2x_{0} + 3 \right)

    Nếu I là giao hai tiệm cận, thì I có tọa độ I( - 2; - 1).

    Gọi H là hình chiếu vuông góc của B trên tiệm cận đứng x = - 2 suy ra H( - 2;2x_{0} + 3)

    Diện tích tam giác AIB:

    S = \frac{1}{2}AI.BH = \frac{1}{2}\left|y_{A} - y_{I} \right|.\left| x_{B} - x_{H} \right|= \frac{1}{2}\left| -\frac{x_{0}}{x_{0} + 2} + 1 \right|\left| 2x_{0} + 2 + 2\right|

    Hay S = \frac{1}{2}\frac{2}{\left| x_{0} + 2 \right|}.2\left| x_{0} + 2 \right| = 2

    Chứng tỏ S là một hằng số, không phụ thuộc vào vị trí của điểm M.

  • Câu 6: Vận dụng cao
    Chọn đáp án đúng

    Cho hàm số y = x^{4} - 2mx^{2} + m, có đồ thị (C) với m là tham số thực. Gọi A là điểm thuộc đồ thị (C) có hoành độ bằng 1. Tìm m để tiếp tuyến \Delta với đồ thị (C) tại A cắt đường tròn (\gamma):\ x^{2} + (y - 1)^{2} = 4 tạo thành một dây cung có độ dài nhỏ nhất

    Hướng dẫn:

    Đường tròn (\gamma):\ x^{2} + (y - 1)^{2} = 4 có tâm I(0;\ 1), R = 2.

    Ta có A(1;\ 1 - m); y' = 4x^{3} - 4mx \Rightarrow y'(1) = 4 - 4m.

    Suy ra phương trình \Delta: y = (4 - 4m)(x - 1) + 1 - m.

    Dễ thấy \Delta luôn đi qua điểm cố định F\left( \frac{3}{4};\ 0 \right) và điểm F nằm trong đường tròn (\gamma).

     

    Giả sử \Delta cắt (\gamma) tại M, N.

    Thế thì ta có: MN = 2\sqrt{R^{2} - d^{2}(I;\ \Delta)} = 2\sqrt{4 - d^{2}(I;\ \Delta)}.

    Do đó MN nhỏ nhất \Leftrightarrow d(I;\ \Delta) lớn nhất \Leftrightarrow d(I;\ \Delta) = IF \Rightarrow \Delta\bot IF.

    Khi đó đường \Delta có 1 vectơ chỉ phương \overrightarrow{u}\bot\overrightarrow{IF} = \left( \frac{3}{4};\ - 1 \right); \overrightarrow{u} = (1;\ \ 4 - 4m) nên ta có:

    \overrightarrow{u}.\overrightarrow{n} = 0\Leftrightarrow 1.\frac{3}{4} - (4 - 4m) = 0 \Leftrightarrow m =\frac{13}{16}.

  • Câu 7: Vận dụng cao
    Tìm số giá trị k thỏa mãn yêu cầu bài toán

    Cho hàm số y = f(x) = x^{3} + 6x^{2} + 9x + 3\ \ (C). Tồn tại hai tiếp tuyến của (C) phân biệt và có cùng hệ số góc k, đồng thời đường thẳng đi qua các tiếp điểm của hai tiếp tuyến đó cắt các trục Ox,\ \ Oy tương ứng tại A và B sao cho OA = 2017.OB. Hỏi có bao nhiêu giá trị của k thỏa mãn yêu cầu bài toán?

    Hướng dẫn:

    Gọi M_{1}\left( x_{1};f\left( x_{1} \right) \right); M_{2}\left( x_{2};f\left( x_{2} \right) \right) với là hai tiếp điểm mà tại đó tiếp tuyến có cùng hệ số góc.

    Ta có y' = 3x^{2} + 12x + 9

    Khi đó :

    k = 3x_{1}^{2} + 12x_{1} + 9 = 3x_{2}^{2} + 12x_{2} + 9

    \Leftrightarrow \left( x_{1} - x_{2} \right)\left( x_{1} + x_{2} + 4 \right) = 0

    \Leftrightarrow x_{1} + x_{2} = - 4 = S(1)

    Hệ số góc của đường thẳng M_{1}M_{2} là:

    k' = \pm \frac{OB}{OA} = \pm \frac{1}{2017} = \frac{f\left( x_{2} \right) - f\left( x_{1} \right)}{x_{2} - x_{1}}

    \Leftrightarrow \pm \frac{1}{2017} = \left( x_{1} + x_{2} \right)^{2} - x_{1}x_{2} + 6\left( x_{1} + x_{2} \right) + 9

    \Leftrightarrow \left\lbrack\begin{matrix}x_{1}x_{2} = \dfrac{2016}{2017} = P \\x_{1}x_{2} = \dfrac{2018}{2017} = P\end{matrix} \right.\ (2)

    Với \left\{ \begin{matrix}x_{1} + x_{2} = - 4 = S \\x_{1}x_{2} = \dfrac{2016}{2017} = P\end{matrix} \right., do S^{2} > 4P nên \exists hai cặp x_{1},x_{2} \Rightarrow \exists 1 giá trị k

    Với \left\{ \begin{matrix}x_{1} + x_{2} = - 4 = S \\x_{1}x_{2} = \dfrac{2018}{2017} = P\end{matrix} \right., do S^{2} > 4P nên \exists hai cặp x_{1},x_{2} \Rightarrow \exists 1 giá trị k

    Vậy có tất cả 2 giá trị kthỏa mãn yêu cầu đề bài.

  • Câu 8: Vận dụng cao
    Tìm điểm cố định đường thẳng luôn đi qua

    Gọi M, N là hai điểm di động trên đồ thị (C) của hàm số y = - x^{3} + 3x^{2} - x + 4 sao cho tiếp tuyến của (C) tại M và N luôn song song với nhau. Khi đó đường thẳng MN luôn đi qua điểm cố định nào dưới đây?

    Hướng dẫn:

    Gọi tọa độ điểm M, N lần lượt là M\left( x_{1};y_{1} \right),\ N\left( x_{2};y_{2} \right).

    Hệ số góc tiếp tuyến của (C) tại M và N lần lượt là:

    k_{1} = y'\left( x_{1} \right) = - 3{x_{1}}^{2} + 6x_{1} - 1

    k_{2} = y'\left( x_{2} \right) = - 3{x_{2}}^{2} + 6x_{2} - 1

    Để tiếp tuyến của (C) tại M và N luôn song song với nhau điều kiện là:

    \left\{ \begin{matrix} k_{1} = k_{2} \\ x_{1} \neq x_{2} \end{matrix} \right. \Leftrightarrow \left\{ \begin{matrix} \left( x_{1} - x_{2} \right)\left\lbrack - 3\left( x_{1} + x_{2} \right) + 6 \right\rbrack = 0 \\ x_{1} \neq x_{2} \end{matrix} \right.

    \Leftrightarrow x_{1} + x_{2} = 2.

    Ta có:

    y_{1} + y_{2} = - \left( x_{1} +x_{2} \right)\left\lbrack \left( x_{1} + x_{2} \right)^{2} - 3x_{1}x_{2}\right\rbrack+ 3\left\lbrack \left( x_{1} + x_{2} \right)^{2} -2x_{1}x_{2} \right\rbrack - \left( x_{1} + x_{2} \right) +8

    Do x_{1} + x_{2} = 2 nên y_{1} + y_{2} = - 2\left( 4 - 3x_{1}x_{2} \right) + 3\left( 4 - 2x_{1}x_{2} \right) + 8 = 10.

    Trung điểm của đoạn MN là I(1;5).

    Vậy đường thẳng MN luôn đi qua điểm cố định I(1;5).

  • Câu 9: Vận dụng cao
    Chọn kết luận đúng

    Cho hàm số y = f(x) có đạo hàm tại x = 1. Gọi d_{1}, d_{2} lần lượt là tiếp tuyến của đồ thị hàm số y = f(x) và y = g(x) = xf(2x - 1) tại điểm có hoành độ x = 1. Biết rằng hai đường thẳng d_{1}, d_{2} vuông góc với nhau, khẳng định nào sau đây đúng

    Hướng dẫn:

    Ta có: g'\left( x \right) = f\left( {2x - 1} \right) + 2x.f'\left( {2x - 1} \right)

    \Rightarrow g'(1) = f(1) + 2f'(1).

    d_{1} có hệ số góc là f'(1).

    d_{2} có hệ số góc là g'(1) = f(1) + 2f'(1).

    Mà d_{1}\bot d_{2} \Rightarrow f'(1).g'(1) = - 1

    \Leftrightarrow f'(1).\left\lbrack f'(1) + 2f(1) \right\rbrack = - 1

    \Leftrightarrow f(1) = \frac{- 2\left\lbrack f'(1) \right\rbrack^{2} - 1}{f'(1)} \Rightarrow \left| f(1) \right| = \left| \frac{2\left\lbrack f'(1) \right\rbrack^{2} + 1}{f'(1)} \right|.

    Xét hàm số h(t) = \left| \frac{2t^{2} +1} {t} \right|

    Ta có bảng biến thiên như sau:

    Vậy h(t) \geq 2\sqrt{2} \forall t \neq 0 \Rightarrow \left| f(1) \right| \geq 2\sqrt{2}.

    Cách khác: Xét h(t) = \left| \frac{2t^{2} + 1}{t} \right|

    Với t > 0 ta có: \left| \frac{2t^{2} + 1}{t} \right| = \frac{2t^{2} + 1}{t} = 2t + \frac{1}{t} \geq 2\sqrt{2t.\frac{1}{t}} = 2\sqrt{2}.

    Với t < 0 ta có: \left| \frac{2t^{2} + 1}{t} \right| = - \frac{2t^{2} + 1}{t} = ( - 2t) + \left( - \frac{1}{t} \right) \geq 2\sqrt{( - 2t).\left( - \frac{1}{t} \right)} = 2\sqrt{2}.

    Vậy h(t) \geq 2\sqrt{2}\forall t \neq 0 \Rightarrow \left| f(1) \right| \geq 2\sqrt{2}.

  • Câu 10: Vận dụng cao
    Tính tổng tất cả các phần tử thuộc tập S

    Cho hàm số y = \frac{x + 1}{x - 1} có đồ thị (C) và điểm A(a;2). Gọi S là tập hợp tất cả các giá trị thực của a để có đúng hai tiếp tuyến của (C) đi qua điểm A và có hệ số góc k_{1}, k_{2} thỏa mãn k_{1} + k_{2} + 10{k_{1}}^{2}{k_{2}}^{2} = 0. Tổng giá trị tất cả các phần tử của S bằng

    Hướng dẫn:

    Ta có y' = \frac{- 2}{(x - 1)^{2}}.

    Gọi tọa độ tiếp điểm là M\left( t;\frac{t + 1}{t - 1} \right).

    Phương trình tiếp tuyến tại M là y = (x - t)\frac{- 2}{(t - 1)^{2}} + \frac{t + 1}{t - 1}.

    Do tiếp tuyến đi qua A(a;2) nên ta có;

    2 = (a - t)\frac{- 2}{(t - 1)^{2}} +\frac{t + 1}{t - 1}\Rightarrow t^{2} - 6t + 3 + 2a = 0 (1).

    Gọi t_{1}, t_{2} là hai nghiệm của (1) suy ra k_{1} = \frac{- 2}{\left( t_{1} - 1 \right)^{2}} và k_{2} = \frac{- 2}{\left( t_{2} - 1 \right)^{2}}.

    k_{1} + k_{2} + 10{k_{1}}^{2}{k_{2}}^{2} = 0

    \Leftrightarrow \frac{- 2}{\left( t_{1} - 1 \right)^{2}} + \frac{- 2}{\left( t_{2} - 1 \right)^{2}} + 10\frac{4}{\left( t_{1} - 1 \right)^{4}} \cdot \frac{4}{\left( t_{2} - 1 \right)^{4}} = 0

    \Rightarrow \left\lbrack \left( t_{1} - 1 \right)^{2} + \left( t_{2} - 1 \right)^{2} \right\rbrack\left( t_{1} - 1 \right)^{2}\left( t_{2} - 1 \right)^{2} = 80

    \Rightarrow \left\lbrack \left( t_{1} + t_{2} \right)^{2} - 2t_{1}t_{2} - 2\left( t_{1} + t_{2} \right) + 2 \right\rbrack\left\lbrack t_{1}t_{2} - t_{1} - t_{2} + 1 \right\rbrack^{2} = 80.

    Mặt khác theo Viète có t_{1} + t_{2} = 6 và t_{1}t_{2} = 3 + 2a.

    Thay vào ta có:

    (20 - 4a)(2a - 2)^{2} = 80

    \Rightarrow (5 - a)(a - 1)^{2} = 5\Rightarrow \left\lbrack \begin{matrix}a = 0 \\a = \dfrac{7 \pm \sqrt{5}}{2}\end{matrix} \right..

  • Câu 11: Vận dụng cao
    Tìm tọa độ điểm thỏa mãn yêu cầu bài toán

    Cho hàm số y = - x^{3} + 3x + 2 có đồ thị là (C). Tìm những điểm trên trục hoành sao cho từ đó kẻ được ba tiếp tuyến đến đồ thị hàm số và trong đó có hai tiếp tuyến vuông góc với nhau.

    Hướng dẫn:

    Xét điểm M(m;0) \in Ox.

    Cách 1: Đường thẳng d đi qua M, hệ số góc k có phương trình: y = k(x - m).

    d là tiếp tuyến của (C) \Leftrightarrowhệ \left\{ \begin{matrix} - x^{3} + 3x + 2 = k(x - m) \\ - 3x^{2} + 3 = k\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \end{matrix} \right. có nghiệm x

    Thế k vào phương trình thứ nhất, ta được:

    3(x^{2} - 1)(x - m) - (x^{3} - 3x - 2) = 0

    \Leftrightarrow (x + 1)(3x^{2} -3(1 +m)x + 3m) - (x + 1)(x^{2} - x - 2) = 0

    \Leftrightarrow (x + 1)\lbrack 2x^{2} - (3m + 2)x + 3m + 2\rbrack = 0(1)

    \Leftrightarrow x = - 1 hoặc 2x^{2} - (3m + 2)x + 3m + 2 = 0\ (2)

    Để từ M kẻ được ba tiếp tuyến thì (1) phải có nghiệm x, đồng thời phải có 3 giá trị k khác nhau, khi đó (2)phải có hai nghiệm phân biệt khác - 1, đồng thời phải có 2 giá trị k khác nhau và khác 0

    (2) phải có hai nghiệm phân biệt khác - 1 khi và chỉ khi:

    \left\{ \begin{matrix} \Delta = (3m + 2)(3m - 6) > 0 \\ 3m + 3 \neq 0 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} m < - \frac{2}{3},\ m > 2 \\ m \neq - 1 \end{matrix} \right. (3)

    Với điều kiện (3), gọi x_{1},x_{2} là hai nghiệm của (2), khi đó hệ số góc của ba tiếp tuyến là;

    k_{1} = - 3x_{1}^{2} + 3,\ k_{2} = - 3x_{2}^{2} + 3,\ k_{3} = 0.

    Để hai trong ba tiếp tuyến này vuông góc với nhau k_{1}.k_{2} = - 1 và k_{1} \neq k_{2}

    k_{1}.k_{2} = - 1 \Leftrightarrow 9(x_{1}^{2} - 1)(x_{2}^{2} - 1) = - 1

    \Leftrightarrow 9x_{1}^{2}x_{2}^{2} - 9(x_{1} + x_{2})^{2} + 18x_{1}x_{2} + 10 = 0\ (i)

    Mặt khác theo Định lí Viet \left\{\begin{matrix}x_{1} + x_{2} = \dfrac{3m + 2}{2} \\\ x_{1}x_{2} = \dfrac{3m + 2}{2}\end{matrix} \right..

    Do đó (i) \Leftrightarrow 9(3m + 2) + 10 = 0 \Leftrightarrow m = - \frac{28}{27} thỏa điều kiện (3), kiểm tra lại ta thấy k_{1} \neq k_{2}

    Vậy, M\left( - \frac{28}{27};0 \right) là điểm cần tìm.

    Cách 2: Gọi N(x_{0};y_{0}) \in (C).

    Tiếp tuyến \Delta của (C)tại N có phương trình: y = \left( - 3x_{0}^{2} + 3 \right)(x -x_{0}) +y_{0}.

    \Delta đi qua M \Leftrightarrow 0 =\left( - 3x_{0}^{2} + 3\right)(m - x_{0}) + y_{0}

    \Leftrightarrow 3(x_{0} - 1)(x_{0} + 1)(x_{0} - m) - (x_{0} + 1)^{2}(x_{0} - 2) = 0

    \Leftrightarrow \left( x_{0} + 1 \right)\left\lbrack 2x_{0}^{2} - (3m + 2)x_{0} + 3m + 2 \right\rbrack = 0

    \Leftrightarrow \left\lbrack \begin{matrix} x_{0} = - 1 \\ 2x_{0}^{2} - (3m + 2)x_{0} + 3m + 2 = 0\ \ \ (a) \end{matrix} \right.

    Từ M vẽ được đến (C) ba tiếp tuyến \Leftrightarrow (a) có hai nghiệm phân biệt khác - 1, và có hai giá trị k = - 3x_{0}^{2} + 3 khác nhau và khác 0 điều đó xảy ra khi và chỉ khi:

    \left\{ \begin{matrix} \Delta = (3m + 2)^{2} - 8(3m + 2) > 0 \\ 2 + 2(3m + 2) \neq 0 \end{matrix} \right.

    \Leftrightarrow \left\{ \begin{matrix} (3m + 2)(3m - 6) > 0 \\ 3m + 3 \neq 0 \end{matrix} \right.

    \Leftrightarrow \left\{ \begin{matrix}m \neq - 1 \\m <- \frac{2}{3},m > 2\end{matrix} \right. ( b ).

    Vì tiếp tuyến tại điểm có hoành độ x = - 1 có hệ số góc bằng 0 nên yêu cầu bài toán

    \Leftrightarrow ( - 3p^{2} + 3)( - 3q^{2} + 3) = -1

    \Leftrightarrow 9p^{2}q^{2} - 9(p^{2} + q^{2}) + 10 = 0

    \Leftrightarrow 9p^{2}q^{2} - 9(p + q)^{2} + 18pq + 10 = 0

    \Leftrightarrow \frac{9(3m + 2)^{2}}{4} - \frac{9(3m + 2)^{2}}{4} + 9(3m + 2) + 10 = 0

    \Leftrightarrow m = - \frac{28}{27}. Vậy M\left( -\frac{28}{27};0\right).

  • Câu 12: Vận dụng cao
    Tìm các giá trị tham số m thỏa mãn yêucầu

    Cho hàm số y = \frac{x^{2} - 2mx + m}{x + m}. Giá trị m để đồ thị hàm số cắt trục Ox tại hai điểm và tiếp tuyến của đồ thị tại hai điểm đó vuông góc là

    Hướng dẫn:

    Phương trình hoành độ giao điểm của đồ thị hàm số (C):\ y = \frac{x^{2} - 2mx + m}{x + m} và trục hoành:

    \frac{x^{2} - 2mx + m}{x + m} = 0 \Leftrightarrow \left\{ \begin{matrix} x^{2} - 2mx + m = 0\ \ (*) \\ x \neq - m \end{matrix} \right..

    Đồ thị hàm số y = \frac{x^{2} - 2mx + m}{x + m} cắt trục Ox tại hai điểm phân biệt \Leftrightarrow phương trình (*) có hai nghiệm phân biệt khác - m

    \Leftrightarrow \left\{ \begin{matrix} \Delta' = m^{2} - m > 0 \\ 3m^{2} + m \neq 0 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} m < 0\ \vee \ m > 1 \\ m \neq - \frac{1}{3} \end{matrix} \right..

    Gọi M\left( x_{0};\ y_{0} \right) là giao điểm của đồ thị (C) với trục hoành thì y_{0} = x_{0}^{2} - 2mx_{0} + m = 0 và hệ số góc của tiếp tuyến với (C) tại M là:

    k = y'\left( x_{0} \right) = \frac{\left( 2x_{0} - 2m \right)\left( x_{0} - 1 \right) - \left( x_{0}^{2} - 2mx_{0} + m \right)}{\left( x_{0} + m \right)^{2}} = \frac{2x_{0} - 2m}{x_{0} + m}.

    Vậy hệ số góc của hai tiếp tuyến với (C) tại hai giao điểm với trục hoành là;

    k_{1} = \frac{2x_{1} - 2m}{x_{1} + m}, k_{2} = \frac{2x_{2} - 2m}{x_{2} + m}.

    Hai tiếp tuyến này vuông góc \Leftrightarrow k_{1}.k_{2} = - 1

    \Leftrightarrow \left( \frac{2x_{1} - 2m}{x_{1} + m} \right)\left( \frac{2x_{2} - 2m}{x_{2} + m} \right) = - 1

    \Leftrightarrow 4\left\lbrack x_{1}x_{2} - m\left( x_{1} + x_{2} \right) + m^{2} \right\rbrack = - \left\lbrack x_{1}x_{2} + m\left( x_{1} + x_{2} \right) + m^{2} \right\rbrack\ \ (**).

    Ta lại có \left\{ \begin{matrix} x_{1}x_{2} = m \\ x_{1} + x_{2} = 2m \end{matrix} \right.. Do đó (**)

    \Leftrightarrow m^{2} - 5m = 0 \Leftrightarrow \left\lbrack \begin{matrix} m = 0 \\ m = 5 \end{matrix} \right..

    Nhận m = 5.

  • Câu 13: Vận dụng cao
    Tìm tập S

    Cho hàm số y = \frac{x + 2}{x - 1}(C) và điểm A(0;m). Giả sử S là tập hợp tất cả các giá trị của tham số m để từ A kẻ được 2 tiếp tuyến đến (C) sao cho hai tiếp điểm tương ứng nằm hai phía trục hoành. Tập S là:

    Hướng dẫn:

    Ta có y' = \frac{- 3}{(x - 1)^{2}}. Phương trình đường thẳng qua A(0;m) có hệ số góc k

    d:y = k(x - 0) + m. d là tiếp tuyến\Leftrightarrow Hệ phương trình: \left\{ \begin{matrix}\dfrac{x + 2}{x - 1} = kx + m \\k = \dfrac{- 3}{(x - 1)^{2}}\end{matrix} \right. có nghiệm.

    Thay k = \frac{- 3}{(x - 1)^{2}} vào \frac{x + 2}{x - 1} = kx + m ta được:

    (m - 1)x^{2} - 2(m + 2)x + m + 2 = 0(1).

    Để kẻ được 2 tiếp tuyến thì\ (1) có 2 nghiệm phân biệt x_{1}, x_{2} khác 1

    \Leftrightarrow \left\{ \begin{matrix} \Delta' = 3m + 6 > 0 \\ m \neq 1 \\ m - 1 - 2(m + 2) + m + 2 \neq 0 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} m > - 2 \\ m \neq 1 \end{matrix} \right..

    Hai tiếp điểm tương ứng nằm hai phía trục hoành khi y\left( x_{1} \right).y\left( x_{2} \right) < 0

    \Leftrightarrow \frac{x_{1} + 2}{x_{1} - 1}.\frac{x_{2} + 2}{x_{2} - 1} < 0 \Leftrightarrow \frac{P + 2S + 4}{P - S + 1} < 0

    \Leftrightarrow \frac{9m + 6}{- 3} < 0 \Leftrightarrow m > - \frac{2}{3}.

    Vậy \left\{ \begin{matrix}m > - \dfrac{2}{3} \\m \neq 1\end{matrix} \right..

  • Câu 14: Vận dụng cao
    Viết phương trình tiếp tuyến theo yêu cầu

    Lập phương trình tiếp tuyến với đồ thị hàm số y = f(x) thỏa mãn f^{2}(1 + 2x) = x - f^{3}(1 - x) tại điểm có hoành độ x = 1?

    Hướng dẫn:

    Ta có: f^{2}(1 + 2x) = x - f^{3}(1 - x).

    Suy ra 4.f(1 + 2x).f'(1 + 2x) = 1 + 3f^{2}(1 - x)f'(1 - x).

    Cho x = 0 ta đượcf^{2}(1) = - f^{3}(1), (1)

    và 4.f(1).f'(1) = 1 + 3f^{2}(1)f'(1), (2).

    Từ (1) suy ra f(1) = - 1 vì f(1) = 0 không thỏa mãn (2).

    Thay vào (2) ta được f'(1) = - \frac{1}{7}.

    Vậy phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ x = 1 là:

    y = f'(1)(x - 1) + f(1) hay y = - \frac{1}{7}x - \frac{6}{7}.

  • Câu 15: Vận dụng cao
    Định số giá trị nguyên của tham số m

    Cho hàm số y = x^{3} + x^{2} + 3x + 1 có đồ thị là (C). Có tất cả bao nhiêu giá trị nguyên của tham số m để từ điểm M(0;\ m) kẻ được ít nhất một tiếp tuyến đến đồ thị (C) mà hoành độ tiếp điểm thuộc đoạn \lbrack 1;\ 3\rbrack?

    Hướng dẫn:

    Ta có y' = 3x^{2} + 2x + 3.

    Gọi \left( x_{o};\ y_{0} \right) là tọa độ tiếp điểm.

    Phương trình tiếp tuyến có dạng:

    y = y'\left( x_{0} \right)\left( x - x_{0} \right) + y_{0} \Leftrightarrow y = \left( 3x_{0}^{2} + 2x_{0} + 3 \right)\left( x - x_{0} \right) + x_{0}^{3} + x_{0}^{2} + 3x_{0} + 1

    Vì tiếp tuyến qua M(0;\ m) nên ta có

    m = \left( 3x_{0}^{2} + 2x_{0} + 3\right)\left( 0 - x_{0} \right) + x_{0}^3 + x_{0}^{2} + 3x_{0} +1

    \Leftrightarrow m = - 2x_{0}^{3} - x_{0}^{2} + 1\ \ (1).

    Để từ điểm M(0;\ m) kẻ được ít nhất một tiếp tuyến đến đồ thị (C) mà hoành độ tiếp điểm thuộc đoạn \lbrack 1;\ 3\rbrackthì phương trình (1) có ít nhất một nghiệm x_{0} \in \lbrack 1;3\rbrack

    Xét hàm số y = f(t) = - 2t^{3} - t^{2} + 1 trên đoạn \lbrack 1;\ 3\rbrack suy ra f'(t) = - 6t^{2} - 2t = 0 \Leftrightarrow \left\lbrack \begin{matrix} t = 0 \\ t = - \frac{1}{3} \end{matrix} \right..

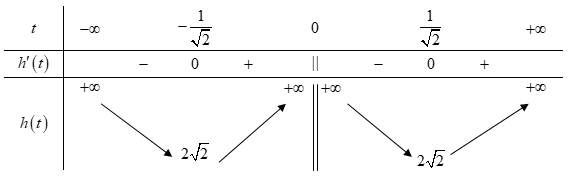
    Bảng biến thiên:

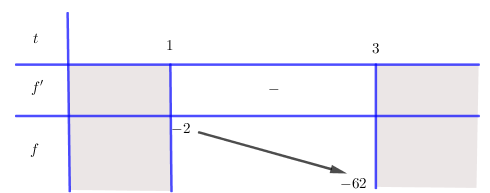
    Dựa vào bảng biến thiên ta có - 62 \leq m \leq - 2

    Vậy có tất cả 61 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.

  • Câu 16: Vận dụng cao
    Viết phương trình tiếp tuyến

    Cho hàm số y = - x - 1 có đồ thị (C). Viết phương trình tiếp tuyến của (C), biết tiếp tuyến tạo với hai trục tọa độ một tam giác có diện tích bằng x_{0}.

    Hướng dẫn:

    Hàm số xác định với mọi x \neq - 2.

    Ta có: y' = \frac{4}{{{{\left( {x + 2} \right)}^2}}}

    Gọi M(x_{0};y_{0}) \in (C). Tiếp tuyến y = 36x - 164 của (C) tại M có phương trình

    y = \frac{4}{(x_{0} + 2)^{2}}(x - x_{0})+ \frac{2x_{0}}{x_{0} + 2}= \frac{4}{(x_{0} + 2)^{2}}x +\frac{2x_{0}^{2}}{(x_{0} + 2)^{2}}

    Gọi A,\ B lần lượt là giao điểm của tiếp tuyến y = 15x + 39 với Ox,\ Oy

    Suy ra A:\left\{ \begin{matrix}y = 0 \\\frac{4}{(x_{0} + 2)^{2}}x + \frac{2x_{0}^{2}}{(x_{0} + 2)^{2}} = 0\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}x = - \dfrac{1}{2}x_{0}^{2} \\y = 0\end{matrix} \right.\ \Rightarrow A( -\dfrac{1}{2}x_{0}^{2};0)

    B:\left\{ \begin{matrix} x = 0 \\ y = \frac{2x_{0}^{2}}{(x_{0} + 2)^{2}} \end{matrix} \right.\ \Rightarrow B\left( 0;\frac{2x_{0}^{2}}{(x_{0} + 2)^{2}} \right)

    Vì A,B \neq O \Rightarrow x_{0} \neq 0.

    Tam giác AOB vuông tại O nên S_{\Delta AOB} = \frac{1}{2}OA.OB = \frac{1}{2}\frac{x_{0}^{4}}{(x_{0} + 2)^{2}}

    Suy ra S_{\Delta AOB} = \frac{1}{18} \Leftrightarrow \frac{x_{0}^{4}}{(x_{0} + 2)^{2}} = 9 \Leftrightarrow 9x_{0}^{4} = (x_{0} + 2)^{2}

    \Leftrightarrow \left\lbrack \begin{matrix} 3x_{0}^{2} + x_{0} + 2 = 0\ (vn) \\ 3x_{0}^{2} - x_{0} - 2 = 0 \end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix} x_{0} = 1 \\ x_{0} = - \frac{2}{3} \end{matrix} \right..

    Với x_{0} = 1 \Rightarrow y_{0} = \frac{2}{3},\ y'(x_{0}) = \frac{4}{9}. Suy ra phương trình \Delta:y = \frac{4}{9}x + \frac{2}{9}

    Với x_{0} = - \frac{2}{3} \Rightarrow y_{0} = - 1,\ y'(x_{0}) = \frac{9}{4} . Suy ra phương trình \Delta:y = \frac{9}{4}(x + \frac{2}{3}) - 1 = \frac{9}{4}x + \frac{1}{2}.

0/16
16 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (100%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
1
6 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này
🖼️

Lý thuyết Toán 11
Xem thêm