Đề thi giải toán trên Máy tính bỏ túi tỉnh Cà Mau môn Toán lớp 12 THPT năm học 2009 - 2010

Vndoc.com xin gửi đến các bạn: Đề thi giải toán trên Máy tính bỏ túi tỉnh Cà Mau môn Toán lớp 12 THPT năm học 2009 - 2010.

Đề thi môn Toán:

SỞ GIÁO DỤC VÀ ĐÀO TẠO CÀ MAU (Đề thi chính thức)

KỲ THI GIẢI TOÁN TRÊN MÁY TÍNH CẦM TAY NĂM HỌC 2009 - 2010 MÔN: TOÁN LỚP 12 THPT (Thời gian làm bài 150 phút không kể thời gian giao đề) Ngày thi: 29/11/2009

Bài 1:

Cho hàm số:

Tính:

Bài 2:

Trong mặt phẳng tọa độ (Oxy), cho đường tròn (C): x² + y² + 8x - 4y -5 = 0 và đường thẳng d: y = ax + b .Cho biết đường thẳng d đi qua điểm và tiếp xúc với đường tròn (C). Điểm A có thuộc đường tròn (C) không? Tính gần đúng giá trị của a và b.

Bài 3:

Tìm x (độ, phút, giây) thỏa mãn phương trình sau: 3(sin³x – cos³x) – 4sinxcosx = 1 (*)

Bài 4:

Tứ giác ABCD có các cạnh AB = 3dm, BC = 8dm, CD = 10dm, DA = 5dm. Tính gần đúng diện tích của tứ giác đó trong mỗi trường hợp sau:

a) Khi đường chéo BD = 6dm.

b) Khi AB//CD. Suy ra độ dài của bán kính đường tròn nội tiếp tứ giác trong trường hợp này.

Bài 5:

Cho 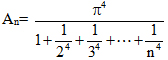. Tìm số tự nhiên n sao cho: 90,0113 < An < 90,018

Bài 6:

Hình tứ diện ABCD có AD vuông góc BC và AB = BC = CA = AD = DH = dm, trong đó DH là đường cao của tam giác BCD. Tính:

a) Bán kính R của đường tròn ngoại tiếp tam giác BCD.

b) Thể tích của khối tứ diện đó

c) Số đo (độ, phút, giây) của góc tạo bởi AC và mặt phẳng BCD.

Bài 7:

Cho hai số dương x và y thỏa mãn điều kiện x+ y = 7. Tính gần đúng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức sau: Z = (x³ + 2)(y³ + 2)

Bài 8:

Tính gần đúng giá trị của a,b,c,d biết đồ thị của hàm số y = ax³ + bx² + cx + d đi qua bốn điểm

Bài 9:

Trong mặt phẳng tọa độ (Oxy), cho đường thẳng ∆: x - 3y + 7 = 0, parabol và điểm I(4;5). Tìm điểm A thuộc ∆ và điểm B thuộc (P) sao cho I là trung điểm của đoạn thẳng AB, biết B có hoành độ âm.

Bài 10:

Cho hàm số f xác định bởi:

Tìm các giá trị của thỏa mãn phương trình sau: f(2sin²x) + f(3cos²x) = 5f(-5) (*)