Đề thi Olympic môn Toán lớp 9 - Phòng GD Đức Thọ tỉnh Hà Tĩnh

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO ĐỨC THỌ ĐỀ THI CHÍNH THỨC

ĐỀ THI OLYMPIC TOÁN LỚP 9 NĂM HỌC 2012 - 2013 Thời gian làm bài: 120 phút (không kể thời gian giao đề)

Bài 1:

a. Giải phương trình:

b. Với giá trị nào của tham số a thì phương trình sau có nghiệm:

Bài 2:

a. Tìm GTNN của biểu thức:

b. Tìm số thực a để phương trình sau có nghiệm nguyên: x² - ax + a + 2 = 0

Bài 3:

a. Chứng minh rằng đường thẳng (d) có phương trình (m - 3)x - (m - 2)y + m - 1 = 0 (m là tham số) luôn đi qua một điểm cố định A. Tìm tọa độ A

b. Giải hệ phương trình sau: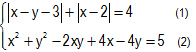

Bài 4:

Cho ΔABC đều cố định nội tiếp trong đường tròn (O). Đường thẳng d thay đổi luôn đi qua A và cắt cung nhỏ AB tại điểm E (E # A). Đường thẳng d cắt hai tiếp tuyên tại B và C của đường tròn (O) lần lượt tại M và N, MC cắt BN tại F. Chứng minh rằng:

a. ΔCAN ~ ΔBMA và ΔMBC ~ ΔBCN

b. Tứ giác BMEF nội tiếp được đường tròn

c. Chứng minh rằng đường thẳng EF luôn đi qua một điểm cố định khi d thay đổi

Bài 5:

Cho a, b, c > 0. Chứng minh rằng: