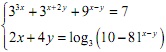Đề thi thử đại học môn Toán năm 2014 tỉnh Thanh Hóa

Đề thi đại học môn Toán khối A

SỞ GIÁO DỤC VÀ ĐÀO TẠO THANH HÓA TRƯỜNG THPT TỐNG DUY TÂN

ĐỀ THI KHẢO SÁT CHẤT LƯỢNG LẦN THỨ NHẤT NĂM HỌC 2013 – 2014 Môn: Toán 12 – Khối A, B, D Thời gian làm bài: 180 phút

I. PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7,0 điểm)

Câu 1 (2,0 điểm): Cho hàm số:

1. Khảo sát sự biến thiên và vẽ đồ thị (C) của đồ thị hàm số (1).

2. Viết phương trình tiếp tuyến của (C) tại điểm M nằm trên (C) có hoành độ lớn hơn 1; biết rằng tiếp tuyến cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B sao cho:

Câu 2 (1,0 điểm). Giải phương trình:

Câu 3 (1,0 điểm). Giải hệ phương trình:

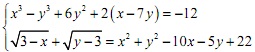
Câu 4 (1,0 điểm). Tính giới hạn:

Câu 5 (1,0 điểm).

Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D; SA vuông góc với mặt đáy (ABCD); AB = 2a; AD = CD = a. Góc giữa mặt phẳng (SBC) và mặt đáy (ABCD) là 60^o. Mặt phẳng (P) đi qua CD và trọng tâm G của tam giác SAB cắt các cạnh SA, SB lần lượt tại M, N. Tính thể tích khối chóp S.CDMN theo a.

Câu 6 (1,0 điểm).

Cho a, b, c là các số dương thỏa mãn 2(a² + b² + c²) = ab + bc + ca + 3. Tìm giá trị lớn nhất của:

II. PHẦN RIÊNG (3,0 điểm): Thí sinh chỉ được làm một trong hai phần riêng (phần A hoặc phần B)

A. Theo chương trình Chuẩn

Câu 7.a (1,0 điểm). Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với A(1; 2), B(3; 4) và đỉnh C nằm trên đường thẳng d: 2x - y + 4 = 0. Viết phương trình đường tròn ngoại tiếp tam giác ABC biết đỉnh C có tung độ dương và diện tích tam giác ABC bằng 2.

Câu 8.a (1,0 điểm). Trong không gian Oxyz, cho hai điểm A(1; 2; -1) và B(-2; 1; 3). Tìm tọa độ điểm C trên trục Ox sao cho tam giác ABC vuông tại C.

Câu 9.a (1,0 điểm). Cho n là số nguyên dương thỏa mãn . Tìm hệ số của x⁷ trong khai triển (1 - 2x³)(2 + x)ⁿ.

B. Theo chương trình Nâng cao

Câu 7.b (1,0 điểm). Trong mặt phẳng tọa độ Oxy, cho elip với hai tiêu điểm F₁, F₂ (hoành độ của F₁ âm). Tìm tọa độ điểm M thuộc elip (E) sao cho góc MF₁F₂ = 60^o.

Câu 8.b (1,0 điểm). Trong không gian Oxyz, cho bốn điểm A(1; 2; 1), B(-2; 1; 3), C(2; -1; 1), D(0; 3; 1). Chứng minh A, B, C, D là bốn đỉnh của một tứ diện. Tính thể tich khối tứ diện đó.

Câu 9.b (1,0 điểm). Giải hệ phương trình: