Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Tĩnh Gia 1, Thanh Hóa

Đề thi thử THPT Quốc gia môn Toán

Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Tĩnh Gia 1, Thanh Hóa là đề thi thử môn Toán có chất lượng, bao gồm đề thi và đáp án thi thử quốc gia 2016 được VnDoc.com sưu tầm và đăng tải. Hi vọng bộ tài liệu này giúp các bạn ôn thi THPT Quốc gia, ôn thi đại học có hiệu quả.

Đề thi thử Quốc gia lần 2 năm 2015 môn Toán trường THPT Tĩnh Gia 1, Thanh Hóa

Đề thi thử Quốc gia môn Toán lần 1 năm 2015 trường Tĩnh Gia 2, Thanh Hóa

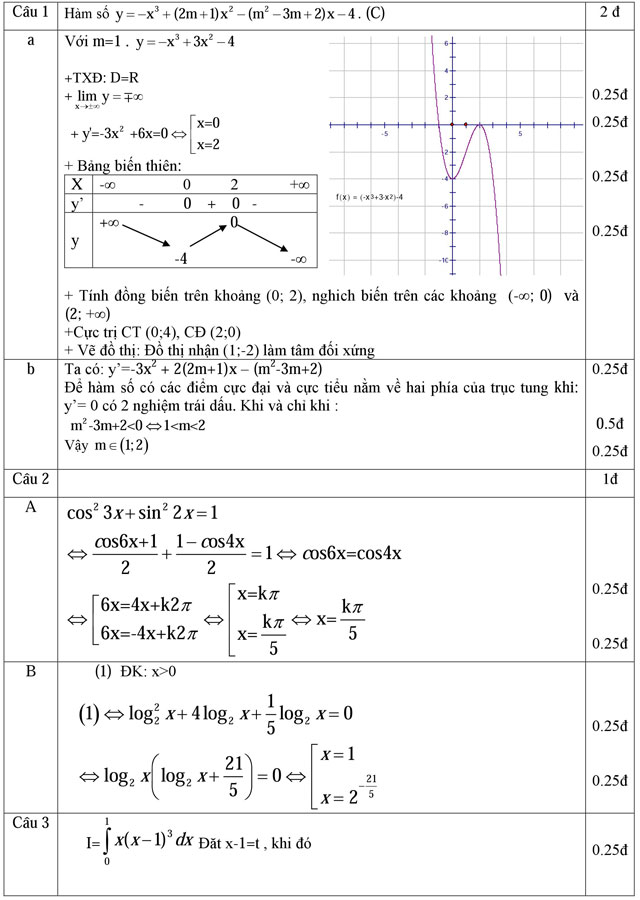
Câu 1 (2 điểm). Cho hàm số y = -x³ + (2m + 1)x² - (m² - 3m + 2)x - 4 (C_m). (Với m là tham số)

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi m = 1 .

b) Tìm m để đồ thị hàm số (C_m) có các điểm cực đại và cực tiểu nằm về hai phía của trục tung.

Câu 2 (1 điểm). Giải các phương trình sau

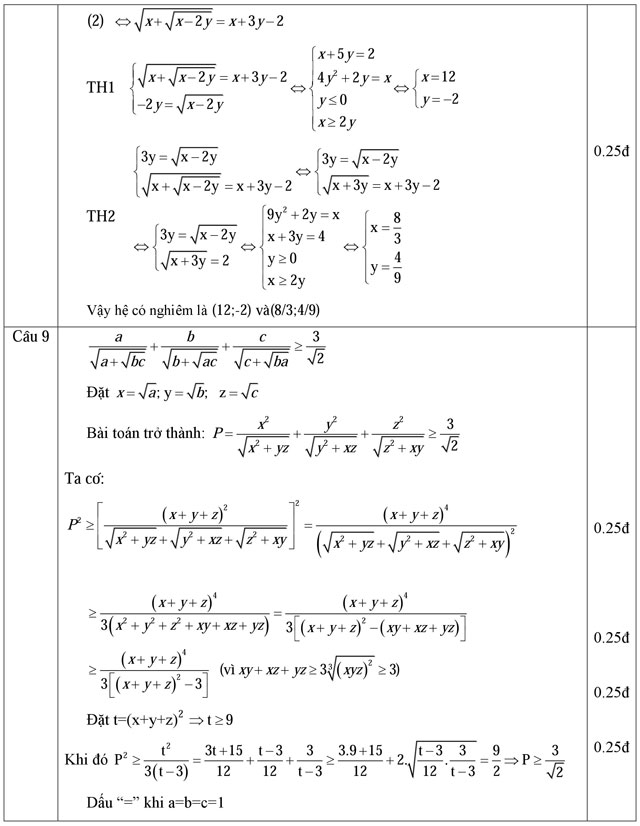
a) cos²3x + sin²2x = 1

Câu 3 (1 điểm). Tính tích phân sau: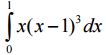

Câu 4 (0.5 điểm).Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn [0; 4]

Câu 5 (0.5 điểm). Cho A là tập hợp các số tự nhiên bé hơn 100, lấy ngẫu nhiên một số từ tập A. Tính xác suất để số lấy được chia hết cho 3.

Câu 6 (1 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc BAD = 60⁰. Các mặt phẳng (SAD) và (SAB) cùng vuông góc với mặt phẳng đáy (ABCD). Góc tạo bởi SC với mp(ABCD) bằng 60⁰. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng NC và SD với N là điểm năm trên cạnh AD sao cho DN = 2AN.

Câu 7 (2 điểm) Trong mặt phẳng tọa độ Oxy

a) Cho điểm M(1; 2), N(3; 1) và đường tròn (C): (x - 1)² + (y - 2)² = 5. Viết phương trình đường thẳng MN và tìm tọa độ giao điểm của đường thẳng MN với đường tròn (C).

b) Cho tam giác cân ABC, (AB = AC). H là trung điểm của BC, D(2;-3) là hình chiếu của H lên AC, M là trung điểm DH và điểm I(16/5; -13/5) là giao điểm của BD với AM. Đường thẳng AC có phương trình: x + y + 1 = 0. Xác định tọa độ các đỉnh của tam giác ABC.

Câu 8 (1 điểm) Giải hệ phương trình:

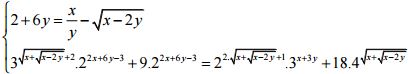
Câu 9 (1 điểm) Cho ba số thực dương a, b, c thoả mãn: abc ≥1. Chứng minh rằng:

Đáp án đề thi thử THPT Quốc gia môn Toán