Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Việt Yên 2, Bắc Giang

Đề thi thử THPT Quốc gia môn Toán

Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Việt Yên 2, Bắc Giang là đề luyện thi thử đại học môn Toán giúp các bạn tự kiểm tra trình độ bản thân, làm thử các đề thi THPT Quốc gia môn Toán các trường, chuẩn bị tốt nhất cho kì thi THPT Quốc gia môn Toán sắp tới.

Đề thi thử THPT Quốc gia môn Toán lần 2 năm 2016 trường THPT Yên Lạc, Vĩnh Phúc

Tuyển tập 20 đề thi thử THPT Quốc gia môn Toán năm 2016

Câu 1. (3,0 điểm)

Cho hàm số (C)

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.

b) Viết phương trình tiếp tuyến với đồ thị (C) tại giao điểm của đồ thị (C) với trục hoành.

c) Tìm m để đường thẳng d: y = 2mx + m + 1 cắt (C) tại hai điểm phân biệt A và B sao cho biểu thức P = OA² + OB² đạt giá trị nhỏ nhất (với O là gốc tọa độ).

Câu 2. (1,0 điểm)

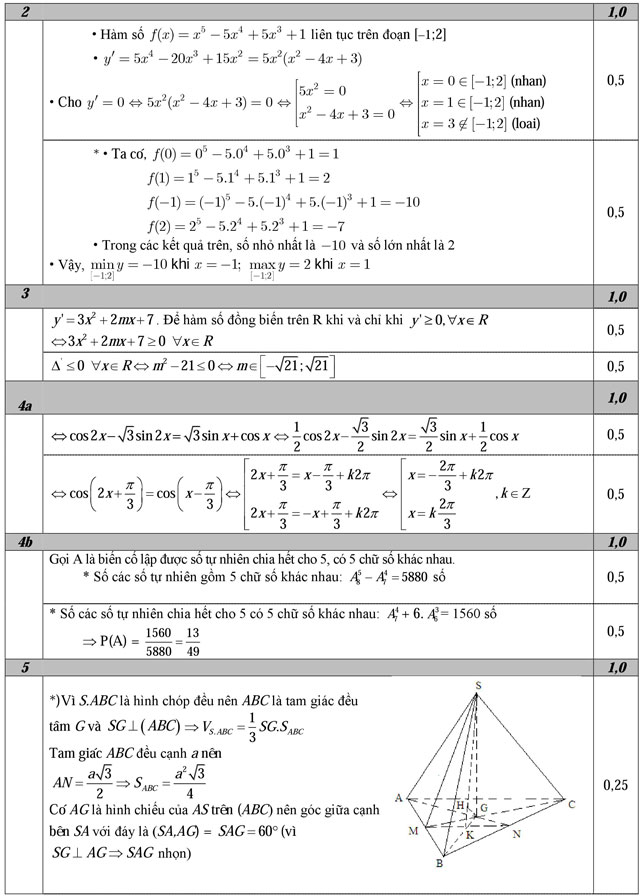
Tìm giá trị lớn nhất và nhỏ nhất của hàm số: f(x) = x⁵ - 5x⁴ + 5x³ + 1 trên đoạn [–1;2]

Câu 3. (1,0 điểm)

Cho hàm số y = x³ + mx² + 7x + 3. Tìm m để hàm số đồng biến trên R.

Câu 4. (2,0 điểm)

a) Giải phương trình cos2x - cosx = √3(sin2x + sinx)

b) Lập số tự nhiên có 5 chữ số khác nhau từ các chữ số {0; 1; 2; 3; 4; 5; 6; 7}. Hãy tính xác suất để lập được số tự nhiên chia hết cho 5.

Câu 5. (1,0 điểm)

Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60⁰. Gọi M, N lần lượt là trung điểm AB, BC. Tính thể tích khối chóp S.ABC và khoảng cách từ C đến mặt phẳng (SMN).

Câu 6. (0,5 điểm)

Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có AB = AD√2, tâm I(1; -2). Gọi M là trung điểm cạnh CD, H(2; -1) là giao điểm của hai đường thẳng AC và BM. Tìm tọa độ các điểm A, B.

Câu 7. (1,0 điểm)

Giải bất phương trình

Câu 8. (0,5 điểm)

Giả sử a, b, c là các số thực dương thỏa mãn a + b + c = 1. Tìm giá trị nhỏ nhất của biểu thức

Đáp án đề thi thử THPT Quốc gia môn Toán