Đề thi thử THPT Quốc gia môn Toán năm 2016 thành phố Cần Thơ

Đề thi thử THPT Quốc gia môn Toán năm 2016

Đề thi thử THPT Quốc gia môn Toán năm 2016 thành phố Cần Thơ là đề thi thử đại học môn Toán có đáp án đi kèm. Đây là tài liệu ôn tập môn Toán hữu ích dành cho các bạn học sinh lớp 12, các bạn thí sinh tự do luyện đề thi thử nhằm chuẩn bị bước vào kì thi THPT Quốc gia, luyện thi Đại học, Cao đẳng 2016. Mời các bạn tham khảo.

Tuyển tập 20 đề thi thử THPT Quốc gia môn Toán năm 2016

Đề thi thử THPT Quốc gia môn Toán năm 2016 tỉnh Hưng Yên

Đề thi thử THPT Quốc gia môn Toán năm 2016 tỉnh Bình Thuận

Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị của hàm số .

Câu 2 (1,0 điểm). Tìm cực trị của hàm số f(x) = x⁴ - 2.

Câu 3 (1,0 điểm).

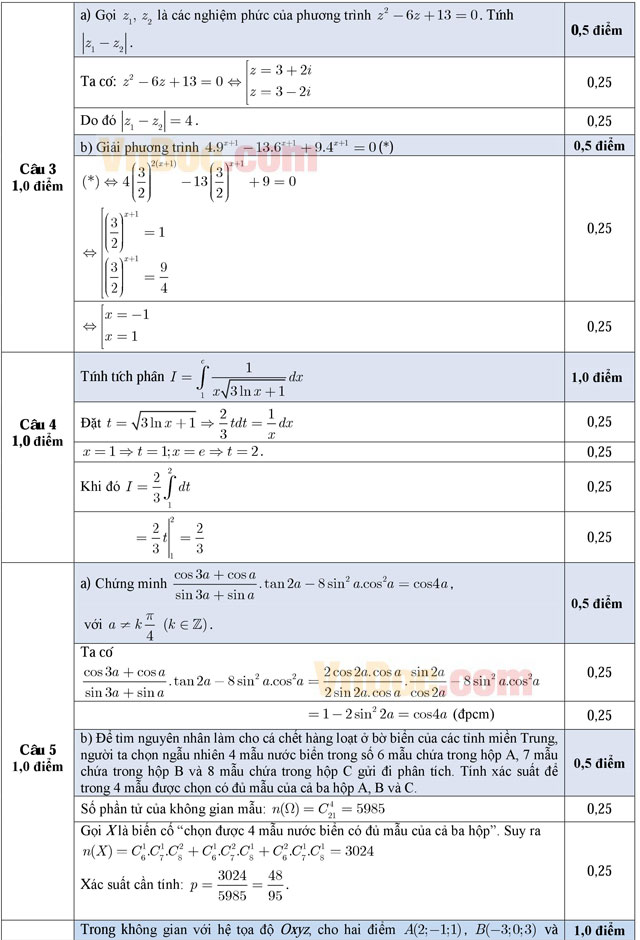
a) Gọi z₁, z₂ là các nghiệm phức của phương trình z² - 6z + 13 = 0. Tính |z₁ - z₂|.

b) Giải phương trình 4.9^x+1 - 13.6^x+1 + 9.4^x+1 = 0.

Câu 4 (1,0 điểm). Tính tích phân .

Câu 5 (1,0 điểm).

a) Chứng minh , với .

b) Để tìm nguyên nhân làm cho cá chết hàng loạt ở bờ biển của các tỉnh miền Trung, người ta chọn ngẫu nhiên 4 mẫu nước biển trong số 6 mẫu chứa trong hộp A, 7 mẫu chứa trong hộp B và 8 mẫu chứa trong hộp C gửi đi phân tích. Tính xác suất để trong 4 mẫu được chọn có đủ mẫu của cả ba hộp A, B và C.

Câu 6 (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;-1;1), B(-3;0;3) và đường thẳng . Viết phương trình mặt phẳng (P) đi qua điểm A và vuông góc với đường thẳng d. Tìm tọa độ điểm M thuộc d sao cho tam giác MAB vuông tại A.

Câu 7 (1,0 điểm). Cho hình lăng trụ ABC.A'B'C' có đáy là một tam giác đều cạnh bằng a, hình chiếu vuông góc của A' trên mặt phẳng (ABC) là trung điểm H của cạnh BC và góc giữa đường thẳng A'A với mặt phẳng (ABC) bằng 60^o. Tính theo a thể tích khối lăng trụ ABC.A'B'C' và khoảng cách từ điểm B đến mặt phẳng (ACC'A').

Câu 8 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC nội tiếp trong đường tròn (T) có phương trình 4x² + 4y² - 58x - 5y + 54 = 0. Trên cạnh AB lấy điểm M (M khác với A, B) và trên cạnh AC lấy điểm N (N khác với A, C) sao cho BM = CN. Gọi D, E theo thứ tự là trung điểm của BC và MN. Đường thẳng DE cắt các đường thẳng AB, AC theo thứ tự tại P, Q. Tìm tọa độ các điểm A, B, C biết là tung độ của A là một số nguyên.

Câu 9 (1,0 điểm).

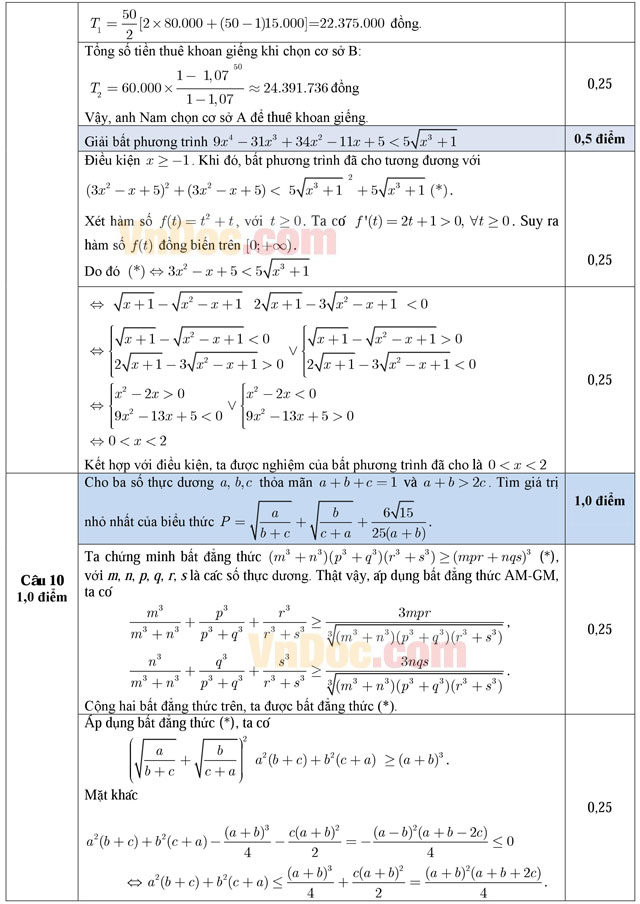
a) Do nắng nóng kéo dài và nước biển xâm nhập nên người dân của một số tỉnh miền Tây thiếu nước ngọt sinh hoạt trầm trọng, trong đó có gia đình anh Nam. Vì vậy, anh Nam thuê khoan một giếng sâu 50 mét để lấy nước sinh hoạt và được hai cơ sở khoan giếng báo giá như sau: Cơ sở A, giá của mét khoan đầu tiên là 80.000 đồng và kể từ mét khoan thứ hai, giá của mỗi mét khoan sau tăng thêm 15.000 đồng so với giá của mét khoan ngay trước đó; cơ sở B, giá của mét khoan đầu tiên là 60.000 đồng và kể từ mét khoan thứ hai, giá của mỗi mét khoan sau tăng thêm 7% so với giá của mét khoan ngay trước đó. Anh Nam chọn cơ sở nào để thuê khoan giếng sao cho tiền thuê là thấp nhất?

b) Giải bất phương trình

Câu 10 (1,0 điểm). Cho ba số thực dương a, b, c thỏa mãn a + b + c = 1 và a + b > 2c. Tìm giá trị nhỏ nhất của biểu thức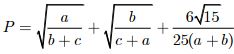

Đáp án đề thi thử THPT Quốc gia môn Toán năm 2016