Đề thi thử THPT Quốc gia môn Toán năm 2016 tỉnh Bình Thuận
Đề thi thử THPT Quốc gia môn Toán năm 2016
Đề thi thử THPT Quốc gia môn Toán năm 2016 tỉnh Bình Thuận được VnDoc.com sưu tầm và đăng tải. Hi vọng tài liệu này sẽ giúp các em học sinh lớp 12, các bạn thí sinh tự do có thêm đề luyện tập, ôn thi đại học môn Toán, ôn thi THPT Quốc gia môn Toán. Mời các bạn cùng tham khảo.
Đề thi thử THPT Quốc gia môn Hóa học năm 2016 tỉnh Bình Thuận
Đề thi thử THPT Quốc gia môn Ngữ văn năm 2016 tỉnh Bình Thuận
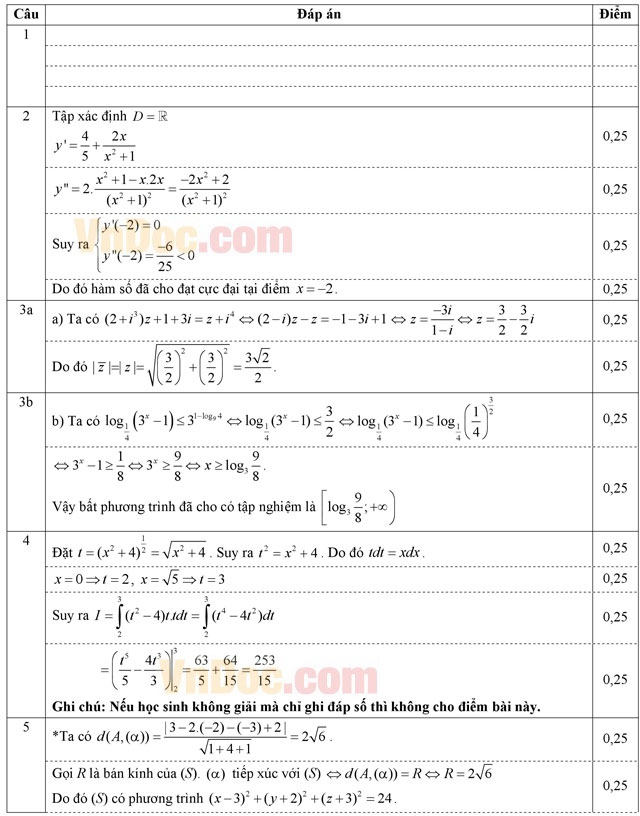
| SỞ GIÁO DỤC VÀ ĐÀO TẠO BÌNH THUẬN ĐỀ CHÍNH THỨC | KỲ THI THỬ TRUNG HỌC PHỔ THÔNG QUỐC GIA NĂM 2016 Môn thi: TOÁN Thời gian làm bài: 180 phút, không kể thời gian phát đề |
Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị của hàm số 
.
Câu 2 (1,0 điểm). Chứng minh hàm số 
đạt cực đại tại điểm x = -2.
Câu 3 (1,0 điểm).
a) Tìm môđun của số phức 
biết (2 + i3)z + 1 + 3i = z + i4.
b) Giải bất phương trình 
.
Câu 4 (1,0 điểm). Tính tích phân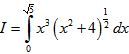 
.
Câu 5 (1,0 điểm). Trong không gian Oxyz cho mặt phẳng (α): x - 2y - z + 2 = 0 và điểm A(3; -2; -3). Viết phương trình mặt cầu (S) tâm A và tiếp xúc với mặt phẳng (α). Tìm tọa độ tiếp điểm của (S) và (α).
Câu 6 (1,0 điểm).
a) Cho sinα = 5/13 với π/2 < α < π. Tính giá trị của 
.
b) Một chiếc tàu của tập đoàn dầu khí quốc gia Việt Nam khoan thăm dò dầu khí trên thềm lục địa tỉnh Bình Thuận có xác suất khoan trúng túi dầu là p. Tìm p biết rằng trong hai lần khoan độc lập, xác suất để chiếc tàu đó khoan trúng túi dầu ít nhất một lần là 0,36.
Câu 7 (1,0 điểm). Cho lăng trụ tam giác ABC.A'B'C' có đáy ABC là tam giác đều cạnh a; góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 60o; A'A = A'B = A'C. Tính theo a thể tích của khối lăng trụ ABC.A'B'C' và khoảng cách giữa hai đường thẳng AA' và B'C'.
Câu 8 (1,0 điểm). Trong mặt phẳng Oxy cho đường tròn (I) có hai đường kính AB và MN với A(2; -1), B(2; -5). Gọi E và F lần lượt là giao điểm của các đường thẳng AM và AN với tiếp tuyến của (I) tại B. Tìm tọa độ trực tâm H của tam giác MEF sao cho H nằm trên đường thẳng Δ: x - 2y - 2 = 0 và có hoành độ là một số nguyên.
Câu 9 (1,0 điểm). Giải phương trình 
trên tập hợp số thực.
Câu 10 (1,0 điểm). Cho a, b, c là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức
Đáp án đề thi thử THPT Quốc gia môn Toán năm 2016
