Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Nguyễn Thị Minh Khai, Hà Tĩnh (Lần 3)
Đề thi thử THPT Quốc gia năm 2016 môn Toán
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Nguyễn Thị Minh Khai, Hà Tĩnh (Lần 3) là một trong các đề thi thử đại học môn Toán mà VnDoc lần này gửi tới các bạn. Đây là tài liệu tham khảo hay dành cho các bạn học sinh luyện thi đại học môn Toán, ôn thi THPT Quốc gia môn Toán hiệu quả.
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Minh Châu, Hưng Yên (Lần 2)
| SỞ GD & ĐT HÀ TĨNH TRƯỜNG THPT N.T.MINH KHAI |
ĐỀ THI THỬ THPT QUỐC GIA LẦN 3 NĂM HỌC: 2015 - 2016 Môn: TOÁN - Lớp 12 Thời gian: 180 phút (không kể thời gian giao đề) |
Câu 1. (1,0 điểm) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số y = x4 - 2x2 - 1.
Câu 2. (1,0 điểm) Cho hàm số: y = x3 + 3x2 - 9x + 5. Viết phương trình tiếp tuyến của hàm số biết hệ số tiếp tuyến y' min.
Câu 3. (1,0 điểm)
a) Giải phương trình: log3(x + 1) + log3(3 - x) = log3(2x + 3).
b) Giải phương trình: cos3x + sin3x = 1 - 2cos2x.
Câu 4. (1,0 điểm) Tính tích phân: ![]()
Câu 5. (1,0 điểm) Trong không gian với hệ tọa độ Oxyz cho ba điểm A(1;-2;1), B(-1;0;3), C(0;2;1). Lập phương trình mặt cầu tâm C, đường kính AB và tìm tọa độ điểm H là chân đường cao kẻ từ A của tam giác ABC.
Câu 6. (1,0 điểm)
a) Cho số phức z = 1 + 3i. Tìm số nghịch đảo của số phức: ![]()
b) Tìm số hạng không chứa x trong khai triển: ![]() với x > 0.
với x > 0.
Câu 7. (1,0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy, góc giữa cạnh bên SC và đáy bằng 60o. Tính theo a thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng BD và SA.
Câu 8. (1,0 điểm) Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có tọa độ các đỉnh A(2;3), B(2;1), C(6;3). Gọi D là chân đường phân giác trong góc A của tam giác ABC. Tìm điểm M trên đường tròn (C): (x - 3)2 + (y - 1)2 = 25 sao cho diện tích tam giác MDC gấp đôi diện tích tam giác ABD.
Câu 9. (1,0 điểm) Giải hệ phương trình sau:
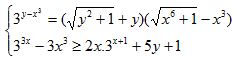
Câu 10. (1,0 điểm) Cho a, b, c là các số thực (a, b, c ≥ 1) thỏa mãn: 2abc + 1 ≥ a + b + c. Tìm giá trị lớn nhất của biểu thức:
![]()
- HẾT -


