Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Bắc Yên Thành, Nghệ An

Đề thi thử THPT Quốc gia năm 2016 môn Toán

Nhằm giúp các bạn học sinh có thêm nhiều đề thi thử để luyện tập, củng cố lại kiến thức, VnDoc.com xin giới thiệu tới các bạn Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Bắc Yên Thành, Nghệ An. Hi vọng tài liệu này giúp các bạn ôn thi đại học môn Toán, luyện thi THPT Quốc gia môn Toán hiệu quả hơn.

Đề thi thử THPT Quốc gia năm 2016 môn Vật lý trường THPT Bắc Yên Thành, Nghệ An

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Minh Châu, Hưng Yên (Lần 2)

Trường THPT Bắc Yên Thành LỚP 12A4 Ngày 05/4/2016

ĐỀ KIỂM TRA NĂNG LỰC THI THPT QUỐC GIA NĂM 2016 Môn thi: TOÁN Thời gian làm bài: 180 phút, không kể thời gian giao đề

Câu 1 (2,0 điểm) Cho hàm số .

a. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.

b. Tìm m để đường thẳng (d): y = 2x + m cắt (C) tại hai điểm phân biệt và tiếp tuyến của (C) tại hai điểm đó song song với nhau.

Câu 2 (2,0 điểm)

a. Giải phương trình sinx(cos4x + 2) = sin²2x - 3/2.

b. Giải phương trình x³ + x + 2(x² + 1)√x = 6.

Câu 3 (2,0 điểm)

a. Tính tích phân .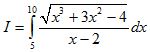

b. Gọi z₁ và z₂ là hai nghiệm phức của phương trình 2(1 + i)z² - 4(2 - i)z - 5 - 3i = 0.

Tính |z₁|² + |z₂|².

Câu 4 (1,0 điểm) Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, với AC = a/2, BC = a. Hai mặt phẳng (SAB) và (SAC) cùng tạo với mặt đáy (ABC) góc 60⁰. Tính theo a thể tích khối chóp S.ABC và khoảng cách từ điểm B tới mặt phẳng (SAC), biết rằng mặt phẳng (SBC) vuông góc với đáy (ABC).

Câu 5 (2,0 điểm)

a. Trong mặt phẳng tọa độ Oxy cho tam giác ABC vuông cân tại A. Biết phương trình cạnh BC là (d): x + 7y - 31 = 0, điểm N(7; 7) thuộc đường thẳng AC, điểm M(2; -3) thuộc AB và nằm ngoài đoạn AB. Tìm tọa độ các đỉnh của tam giác ABC.

b. Trong không gian với hệ tọa độ cho mặt phẳng (P): x + 2y - z + 5 = 0 và đường thẳng . Gọi d' là hình chiếu vuông góc của d lên (P) và E là giao điểm của d và (P). Viết phương trình đường thẳng d'. Tìm tọa độ điểm F thuộc (P) sao cho EF vuông góc với d' và EF = 5√3.

Câu 6 (1,0 điểm) Cho các số thực a, b, c không âm thỏa mãn a² + b² + c² = 1. Chứng minh rằng

Đáp án đề thi thử THPT Quốc gia năm 2016 môn Toán