Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Minh Châu, Hưng Yên (Lần 2)

Đề thi thử THPT Quốc gia năm 2016 môn Toán

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Minh Châu, Hưng Yên (Lần 2) gồm 10 câu hỏi có đáp án đi kèm, là đề luyện thi THPT Quốc gia hữu ích dành cho các bạn học sinh lớp 12, những bạn chuẩn bị bước vào kì thi THPT Quốc gia, luyện thi Đại học, Cao đẳng 2016. Mời các bạn tham khảo.

Tổng hợp hơn 230 đề thi thử THPT Quốc gia môn Toán năm 2016 các trường THPT trên toàn quốc

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường Đại học Hồng Đức, Thanh Hóa

Đề thi thử THPT Quốc gia môn Toán năm 2016 tỉnh Hà Nam

TRƯỜNG THPT MINH CHÂU Tổ: TỰ NHIÊN ĐỀ CHÍNH THỨC

ĐỀ THI THỬ LẦN II - KỲ THI THPT QUỐC GIA NĂM 2016 Môn: TOÁN Thời gian làm bài: 180 phút, không kể thời gian phát đề Ngày thi: 27/02/2016

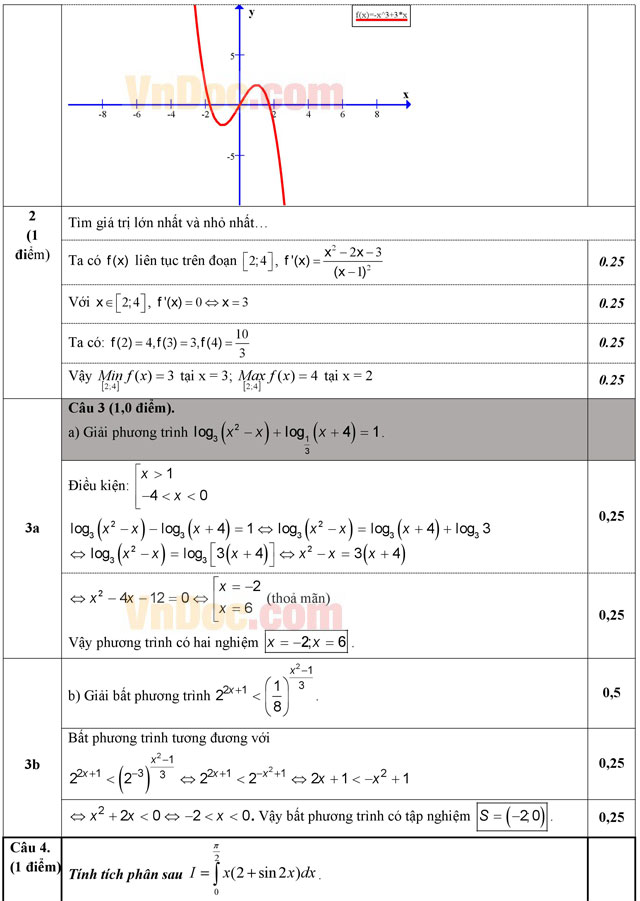
Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị (C) hàm số y = -x³ + 3x.

Câu 2 (1,0 điểm). Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [2; 4].

Câu 3 (1,0 điểm).

a) Giải phương trình: .

b) Giải bất phương trình .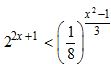

Câu 4 (1,0 điểm) Tính tích phân sau .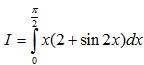

Câu 5: (1,0 điểm) Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(2;1;-3), B(4;3;-2), C(6;-4;-1). Chứng minh rằng A, B,C là ba đỉnh của một tam giác vuông và viết phương trình mặt cầu tâm A đi qua trọng tâm G của tam giác ABC.

Câu 6 (1,0 điểm)

a) Cho góc α thoả mãn 3π/2 < α < 2π và cosα = 4/5. Tính giá trị biểu thức .

b) Đội văn nghệ của nhà trường gồm 4 học sinh lớp 12A, 3 học sinh lớp 12B và 2 học sinh lớp 12C. Chọn ngẫu nhiên 5 học sinh từ đội văn nghệ để biểu diễn trong lễ bế giảng năm học. Tính xác suất sao cho lớp nào cũng có học sinh được chọn và có ít nhất 2 học sinh lớp 12A.

Câu 7 (1,0 điểm). Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SD = 3a/2. Hình chiếu vuông góc H của đỉnh S lên mặt phẳng (ABCD) là trung điểm của đoạn AB. Gọi K là trung điểm của đoạn AD. Tính theo a thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng HK và SD.

Câu 8 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC vuông tại A nội tiếp đường tròn (T) có phương trình: x² + y² - 6x - 2y + 5 = 0. Gọi H là hình chiếu của A trên BC. Đường tròn đường kính AH cắt AB, AC lần lượt tại M, N. Tìm tọa độ điểm A và viết phương trình cạnh BC, biết đường thẳng MN có phương trình: 20x - 10y - 9 = 0 và điểm H có hoành độ nhỏ hơn tung độ.

Câu 9 (1,0 điểm) Giải hệ phương trình: .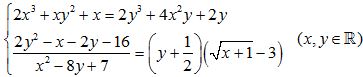

Câu 10 (1,0 điểm) Cho a, b, c là các số thực dương thoả mãn a + b + c = 3. Tìm giá trị lớn nhất của biểu thức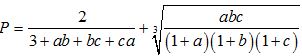

Đáp án đề thi thử THPT Quốc gia năm 2016 môn Toán