Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Hồng Quang, Hải Dương (Lần 3)
Đề thi thử THPT Quốc gia năm 2016 môn Toán
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Hồng Quang, Hải Dương (Lần 3) là đề thi thử đại học môn Toán có đáp án đi kèm được VnDoc.com sưu tầm và đăng tải. Đây là tài liệu ôn thi THPT Quốc gia, luyện thi Đại học, Cao đẳng môn Toán hữu ích dành cho các bạn thí sinh chuẩn bị bước vào kì thi quan trọng này.
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Hồng Quang, Hải Dương (Lần 1)
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Hồng Quang, Hải Dương (Lần 2)
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Hồng Quang, Hải Dương (Lần 4)
|
SỞ GD & ĐT HẢI DƯƠNG TRƯỜNG THPT HỒNG QUANG |
ĐỀ THI THỬ LẦN 3 KÌ THI THPT QUỐC GIA NĂM 2016 MÔN: TOÁN (Thời gian làm bài: 180 phút, không kể thời gian phát đề). |
Câu 1 (2,0 điểm)
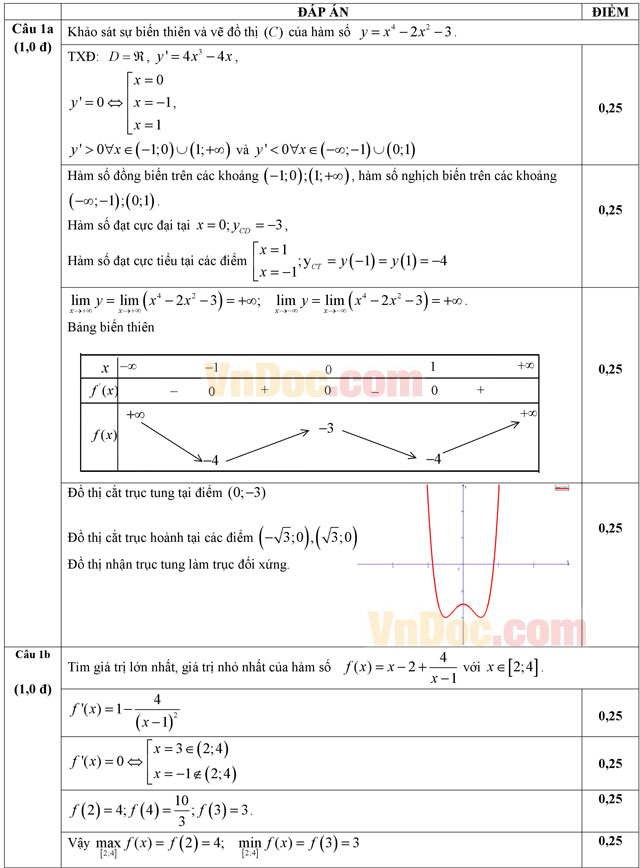
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số y = x4 - 2x2 - 3.
b) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 
với x ∈ [2; 4].
Câu 2 (1,0 điểm)
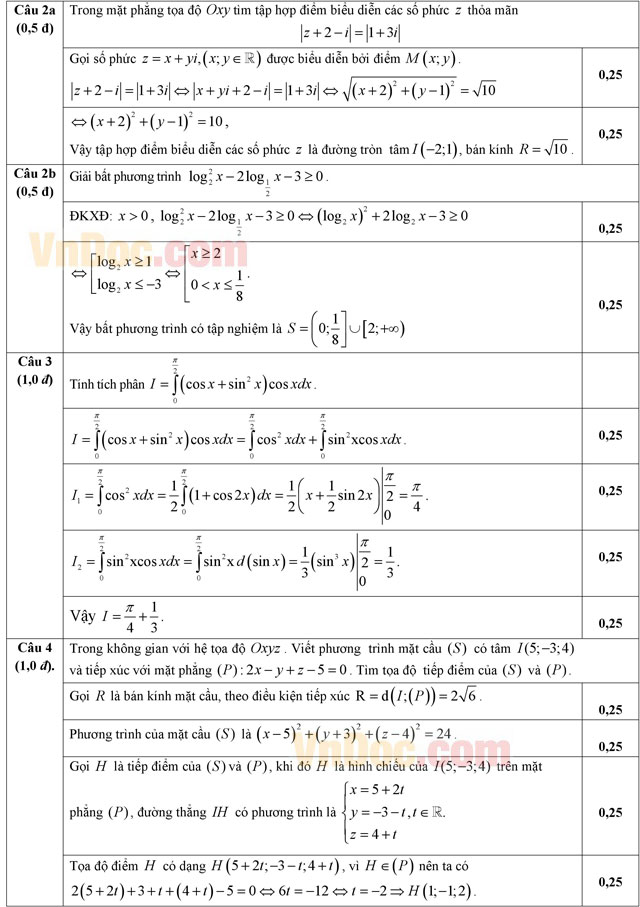
a) Trong mặt phẳng tọa độ Oxy tìm tập hợp điểm biểu diễn các số phức z thỏa mãn |z + 2 - i| = |1 + 3i|.
b) Giải bất phương trình 
.
Câu 3 (1,0 điểm) Tính tích phân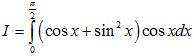 
.
Câu 4 (1,0 điểm) Trong không gian với hệ tọa độ Oxyz. Viết phương trình mặt cầu (S) có tâm I(5; -3; 4) và tiếp xúc với mặt phẳng (P): 2x - y + z - 5 = 0. Tìm tọa độ tiếp điểm của (S) và (P).
Câu 5 (1,0 điểm)
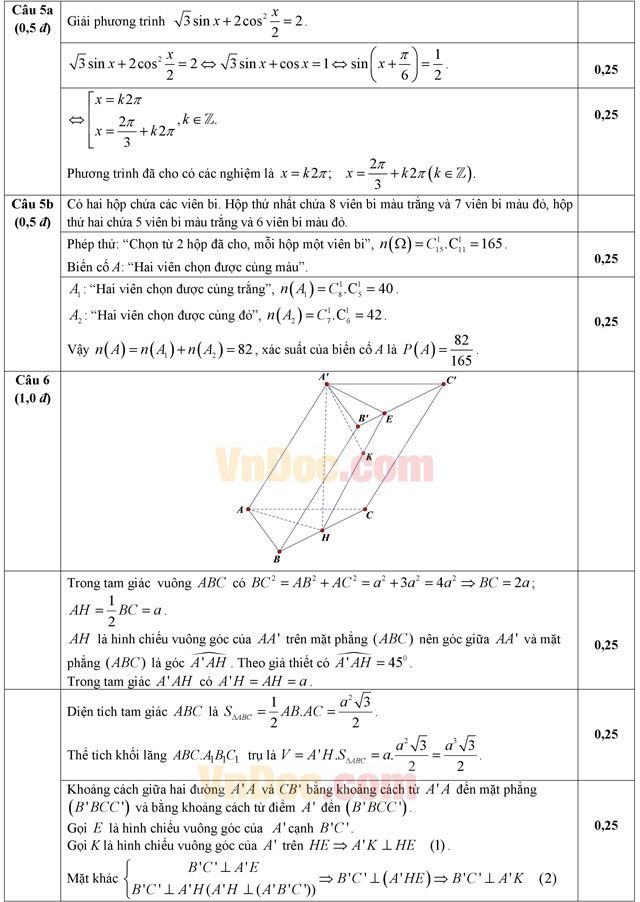
a) Giải phương trình 
.
b) Có hai hộp chứa các viên bi. Hộp thứ nhất chứa 8 viên bi màu trắng và 7 viên bi màu đỏ, hộp thứ hai chứa 5 viên bi màu trắng và 6 viên bi màu đỏ. Từ mỗi hộp lấy ngẫu nhiên một viên bi. Tính xác xuất sao cho hai viên bi lấy ra cùng màu.
Câu 6 (1,0 điểm). Cho lăng trụ tam giác ABC.A'B'C' có đáy là tam giác vuông tại A, AB = a, AC = a√3. Hình chiếu vuông góc của A' trên mặt phẳng (ABC) trùng với trung điểm H của cạnh BC. Góc giữa cạnh bên và mặt đáy bằng 45o. Tính theo a thể tích khối lăng trụ ABC.A'B'C' và khoảng cách giữa hai đường thẳng AA', CB'.
Câu 7 (1,0 điểm). Trong mặt phẳng tọa độ Oxy, cho hình thang vuông ABCD, vuông tại A và B, có đỉnh C(0; 2) và AD = 3BC. Gọi H là hình chiếu vuông góc của A trên đường chéo BD. Điểm 
là điểm thuộc đoạn HD sao cho 2HM = MD. Tìm tọa độ các đỉnh A, B, D của hình thang vuông ABCD biết đỉnh A thuộc đường thẳng (d): x - y - 1 = 0.
Câu 8 (1,0 điểm). Giải hệ phương trình: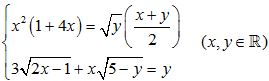 
.
Câu 9 (1,0 điểm). Cho các số dương a, b, c thỏa mãn a + b + 1 = c. Tìm giá trị nhỏ nhất của biểu thức
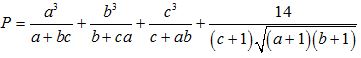
Đáp án đề thi thử THPT Quốc gia năm 2016 môn Toán
