Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Nam Duyên Hà, Thái Bình (Lần 2)

Đề thi thử THPT Quốc gia môn Toán năm 2016

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Nam Duyên Hà, Thái Bình (Lần 2) được VnDoc.com sưu tầm và đăng tải, là tài liệu tham khảo hữu ích dành cho các bạn thí sinh chuẩn bị bước vào kì thi THPT Quốc gia 2016 sắp tới. Mời các bạn tham khảo.

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Xuân Trường, Nam Định (Lần 2)

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Nam Duyên Hà, Thái Bình (Lần 1)

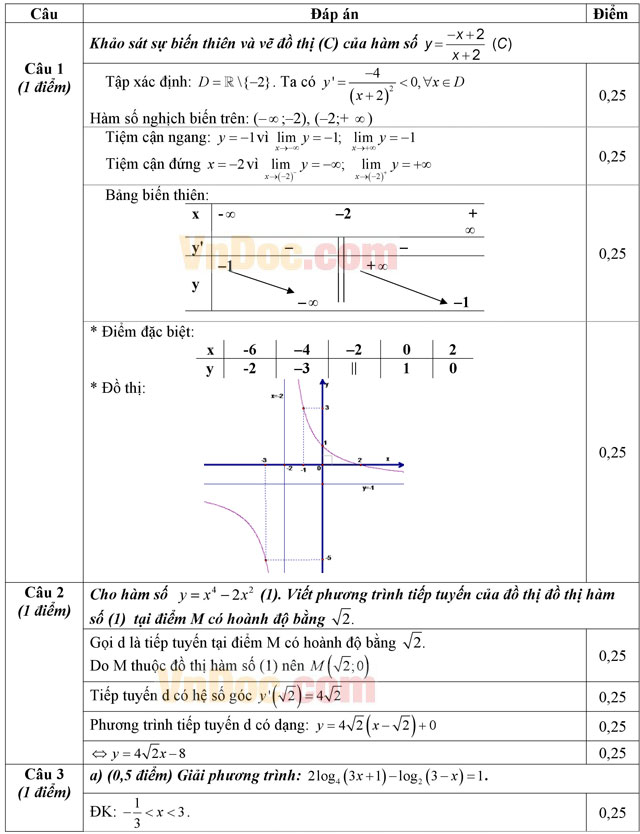
Câu 1. (1,0 điểm) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (C).

Câu 2. (1,0 điểm) Cho hàm số y = x⁴ - 2x² (1). Viết phương trình tiếp tuyến của đồ thị đồ thị hàm số (1) tại điểm M có hoành độ bằng √2.

Câu 3. (1,0 điểm)

a) Giải phương trình: 2log₄(3x + 1) - log₂(3 - x) = 1.
b) Cho số phức z = 3 - 2i. Tìm phần thực và phần ảo của số phức .

Câu 4. (1,0 điểm)

a) Giải phương trình: sin2x + 4 = 8cosx + sinx.

b) Trong một đợt phỏng vấn học sinh trường THPT Nam Duyên Hà để chọn 6 học sinh đi du học Nhật Bản với học bổng là được hỗ trợ 80% kinh phí đào tạo. Biết số học sinh đi phỏng vấn gồm 5 học sinh lớp 12A2, 7 học sinh lớp 12A3, 8 học sinh lớp 12A4 và 10 học sinh lớp 12A5. Giả sử cơ hội của các học sinh vượt qua cuộc phỏng vấn là như nhau. Tính xác suất để có ít nhất 2 học sinh lớp 12A2 được chọn.

Câu 5. (1,0 điểm) Tính tích phân: .

Câu 6. (1,0 điểm) Trong không gian cho hình chóp S.ABCD có đáy là tam giác vuông tại B, BC = 3a, AC = a√10, cạnh bên SA vuông góc với đáy, góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) bằng 60^o. Tính thể tích khối chóp S.ABC và khoảng cách giữa hai đường thẳng SM và AC theo a, biết M là điểm trên đoạn BC sao cho MC = 2BM.

Câu 7. (1.0 điểm) Trong không gian với hệ tọa độ Oxyz cho hai điểm A(1; -1; 2) và B(3; 0; 4) mặt phẳng (P): x - 2y + 2z - 5 = 0. Viết phương trình tham số của đường thẳng AB, tìm tọa độ giao điểm của đường thẳng AB và mặt phẳng (P), viết phương trình mặt phẳng chứa đường thẳng AB và vuông góc với mặt phẳng (P).

Câu 8. (1,0 điểm) Giải hệ phương trình: .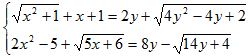

Câu 9. (1,0 điểm) Trong mặt phẳng Oxy, cho tam giác ABC có tâm đường tròn ngoại tiếp I(-2; 1) và thỏa mãn điều kiện góc AIB = 90^o. Chân đường cao kẻ từ A đến BC là D(-1; -1). Đường thẳng AC qua M(-1; 4). Tìm tọa độ các đỉnh A, B biết đỉnh A có hoành độ dương.

Câu 10. (1.0 điểm) Cho các số thực không âm a, b, c thoả mãn a² + b² + c² - 3b ≤ 0. Tìm giá trị nhỏ nhất của biểu thức sau:

Đáp án đề thi thử THPT Quốc gia môn Toán năm 2016