Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Yên Lạc 2, Vĩnh Phúc (Lần 4)
Đề thi thử THPT Quốc gia môn Toán năm 2016
Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Yên Lạc 2, Vĩnh Phúc (Lần 4) có đáp án được VnDoc.com sưu tầm và đăng tải, giúp các bạn ôn tập THPT Quốc gia môn Toán, luyện thi đại học môn Toán hiệu quả. Mời các bạn tham khảo.
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Vĩnh Phúc (Lần 5)
Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Ân Thi, Hưng Yên (Lần 3)
| TRƯỜNG THPT YÊN LẠC 2 | ĐỀ THI KHẢO SÁT CHẤT LƯỢNG LẦN 4 NĂM HỌC 2015 - 2016 Môn: TOÁN, Khối: 12 Thời gian làm bài: 180 phút, không kể thời gian phát đề |
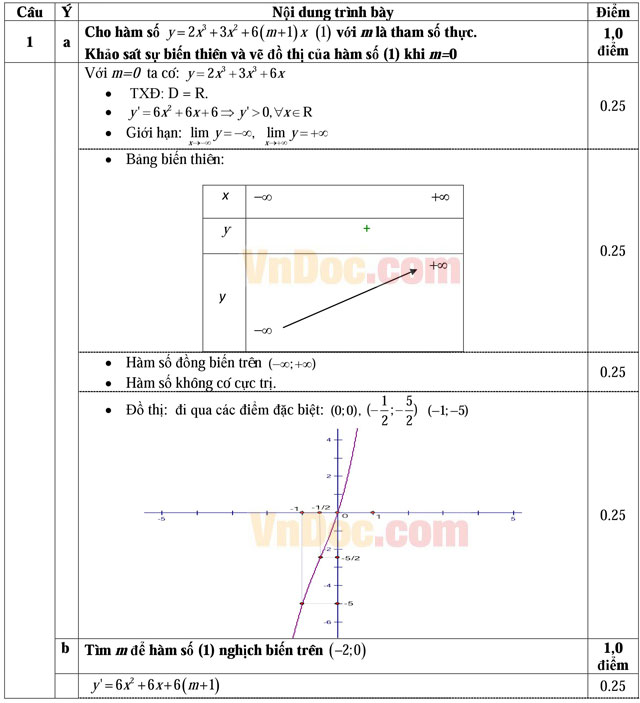
Câu 1 (02 điểm): Cho hàm số y = 2x3 + 3x2 + 6(m + 1)x (1) với m là tham số thực.
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi m = 0.
b) Tìm m để hàm số (1) nghịch biến trên (-2; 0).
Câu 2 (01 điểm):
a) Giải phương trình 
.
b) Cho số phức z thỏa mãn 
. Tìm mô đun của số phức w = z + 1 + i.
Câu 3 (01 điểm): Tính diện tích hình phẳng được giới hạn bởi các đường sau y = xlnx, y = 0, x = 1, x = e.
Câu 4 (01 điểm):
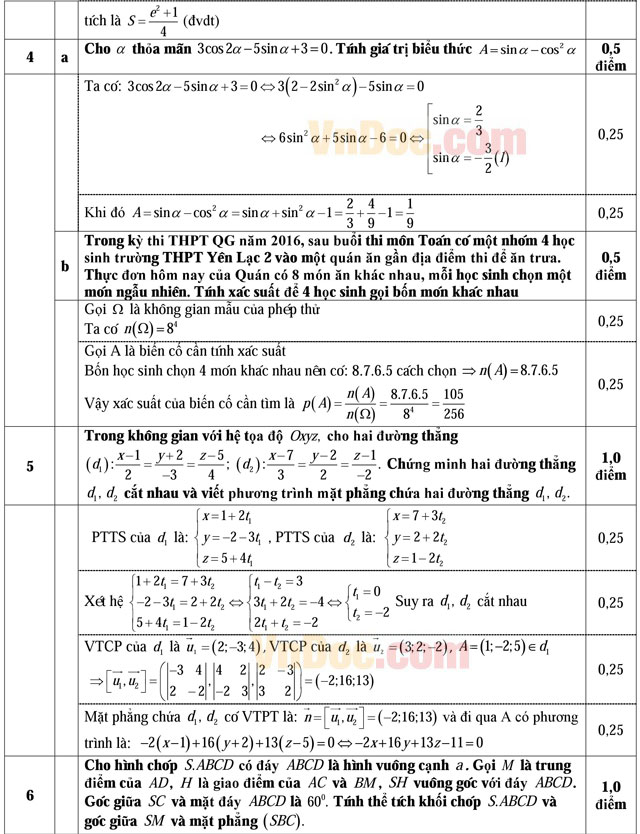
a) Cho α thỏa mãn 3cos2α - 5sinα + 3 = 0. Tính giá trị biểu thức A = sinα - cos2α.
b) Trong kỳ thi THPT QG năm 2016, sau buổi thi môn Toán có một nhóm 4 học sinh trường THPT Yên Lạc 2 vào một quán ăn gần địa điểm thi để ăn trưa. Thực đơn hôm nay của Quán có 8 món ăn khác nhau, mỗi học sinh chọn một món ngẫu nhiên. Tính xác suất để 4 học sinh gọi bốn món khác nhau.
Câu 5 (01 điểm): Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng 
; 
. Chứng minh hai đường thẳng d1, d2 cắt nhau và viết phương trình mặt phẳng chứa hai đường thẳng d1, d2.
Câu 6 (01 điểm): Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M là trung điểm của AD, H là giao điểm của AC và BM, SH vuông góc với đáy ABCD. Góc giữa SC và mặt đáy ABCD là 600. Tính thể tích khối chóp S.ABCD và góc giữa SM và mặt phẳng (SBC).
Câu 7 (01 điểm): Trong mặt phẳng với hệ trục tọa độ Oxy, cho tam giác nhọn ABC. Gọi M(-1; -2), N(2; 2), P(-1; 2) theo thứ tự là chân đường cao hạ từ các đỉnh A, B, C. Viết phương trình đường thẳng chứa cạnh AC.
Câu 8 (01 điểm): Giải hệ phương trình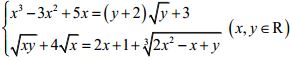 
Câu 9 (01 điểm): Cho ba số thực không âm x, y, z. Tìm giá trị lớn nhất của biểu thức:
Đáp án đề thi thử THPT Quốc gia môn Toán năm 2016
