Giải Lý 10 Bài 21: Động học học của chuyển động tròn. Lực hướng tâm CTST
Giải Lý 10 Bài 21 CTST
Giải Lý 10 Bài 21: Động học học của chuyển động tròn. Lực hướng tâm CTST được VnDoc.com sưu tầm và xin gửi tới bạn đọc cùng tham khảo.
Mở đầu trang 131 SGK Lý 10 CTST
Em nhận xét gì về mặt đường đua trong Hình 21.1? Tại sao người ta phải xây dựng mặt đường ở một số đoạn vòng cung có độ nghiêng so với phương ngang như vậy?
Lời giải:
Mặt đường trơn trượt, lực ma sát giữa các bánh xe và mặt đường không đủ để tạo lực hướng tâm. Do đó để xe không bị văng ra ngoài, mặt đường phải thiết kế nghiêng một góc so với phương ngang, đảm bảo cho xe chạy theo quỹ đạo tròn.
1. Lực hướng tâm
Khái niệm lực hướng tâm
Câu hỏi 1 trang 132 SGK Lý 10 CTST
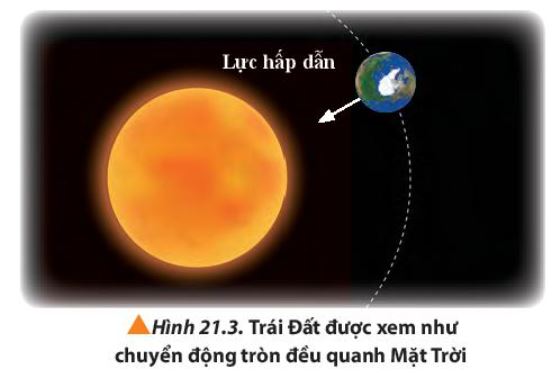
Trong hệ Mặt Trời, chuyển động của một số hành tinh như Trái Đất được xem gần đúng là chuyển động tròn đều xung quay Mặt Trời (Hình 21.3). Lực nào đóng vai trò là lực hướng tâm trong chuyển động này của Trái Đất?
Lời giải:
Lực đóng vai trò là lực hướng tâm trong chuyển động của Trái Đất quanh Mặt Trời là lực hấp dẫn.
Luyện tập trang 132 SGK Lý 10 CTST
Vinasat – 1 là vệ tinh viễn thông địa tĩnh (có vị trí cố định trong không gian so với Trái Đất) đầu tiên của Việt Nam được phóng vào vũ trụ năm 2008. Biết khối lượng vệ tinh là m = 2,7 tấn và vệ tinh có quỹ đạo chuyển động nằm trong mặt phẳng xích đạo cách tâm Trái Đất 42000 km. Hãy xác định độ lớn lực hướng tâm do Trái Đất tác dụng lên vệ tinh.
Lời giải:
Đổi đơn vị: 2,7 tấn = 2,7.103 kg; 42000 km = 42.106 m.
Chu kì của Trái Đất: T = 84600 s.
Độ lớn lực hướng tâm do Trái Đất tác dụng lên vệ tinh là:
Fht = m.ω2.R = m.
\(\left ( \frac{2\pi }{T} \right )^{2}\).R = 2,7.103.\(\left ( \frac{2\pi }{254600} \right ) ^{2}\).42.106 = 599,7 N
2. Ứng dụng trong thực tế của chuyển động tròn
Trường hợp xe chạy theo đường vòng cung trên mặt đường ngang
Câu hỏi 2 trang 132 SGK Lý 10 CTST
Khi ô tô chạy theo đường vòng cung, tài xế cần lưu ý những điều gì để tránh xảy ra tai nạn?
Lời giải:
Khi chạy theo đường vòng cung, tài xế cần lưu ý đảm bảo tốc độ để duy trì được vị trí của xe. Nếu chạy với tốc độ quá chậm, xe sẽ có xu hướng trược xuống phía tâm đường cong. Nếu chạy quá nhanh, xe có xu hướng bị văng ra ngoài đường cong.
Luyện tập trang 133 SGK Lý 10 CTST
Cho bán kính cung tròn mà xe chạy theo bằng 35,0 m, hệ số ma sát nghỉ giữa mặt đường và bánh xe bằng 0,523. Xác định tốc độ tối đa để xe có thể đi vào đoạn đường cung tròn an toàn.
Lời giải:
Để có thể đi xe vào đoạn đường cung tròn an toàn, lực ma sát cần có độ lớn bằng với lực hướng tâm. Do đó, tốc độ tối đa của xe là:
Fms = Fht ⇔ μ.N =m.\(\frac{v^{2} }{R}\) ⇔ μ.m.g = m.\(\frac{v^{2} }{R}\)
⇒v = \(\sqrt{μ.g.R}\) = \(\sqrt{0,523.10.35}\) ≈ 13,53 m/s
Vận dụng trang 133 SGK Lý 10 CTST
Khi xe chạy theo đường vòng cung nằm ngang, tốc độ tối đa của xe để giữ an toàn phụ thuộc như thế nào vào hệ số ma sát nghỉ và bán kính đường tròn? Tốc độ này có phụ thuộc trọng lượng của xe không? Từ đó, hãy đề xuất những yếu tố quan trọng cần lưu ý khi thiết kế cầu đường có hình vòng cung.
Lời giải:
Ta có:
Fms = Fht ⇔ μ.N = m.\(\frac{v^{2} }{R}\) ⇔ μ.m.g = m.\(\frac{v^{2} }{R}\)⇒ v = \(\sqrt{μ.g.R}\)
- Tốc độ tối đa của xe để giữ an toàn tỉ lệ với căn bậc 2 của hệ số ma sát nghỉ và bán kính đường tròn.
- Tốc độ này không phụ thuộc vào trọng lượng của xe.
- Một số lưu ý khi thiết kế cầu đường có hình vòng cung là: tăng bán kính và độ nhám của cung đường; làm mặt đường nghiêng 1 góc nhất định với phương ngang để tạo lực hướng tâm.
Bài tập 1 trang 134 SGK Lý 10 CTST
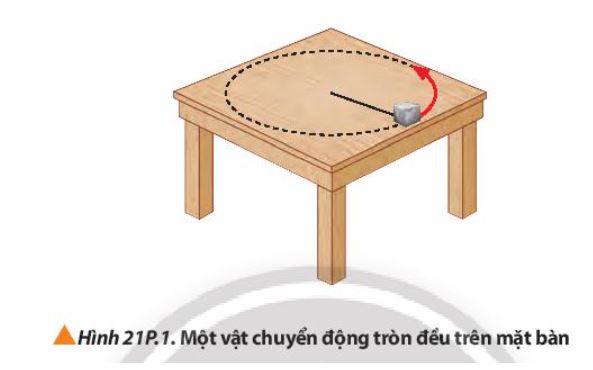
Một đầu của dây nhẹ dài 0,80 m được buộc một vật có khối lượng 3,00 kg. Vật chuyển động tròn đều quanh đầu kia của dây trên mặt bàn nằm ngang (Hình 21P.1). Giả sử không có ma sát giữa vật và mặt bàn. Khi tốc độ quay của dây là 1,6 vòng/s thì dây đứt. Tính lực căng dây lớn nhất.
Lời giải:
Trong trường hợp này, lực căng dây đóng vai trò là lực hướng tâm.
Fht = m.aht = m.ω2.R = m.\(\frac{v^{2} }{R}\)
Do vật có khối lượng và bán kính chuyển động của vật xung quanh bàn không đổi, nên lực căng dây phụ thuộc vào tốc độ góc. Lực căng dây lớn nhất khi tốc độ góc lớn nhất.
ωmax = 1,6 vòng/s = 1,6.2π = 10 rad/s.
Tmax = Fht max = m.ωmax2.R = 3.102.0,8 = 240 N.
Bài tập 2 trang 134 SGK Lý 10 CTST
Mô hình đơn giản của nguyên tử hydrogen giả sử rằng electron chuyển động tròn đều quanh hạt nhân với tốc độ bằng 2,2.106 m/s. Quỹ đạo chuyển động có bán kính bằng 0,53.10-10 m. Hãy tính độ lớn của lực tương tác giữa electron và hạt nhân.
Lời giải:
Lực tương tác giữa các electron và hạt nhân đóng vai trò là lực hướng tâm.
Fht = m.\(\frac{v^{2} }{R}\) = 9,1.10−31.\(\frac{(2,2.10^{6})^{2} }{0,53.10^{10} }\) ≈ 8,31.10−8 N
Bài tập 3 trang 134 SGK Lý 10 CTST
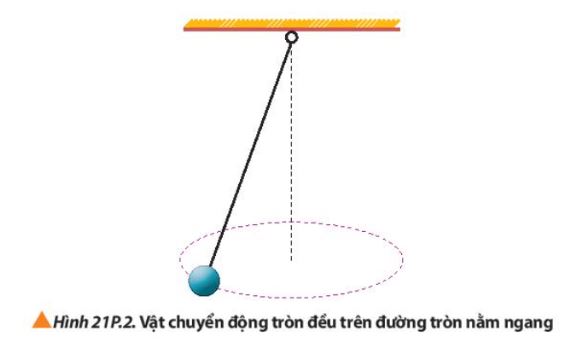
Một vật nặng có kích thước nhỏ, có khối lượng 0,50 kg, được buộc vào đầu một dây có chiều dài 1,5 m. Vật chuyển động đều trên đường tròn nằm ngang (Hình 21P.2). Cho biết dây chỉ chịu được lực căng tối đa bằng 50 N. Hãy tính tốc độ quay lớn nhất của vật để dây không bị đứt.
Lời giải:
Gọi góc hợp bởi phương của sợi dây và phương thẳng đứng là \(\alpha\)
Khi vật chuyển động tròn, hình chiếu lực căng dây trên mặt ngang đóng vai trò là lực hướng tâm.
Fht = T. sinα ⇔ mω2R
⇒ω = \(\sqrt{\frac{T}{m.l} }\) = \(\sqrt{\frac{50}{0,5.1,5} }\) ≈ 8,16 rad/s
Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Giải Lý 10 Bài 21: Động học học của chuyển động tròn. Lực hướng tâm CTST. Hi vọng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Vật lý 10 CTST. Mời các bạn cùng tham khảo thêm tài liệu học tập môn Toán 10 CTST...
