Giải Lý 10 Bài 9: Chuyển động thẳng biến đổi đều KNTT

Giải Vật lý 10 Kết nối tri thức

1 508

Giải Lý 10 Bài 9 KNTT

Bài 1 trang 43 SGK Vật lý 10 Kết nối tri thức
Bài 2 trang 43 SGK Vật lý 10 Kết nối tri thức

VnDoc.com xin gửi tới bạn đọc bài viết Giải Lý 10 Bài 9: Chuyển động thẳng biến đổi đều KNTT để bạn đọc cùng tham khảo. Mời các bạn cùng theo dõi nội dung giải SGK Vật lý 10 Kết nối tri thức dưới đây nhé.

Bài 1 trang 43 SGK Vật lý 10 Kết nối tri thức

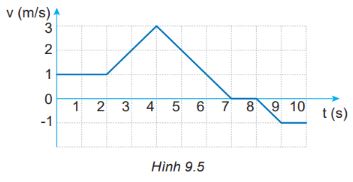
Đồ thị vận tốc – thời gian ở Hình 9.5 mô tả chuyển động của một chú chó con đang chạy trong ngõ thẳng và hẹp.

a) Hãy mô tả chuyển động của chú chó.

b) Tính quãng đường đi được và độ dịch chuyển của chú chó sau 2s; 4s; 7s và 10s bằng đồ thị và bằng công thức.

Giải Lý 10 Bài 9

Lời giải

a) Mô tả chuyển động:

- Từ giây thứ 0 đến giây thứ 2: chuyển động thẳng đều với vận tốc 1 m/s.

- Từ giây thứ 2 đến giây thứ 4: chuyển động thẳng nhanh dần đều từ 1 m/s đến 3 m/s.

- Từ giây thứ 4 đến giây thứ 7: chuyển động chậm dần đều từ 3 m/s về 0 m/s.

- Từ giây thứ 7 đến giây thứ 8: đứng yên.

- Từ giây thứ 8 đến giây thứ 9: chuyển động thẳng nhanh dần đều theo chiều ngược lại (theo chiều âm).

- Từ giây thứ 9 đến giây thứ 10: chuyển động thẳng đều theo chiều âm.

b) Tính quãng đường và độ dịch chuyển bằng đồ thị

- Sau 2 giây:

+ Quãng đường: s₁ = 1.2 = 2m

+ Độ dịch chuyển: d₁ = 1.2 = 2m

- Sau 4 giây:

+ Quãng đường: s₂ = s₁ + $\frac12$ .(1 + 3).2 = 6m

+ Độ dịch chuyển: d₂ = d₁ + $\frac12$ .(1 + 3).2 = 6m

- Sau 7 giây:

+ Quãng đường: s₃ = s₂ + $\frac12$ .3.3 = 10,5m

+ Độ dịch chuyển: d₃ = d₂ + $\frac12$ .3.3 = 10,5m

- Sau 10 giây:

+ Từ giây thứ 7 đến giây thứ 8 vật đứng yên nên quãng đường bằng 0.

+ Quãng đường: s₄ = s₃ + $\frac12$ .1.1 + 1.1 = 12m

+ Độ dịch chuyển: d₄ = d₃ + $\frac12$ .(-1).1 + (-1).1 = 9m

Tính quãng đường và độ dịch chuyển bằng công thức:

Giải Lý 10 bài 9

- Sau 2 giây:

+ Độ dịch chuyển: d₁ = v₀t₁ = 1.2 = 2m

+ Vật chuyển động thẳng không đổi chiều nên quãng đường bằng độ dịch chuyển: s₁ = d₁ = 2m

- Sau 4 giây:

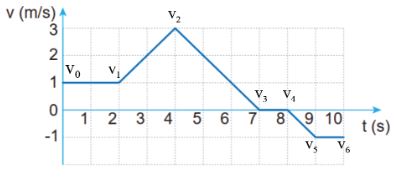
+ Gia tốc tính từ giây thứ 2 đến giây thứ 4: $a_1\;=\;\frac{v_2\;-\;v_1}{4\;-\;2}\;=\;\frac{3-1}{4-2}\;=\;1\;m/s^2$

+ Độ dịch chuyển:

$d_2\;=\;d_1\;+\;v_1\;t_2\;+\;\frac12\;a_1\;t_2^2\;=\;2\;+\;1\;.\;2\;+\;\frac12\;.\;1\;.\;2^2\;=\;6\;m$

+ Vật chuyển động thẳng không đổi chiều nên quãng đường bằng độ dịch chuyển: s₂ = d₂ = 6m

- Sau 7 giây:

+ Gia tốc tính từ giây thứ 4 đến giây thứ 7: $a_2\;=\;\frac{v_3\;-\;v_2}{7\;-\;4}\;=\;\frac{0\;-\;3}{7\;-\;4}\;=\;-1\;m/s^2$

+ Độ dịch chuyển: $d_3\;=\;d_2\;+\;v_2\;t_3\;+\;\frac12\;a_2\;t_3^2\;=\;6\;+\;3\;.\;3\;+\;\frac12\;.\;(-1)\;.\;3^2\;=\;10,5\;m$

+ Vật chuyển động thẳng không đổi chiều nên quãng đường bằng độ dịch chuyển: s₃ = d₃ = 10,5m

- Sau 10 giây:

+ Từ giây thứ 7 đến giây thứ 8 vật đứng yên nên quãng đường bằng 0.

+ Từ giây thứ 8 đến giây thứ 9 vật chuyển động theo chiều âm

+ Gia tốc tính từ giây thứ 8 đến giây thứ 9: $a_3\;=\;\frac{v_5\;-\;v_4}{9\;-\;8}\;=\;\frac{-\;1\;-\;0}{9\;-\;8}\;=\;-1\;m/s^2$

+ Độ dịch chuyển từ giây thứ 8 đến giây thứ 9: $d_4\;=\;v_4\;t_5\;+\;\frac12\;a_3\;t_5^2\;=\;0\;.\;1\;+\;\frac12\;.\;(-1)\;.\;1^2\;=\;-\;0,5\;m$

+ Quãng đường vật đi được từ giây thứ 8 đến giây thứ 9 là: s' = 0,5m

+ Từ giây thứ 9 đến giây thứ 10 vật chuyển động thẳng đều nên gia tốc bằng 0

+ Độ dịch chuyển từ giây thứ 9 đến giây thứ 10: d₅ = v₅t₆ = (-1) . 1 = -1m

+ Quãng đường vật đi được từ giây thứ 9 đến giây thứ 10 là: s'' = 1m

+ Độ dịch chuyển sau 10 giây: d = d₃ + d₄ + d₅ = 10,5 - 0,5 - 1 = 9m

+ Quãng đường sau 10 giây: s = s₃ + s₄ + s₅ = 10,5 + 0,5 + 1 = 12m

Bài 2 trang 43 SGK Vật lý 10 Kết nối tri thức

Một vận động viên đua xe đạp đường dài vượt qua vạch đích với tốc độ 10 m/s. Sau đó vận động viên này đi chậm dần đều thêm 20 m mới dừng lại. Coi chuyển động của vận động viên là thẳng.

a) Tính gia tốc của vận động viên trong đoạn đường sau khi qua vạch đích.

b) Tính thời gian vận động viên đó cần để dừng lại kể từ khi cán đích.

c) Tính vận tốc trung bình của người đó trên quãng đường dừng xe.

a)

Áp dụng công thức: $v^2\;-\;v_0^2\;=\;2ad$

Gia tốc của vận động viên trong đoạn đường sau khi qua vạch đích (khi dừng lại v = 0) là

$a\;=\;\frac{v^2\;-\;v_0^2}{2d}\;=\;\frac{0^2\;-\;10^2}{2\;.\;20}\;=\;-\;2,5\;m/s^2$

b) Thời gian vận động viên cần để dựng lại kể từ khi cán đích là:

$t\;=\;\frac{v\;-\;v_0}a\;=\;\frac{0\;-\;10}{-\;2,5}\;=\;4s$

c) Vận tốc trung bình của người đó trên quãng đường dừng xe là:

$v_{tb}\;=\;\frac{v\;+\;v_0}2\;=\;\frac{0\;+\;10}2\;=\;5\;m/s$

Hoặc có thể áp dụng công thức: $v_{tb}\hspace{0.278em}=\;\frac dt\;=\;\frac{20}4\;=\;5\;m/s\hspace{0.278em}$

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Giải Lý 10 Bài 9: Chuyển động thẳng biến đổi đều KNTT. Hi vọng qua bài viết này bạn đọc có thêm nhiều tài liệu để học tập tốt hơn môn Vật lý 10 KNTT. Mời các bạn cùng tham khảo thêm tài liệu học tập các môn Toán 10 KNTT, Hóa học 10 KNTT