Một số cách tính nhẩm nhanh và chính xác
Một số cách tính nhẩm môn Toán nhanh và chính xác
Tính nhẩm toán nhanh và chính xác là cách học môn Toán rất hay. Với nhiều bài toán, chúng ta không cần sử dụng máy tính cũng có thể giải được dễ dàng bằng những phương pháp tính nhanh, những quy luật toán học đơn giản mà bạn không thể tìm thấy trong sách giáo khoa. Hãy cùng VnDoc.com tham khảo một số cách tính nhẩm nhanh và chính xác để biết thêm các mẹo tính nhẩm nhanh mà không cần dùng máy tính.
Trong quá trình làm toán, ta thường gặp những bài toán tính mà nếu để ý và biết thêm một số "mẹo" thì ta tính rất nhanh. Đỡ mất thời gian so với cách tính thuần túy. Sau đây là một số ví dụ:

1. Làm phép trừ bằng cách cộng
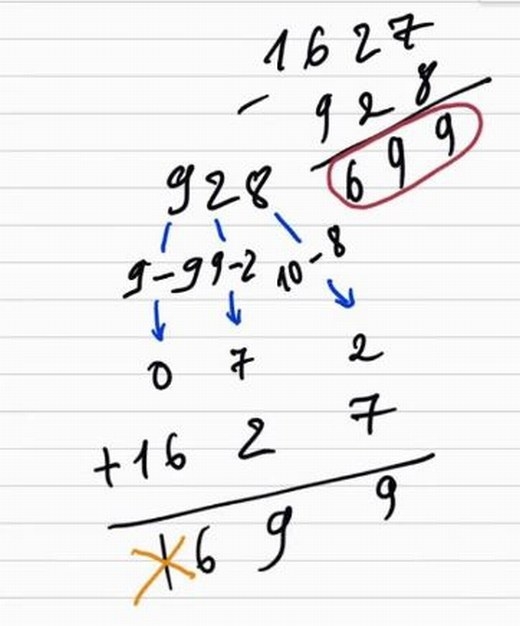
Bạn có biết rằng tính nhẩm phép trừ bằng phép cộng sẽ đơn giản hơn. Không tin, ta có thể làm theo cách dưới đây.
Ví dụ như 1627 – 928. Đầu tiên ta lấy số 9 trừ đi các số nằm trong số bị trừ, riêng số đơn vị lấy số 10 để trừ. Kết quả sẽ là 072, tức 72.
Bước tiếp theo, lấy số vừa có cộng với số trừ, tức cộng với 1627, ta được số 1699. Cuối cùng, lấy số đầu tiên trừ đi 1 ta được kết quả.
2. Bình phương một số có 2 chữ số
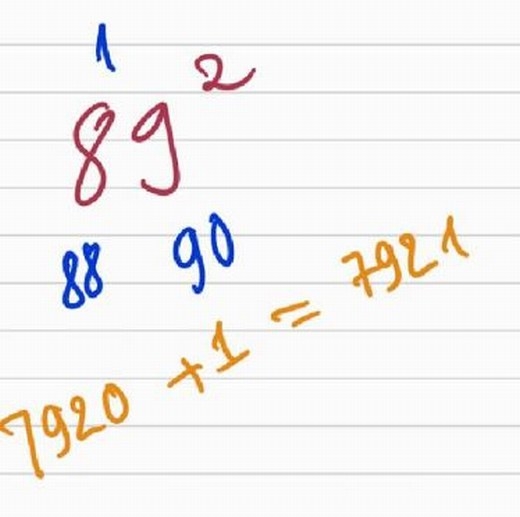
Bạn có bao giờ thử bình phương một con số nào đó có hai chữ số trở lên bằng cách tính nhẩm, sẽ rất khó phải không nào? Nhưng nếu áp dụng cách dưới đây sẽ đơn giản hơn.
Ví dụ với bình phương của số 89. Đầu tiên, ta lấy số tròn chục gần nhất của số đó, với 89 là 90. Tiếp đó, lấy số tròn chục này trừ đi số đang có, tức 90 – 89 = 1.
Tiếp theo, lấy số hiện có trừ đi số ta vừa tìm ra, tức 89 – 1 = 88. Lấy tích của hai số mới là 88 x 90 = 7920.
Tiếp theo, lấy số đó cộng thêm kết quả bình phương của số tròn chục trừ đi số cần bình phương, tức 12 = 1.
Lấy số 7920 + 1 = 7921, ta có kết quả cuối cùng.
Công thức này đúng với mọi số, tuy nhiên để tính nhẩm, ta nên áp dụng với số có hai chữ số.
3. Nhân số có 2 chữ số với nhau
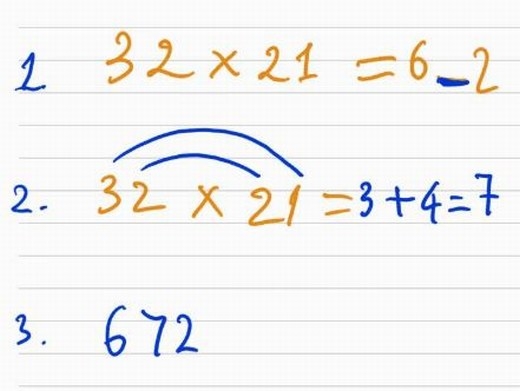
Bạn có thể nhẩm tính tích của số có 2 chữ số với nhau bằng cách dưới đây.
Ví dụ với 32 x 21. Đầu tiên, ta lấy số hàng chục nhân với số hàng chục, số hàng đơn vị nhân với số hàng đơn vị và đặt dấu gạch ở giữa. Ở đây sẽ là 6_2.
Tiếp đó, bạn lấy số hàng chục của số thứ nhất nhân với số hàng đơn vị của số thứ hai và lấy số hàng đơn vị của số thứ hai nhân với số hàng chục của số thứ nhất. Tiếp đó, tính tổng 2 số, ở đây là (3 x 1) + (2 x 2) = 3 + 4 = 7.
Điền số 7 vào dấu "_" ta có kết quả cuối cùng.
4. Bình phương nhanh số có số tận cùng là 5

Nếu muốn tính bình phương của một số có hai chữ số có số tận cùng là 5, ta có thể lấy chữ số hàng chục nhân với số đó cộng thêm 1, được kết quả bao nhiêu thì viết thêm 25 phía sau. Ví dụ: 952 = 9 x (9+1) viết thêm 25 = 9025.
5. Nhân nhẩm hai số có chữ số hàng chục giống nhau, chữ số hàng đơn vị có tổng bằng 10
Xét tích hai chữ số hàng đơn vị viết vào tận cùng của tích rồi nhân chữ số hàng chục với số liền sau của chữ số ấy được tích viết vào trước tích của hai chữ số hàng đơn vị. Ta được tích đúng.
Ví dụ:
|
a) 67 x 63 = ? 4221 Nhẩm: 3 x 7 = 21 6 x 7 = 42 Vậy 67 x 63 = 4221 |
b) 94 x 96 = ? 9024 Nhẩm: 4 x 6 = 24 9 x 10 = 90 Vậy 94 x 96 = 9024 |
6. Nhân nhẩm số có hai chữ số với số có hai chữ số đối xứng nhau qua một số tròn chục
Xét bình phương của số tròn chục gần nhất giữa hai số rồi trừ đi bình phương số đơn vị của thừa số bị giảm đi hay tăng lên đến số tròn chục. Ta được tích đúng.
Ví dụ:
|
a) 52 x 48 = ? 2496 Nhẩm: 50 x 50 = 2500 2 x 2 = 4 Vậy 52 x 48 = 2500 - 4 = 2496. |
b) 68 x 52 = ? 3536 Nhẩm: 60 x 60 = 3600 8 x 8 = 64 Vậy 68 x 52 = 3600 - 64 = 3536. |
|
c) 46 x 54 = ? 2484 Nhẩm: 50 x 50 = 2500 4 x 4 = 16 Vậy 46 x 54 = 2500 - 16 = 2484. |
đ) 71 x 89 = ? 6319 Nhẩm: 80 x 80 = 6400 9 x 9 = 81 Vậy 71 x 89 = 6400 - 81 = 6319. |
Cách tính nhân 2 chữ số của người Nhật
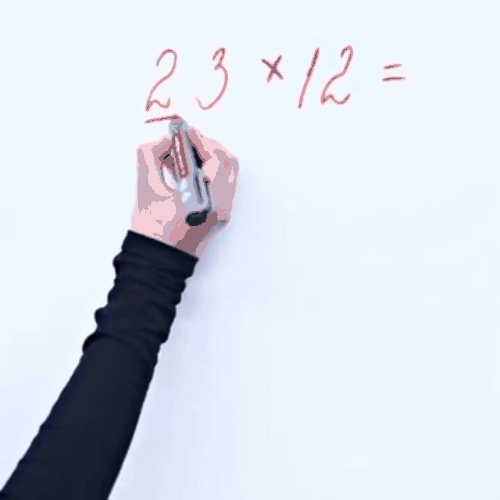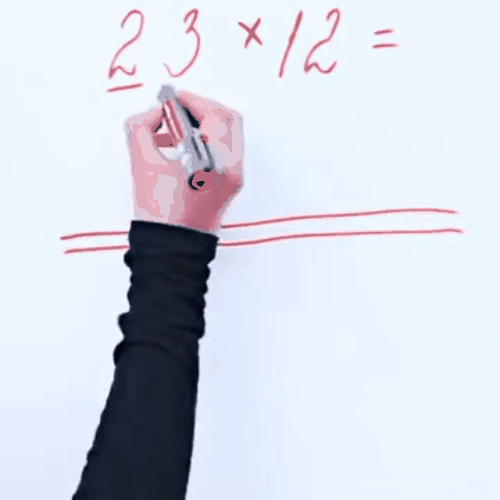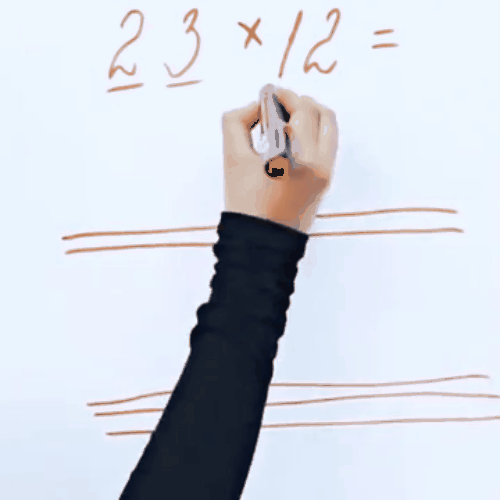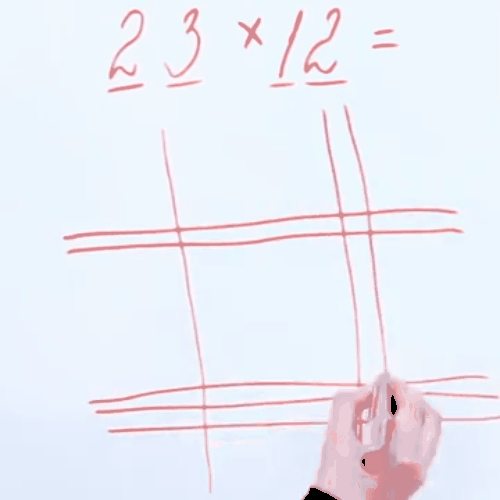
Đầu tiên, chúng ta thể hiện số có hai chữ số bằng các đường thẳng kẻ ngang và cho chúng giao nhau phải không nào?
Việc để cho 2 đường thẳng giao với 3 đường thẳng chính là phép nhân 2 x 3 = 6, và nó sẽ tương ứng với 6 điểm giao nhau.
Tương tự, phần giao nhau giữa 2 đường thẳng với 2 đường thẳng và một đường thẳng với 3 đường thẳng, thực ra chính là phép tính: (2 x 2) + (1 x 3) = 7
Và số 2 đứng đầu chính là 1 x 2 = 2.
Cùng so sánh khi ta đặt phép tính nhân theo kiểu thông thường nhé!
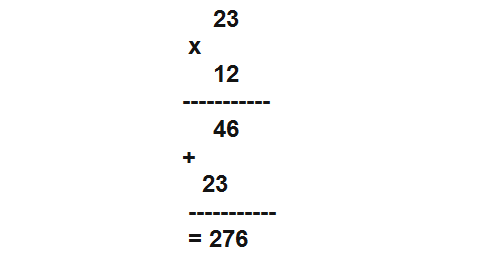
Kết quả "y xì đúc" nhau phải không?
Mặc dù nhiều bạn cho rằng, phương pháp này có phần hơi rắc rối, khi đặt hàng dọc tính như bình thường nhanh hơn, nhưng nó sẽ cực hữu hiệu ở các phép tính lớn đấy! Không tin bạn thử thì biết!

