Tổng hợp đề thi và lời giải đề trường Đông ba miền 2015
Tổng hợp đề thi và lời giải đề trường Đông ba miền 2015
Tổng hợp đề thi và lời giải đề trường Đông ba miền 2015 là tài liệu ôn thi học sinh giỏi quốc gia môn Toán hay dành cho quý thầy cô và các bạn học sinh tham khảo. Hi vọng tài liệu này sẽ giúp các bạn ôn luyện, chuẩn bị về hành trang kiến thức lẫn kỹ năng làm bài thi để có thể mang về kết quả tốt nhất.
Đề thi học sinh giỏi quốc gia THPT môn Toán năm 2016
Đề số 1.
Đề thi trường Đông miền Bắc (Hà Nội)
Đề thi ngày 1.
Bài 1. (5 điểm).
Tìm tất cả các hàm số f: R → R thỏa mãn đồng thời các điều kiện sau:
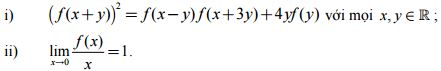
Bài 2. (5 điểm).
Cho tam giác ABC có đường tròn nội tiếp (I) tiếp xúc AC, AB lần lượt tại E, F. Gọi G, H theo thứ tự là các điểm đối xứng với E, F qua I. Giả sử GH cắt BC tại P. Các điểm M, N thuộc IP sao cho CM vuông góc với IB và BN vuông góc với IC. Chứng
minh rằng I là trung điểm MN.
Bài 3. (5 điểm).
Chứng minh rằng với mọi số thực không âm a, b, c trong đó không có hai số nào đồng thời bằng 0 ta có bất đẳng thức
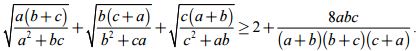
Bài 4. (5 điểm).
Trên bàn cờ 8x8, ta đặt các quân xe màu xanh, đỏ, vàng sao cho các quân xe khác màu không ăn nhau. Hỏi có thể đặt tối đa được bao nhiêu quân xe như vậy nếu biết rằng số quân xe mỗi màu giống nhau?
Đề thi trường Đông miền Bắc (Hà Nội)
Đề thi ngày 2.
Bài 5. (6 điểm).
Dãy đa thức Pn(x, y, z) được xác định như sau:
![]()
Chứng minh rằng Pn(x, y, z) là đa thức đối xứng với mọi n.
Bài 6. (7 điểm).
Cho tam giác ABC cân tại A có P nằm trong tam giác sao cho góc BPC = 1800 - góc A. Các đường thẳng PB, PC lần lượt cắt CA, AB tại E, F. Gọi I, J lần lượt là tâm bàng tiếp ứng với đỉnh B, C của tam giác ABE và ACF. Gọi K là tâm ngoại tiếp tam giác AEF. Chứng minh rằng KI = KJ.
Bài 7. (7 điểm).
Tìm tất cả các số nguyên dương k sao cho phương trình x2 - (k2 - 4)y2 + 24 = 0 có nghiệm nguyên dương.
Mời các bạn tải file đầy đủ về tham khảo!



