Cách tính lực tương tác của nhiều điện tích điểm
Cách tính lực tương tác của nhiều điện tích điểm
Trong thế giới vi mô, các điện tích không tồn tại riêng lẻ mà thường tương tác đồng thời với nhiều điện tích khác. Vậy làm thế nào để xác định lực tương tác tổng hợp tác dụng lên một điện tích điểm từ nhiều điện tích xung quanh? Bài viết này sẽ hướng dẫn bạn cách tính lực tương tác của nhiều điện tích điểm bằng cách áp dụng nguyên lý chồng chất lực, kết hợp định luật Coulomb, cùng với các ví dụ minh họa dễ hiểu giúp bạn nắm vững kiến thức trọng tâm trong chương trình vật lý phổ thông.
A. Hợp lực do nhiều điện tích tác dụng lên một điện tích
Phương pháp: Các bước tìm hợp lực 
\({\overrightarrow{F}}_{o}\) do các điện tích q1; q2; ... tác dụng lên điện tích qo:
- Bước 1: Xác định vị trí điểm đặt các điện tích (vẽ hình).
- Bước 2: Tính độ lớn các lực \(F_{10};F_{20}...\) , Fno lần lượt do q1 và q2 tác dụng lên qo.
- Bước 3: Vẽ hình các vectơ lực \({\overrightarrow{F}}_{10};{\overrightarrow{F}}_{20}\)....\(\overset{⃑}{F_{n0}}\)
- Bước 4: Từ hình vẽ xác định phương, chiều, độ lớn của hợp lực \({\overrightarrow{F}}_{o}\).
Góc \(\alpha\) bất kì: \(\alpha\) là góc hợp bởi hai vectơ lực.
\(F_{0}^{2} = F_{10}^{2} + F_{20}^{2} +
2F_{10}^{}F_{20}^{}.cos\alpha\)
Các trường hợp đặc biệt:
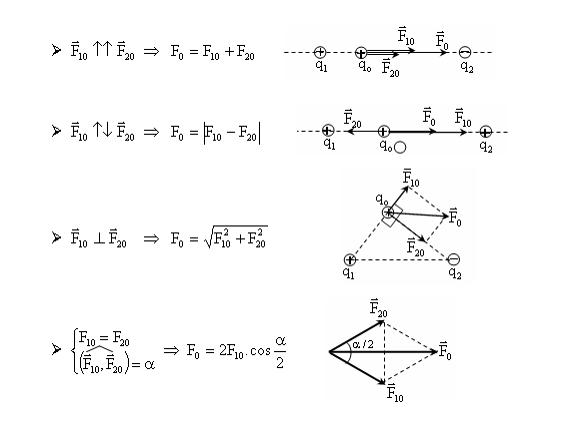
2. Bài tập tính lực tương tác của nhiều điện tích điểm
Ví dụ: Trong chân không, cho hai điện tích \(q_{1}
= - q_{2} = 10^{- 7}C\) đặt tại hai điểm A và B cách nhau 8cm. Tại điểm C nằm trên đường trung trực của AB và cách AB 3cm người ta đặt điện tích \(q_{o} = 10^{- 7}C\). Xác định lực điện tổng hợp tác dụng lên qo.
Tóm tắt:
\(\begin{matrix}
q_{1} = 10^{- 7}C \\
q_{2} = - 10^{- 7}C \\
\end{matrix}\)
\(q_{o} = 10^{- 7}C;AB = 8cm;AH =
3cm\)
--------------------------------------
\({\overrightarrow{F}}_{o} = ?\)
Giải:
Vị trí các điện tích như hình vẽ.
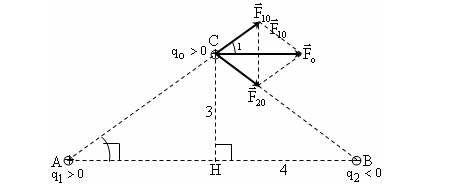
+ Lực do q1 tác dụng lên qo:
\(F_{10} = k\frac{\left| q_{1}q_{0}
\right|}{AC^{2}} = 9.10^{9}\frac{\left| 10^{- 7}.10^{- 7}
\right|}{0,05^{2}} = 0,036N\)
+ Lực do q2 tác dụng lên qo:
\(F_{20} = F_{10} = 0,036N\)( do \(\left| q_{1} \right| = \left| q_{2}
\right|\))
+ Do \(F_{20} = F_{10}\) nên hợp lực Fo tác dụng lên qo:
\(\begin{matrix}
F_{o} = 2F_{10}.cosC_{1} = 2.F_{10}.cosA = 2.F_{10}.\frac{AH}{AC} \\
F_{o} = 2.0,036.\frac{4}{5} = 57,6.10^{- 3}N \\
\end{matrix}\)
+ Vậy \({\overrightarrow{F}}_{o}\) có phương // AB, cùng chiều với vectơ \(\overrightarrow{AB}\) (hình vẽ) và có độ lớn: \(F_{o} = 57,6.10^{- 3}N\)
3. Bài tập vận dụng tính lực tương tác của nhiều điện tích điểm
Bài 1. Cho hai điện tích điểm \(q_{1} =
2.10^{- 7}C;q_{2} = - 3.10^{- 7}C\)đặt tại hai điểm A và B trong chân không cách nhau 5cm. Xác định lực điện tổng hợp tác dụng lên \(q_{o} = - 2.10^{- 7}C\)trong hai trường hợp:
a. \(q_{o}\)đặt tại C, với CA = 2cm; CB = 3cm.
b. \(q_{o}\)đặt tại D với DA = 2cm; DB = 7cm.
ĐS: a. \(F_{o} = 1,5N\); b. \(F = 0,79N\).
Bài 2. Hai điện tích điểm \(q_{1} = 3.10^{-
8}C;q_{2} = 2.10^{- 8}C\) đặt tại hai điểm A và B trong chân không, AB = 5cm. Điện tích \(q_{o} = - 2.10^{-
8}C\)đặt tại M, MA = 4cm, MB = 3cm. Xác định lực điện tổng hợp tác dụng lên \(q_{o}\).
ĐS: \(F_{o} \approx 5,23.10^{-
3}N\).
Bài 3. Trong chân không, cho hai điện tích \(q_{1} = q_{2} = 10^{- 7}C\) đặt tại hai điểm A và B cách nhau 10cm. Tại điểm C nằm trên đường trung trực của AB và cách AB 5cm người ta đặt điện tích \(q_{o}
= 10^{- 7}C\). Xác định lực điện tổng hợp tác dụng lên qo.
ĐS: \(F_{o} \approx
0,051N\).
Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!
---------------------------------
Việc hiểu và áp dụng đúng cách tính lực tương tác của nhiều điện tích điểm sẽ giúp bạn giải quyết hiệu quả các bài toán phức tạp trong điện học. Hy vọng bài viết đã cung cấp cho bạn nền tảng kiến thức vững chắc và công cụ cần thiết để chinh phục mọi dạng bài liên quan đến lực tĩnh điện. Hãy tiếp tục luyện tập để thành thạo kỹ năng này và nâng cao tư duy vật lý của bạn!
