Tổng hợp Công thức dao động Con lắc lò xo cần nhớ

Con lắc lò xo là một trong những phần quan trọng trong chuyên đề dao động điều hòa của chương trình Vật Lý 11. Việc ghi nhớ và vận dụng đúng các công thức dao động con lắc lò xo là chìa khóa để giải nhanh, chính xác các dạng bài tập trong đề kiểm tra và đề thi THPT Quốc Gia. Trong bài viết này, chúng tôi sẽ tổng hợp toàn bộ công thức con lắc lò xo cần nhớ, được hệ thống logic, ngắn gọn, dễ hiểu và dễ tra cứu. Bài viết phù hợp cho cả học sinh đang học và ôn thi, hỗ trợ bạn tiết kiệm thời gian và tối ưu hiệu quả học tập.

I. Con lắc lò xo

Gồm một vật nhỏ khối lượng m gắn vào đầu lò xo độ cứng k, khối lượng lò xo không đáng kể

II. Khảo sát dao động con lắc lò xo về mặt động lực học 

• Hướng về vị trí cân bằng
• Biến thiên điều hoà theo thời gian với cùng chu kỳ của li độ
•  Ngược pha với li độ

III. Khảo sát dao động con lắc lò xo về mặt năng lượng

- Cơ năng của con lắc tỉ lệ với bình phương biên độ dao động

- Cơ năng của con lắc được bảo toàn nếu bỏ qua ma sát

- Động năng và thế năng biến thiên tuần hoàn với tần số góc 2ω, tần số 2f, chu kỳ T/2

- Thời gian liên tiếp giữa 2 lần động năng bằng thế năng là T/4

- Khi \(W_{đ} = nW_{t} \rightarrow x =\frac{\pm A}{\sqrt{n^{} + 1}}\)

- Khi\(W_{t} = nW_{đ} \rightarrow v =\frac{\pm A\omega}{\sqrt{n^{} + 1}}\)

IV. Các dạng bài tập con lắc lò xo

1. * Độ biến dạng của lò xo thẳng đứng khi vật ở VTCB:

\(\Delta l = \frac{mg}{k}\)⇒\(T = 2\pi\sqrt{\frac{\Delta l}{g}}\)

* Độ biến dạng của lò xo khi vật ở VTCB với con lắc lò xo nằm trên mặt phẳng nghiêng có góc nghiêng α:

\(\Delta l = \frac{mg\sin\alpha}{k}\)⇒\(T = 2\pi\sqrt{\frac{\Delta l}{g\sin\alpha}}\)

+ Chiều dài lò xo tại VTCB: l_CB = l₀ + ∆l (l₀ là chiều dài tự nhiên)

+ Chiều dài cực tiểu (khi vật ở vị trí cao nhất): l_Min = l₀ + ∆l – A

+ Chiều dài cực đại (khi vật ở vị trí thấp nhất): l_Max = l₀ + ∆l + A

⇒ l_CB = (l_Min + l_Max)/2

+ Khi A >∆l (Với Ox hướng xuống):

- Thời gian lò xo nén 1 lần là thời gian ngắn nhất để vật đi từ vị trí x₁ = -∆l đến x₂ = -A.

- Thời gian lò xo giãn 1 lần là thời gian ngắn nhất để vật đi từ vị trí x₁ = -∆l đến x₂ = A.

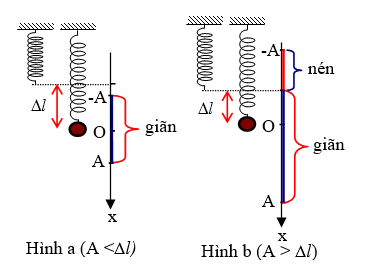
Lưu ý: Trong một dao động (một chu kỳ) lò xo nén 2 lần và giãn 2 lần

2. Lực kéo về hay lực hồi phục F = -kx = -mω²x

Đặc điểm:

• Là lực gây dao động cho vật.
• Luôn hướng về VTCB
• Biến thiên điều hoà cùng tần số với li độ

3. Lực đàn hồi là lực đưa vật về vị trí lò xo không biến dạng.

Có độ lớn F_đh = kx (x là độ biến dạng của lò xo)

* Với con lắc lò xo nằm ngang thì lực kéo về và lực đàn hồi là một (vì tại VTCB lò xo không biến dạng)

* Với con lắc lò xo thẳng đứng hoặc đặt trên mặt phẳng nghiêng

+ Độ lớn lực đàn hồi có biểu thức:

* F_đh = k|∆l + x| với chiều dương hướng xuống

* F_đh = k|∆l - x| với chiều dương hướng lên

+ Lực đàn hồi cực đại (lực kéo): F_Max = k(∆l + A) = F_Kmax (lúc vật ở vị trí thấp nhất)

+ Lực đàn hồi cực tiểu:

* Nếu A < ∆l ⇒ F_Min = k(∆l - A) = F_KMin

* Nếu A ≥ ∆l ⇒ F_Min = 0 (lúc vật đi qua vị trí lò xo không biến dạng)

Lực đẩy (lực nén) đàn hồi cực đại: F_Nmax = k(A - ∆l) (lúc vật ở vị trí cao nhất)

Lực đàn hồi, lực hồi phục:

a. Lực đàn hồi: \(F_{ñh} = k(\Delta l + x)\)

\(\Rightarrow \left\{ \begin{matrix} F_{ñhM} = k(\Delta l + A)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ F_{ñhm} = k(\Delta l - A)\ neu\ \Delta l > A \\ F_{ñhm} = 0\ neu\ \Delta l \leq A\ \ \ \ \ \ \ \ \ \ \ \ \ \end{matrix} \right.\ \ \ \ \ \\)

b. Lực hồi phục: \(F_{hp} = kx\ \Rightarrow \left\{ \begin{matrix} F_{hpM} = kA \\ F_{hpm} = 0\ \end{matrix} \right.\ \ \ \ \ \\)hay\(F_{hp} = ma\ \Rightarrow \left\{ \begin{matrix} F_{hpM} = m\omega^{2}A \\ F_{hpm} = 0\ \ \ \ \ \ \ \ \end{matrix} \right.\) lực hồi phục luôn hướng vào vị trí cân bằng.

Chú ý: Khi hệ dao động theo phương nằm ngang thì lực đàn hồi và lực hồi phục là như nhau

4. Một lò xo có độ cứng k, chiều dài l được cắt thành các lò xo có độ cứng k₁, k₂, … và chiều dài tương ứng là l₁, l₂, … thì có: kl = k₁l₁ = k₂l₂ = …

5. Ghép lò xo

* Nối tiếp \(\frac{1}{k} = \frac{1}{k_{1}} + \frac{1}{k_{2}} + ...\) ⇒ cùng treo một vật khối lượng như nhau thì: T² = T₁² + T₂²

* Song song: k = k₁ + k₂ + … ⇒ cùng treo một vật khối lượng như nhau thì:\(\frac{1}{T^{2}} = \frac{1}{T_{1}^{2}} + \frac{1}{T_{2}^{2}} + ...\)

6. Gắn lò xo k vào vật khối lượng m₁ được chu kỳ T₁, vào vật khối lượng m₂ được T₂, vào vật khối lượng m₁+m₂ được chu kỳ T₃, vào vật khối lượng m₁ – m₂ (m₁ > m₂) được chu kỳ T₄.

Thì ta có: \(T_{3}^{2} = T_{1}^{2} + T_{2}^{2}\) và \(T_{4}^{2} = T_{1}^{2} - T_{2}^{2}\).

7. Đo chu kỳ bằng phương pháp trùng phùng

Để xác định chu kỳ T của một con lắc lò xo (con lắc đơn) người ta so sánh với chu kỳ T₀ (đã biết) của một con lắc khác (T ≈ T₀).

Hai con lắc gọi là trùng phùng khi chúng đồng thời đi qua một vị trí xác định theo cùng một chiều.

Thời gian giữa hai lần trùng phùng \(\theta = \frac{TT_{0}}{\left| T - T_{0} \right|}\)

Nếu T > T₀ ⇒ θ = (n+1)T = nT₀.

Nếu T < T₀ ⇒ θ = nT = (n+1)T₀. với n ∈ N*

IV. Bài tập minh họa chủ đề Con lắc lò xo

Hướng dẫn giải

a. Ta có: \(\left\{ \begin{matrix} A = 5cm \\ v_{\max} = 50cm/s \end{matrix} \right.\)

\(\Rightarrow v_{\max} = A.\omega \Leftrightarrow \dfrac{5}{100} = 5.\omega\Rightarrow \omega = 10(rad/s)\)

\(W = 5J \Rightarrow k = \dfrac{2W}{A^{2}} = \dfrac{2.0,5}{(0,05)^{2}} = 400(N/m)\)

b. Ta có: \(m = \frac{k}{\omega^{2}} = \frac{400}{10^{2}} = 4(kg)\)

c. Ta có: x = 2cm

\(\begin{matrix} \Rightarrow W_{t} = \frac{1}{2}k.x^{2} = \frac{1}{2}.400.(0,02)^{2} = 0,08(J) \\ \Rightarrow W_{d} = W - W_{t} = 0,5 - 0,08 = 0,42(J) \end{matrix}\)

Hướng dẫn giải

Ta có:

\(T_{1} = 2\pi\sqrt{\frac{m_{1}}{k}}\)\(\Rightarrow T_{1} = 4\pi^{2}\left(\frac{m_{1}}{k} \right)\)

\({T_2} = 2\pi \sqrt {\frac{{{m_2}}}{k}} \Rightarrow {T_1} = 4{\pi ^2}\left( {\frac{{{m_2}}}{k}} \right)\)

\(T = 2\pi\sqrt{\frac{m_{1} + m_{2}}{k}} \Rightarrow T^{2} = 4\pi^{2}\left( \frac{m_{1} + m_{2}}{k} \right)\)

\(\Rightarrow T^{2} = 4\pi^{2}\frac{m_{1}}{k} + 4\pi^{2}\frac{m_{2}}{k} ={T_{1}}^{2} + {T_{2}}^{2}\)

\(\Rightarrow T^{2} = 0,6^{2} + 0,8^{2} = 1(s)\)

Hướng dẫn giải

Ta có: \(W_{t} = 3.W_{d}\)

\(\begin{matrix}\Rightarrow W_{d} = \dfrac{1}{3}.W_{t} \hfill\\\Rightarrow |x| = \dfrac{A}{\sqrt{n + 1}} = \dfrac{A}{\sqrt{\dfrac{1}{3} +1}} = \dfrac{A\sqrt{3}}{2} \hfil\\\Rightarrow |v| = \dfrac{v_{\max}}{2} = \dfrac{\omega.A}{2}\hfil\end{matrix}\)

Mà \(\omega = \sqrt{\frac{k}{m}} = \sqrt{\frac{20}{0,2}} = 10(rad/s)\)

\(\Rightarrow |v| = \frac{10.0,06}{2} = 0,3(m/s)\)

vận tốc của vật khi đi qua vị trí có thế năng bằng 3 động năng.

Vậy khi đi qua vị trí có thế năng bằng 3 động năng vận tốc của vật lad 0,3m/s.

Hướng dẫn giải

Ta có: \(\left\{ \begin{matrix} l_{\max} = l_{0} + A \\ l_{\min} = l_{0} - A \end{matrix} \right.\ \Rightarrow A = \frac{l_{\min} - l_{\max}}{2} = \frac{30 - 22}{2} = 4(cm)\)

Động năng của vật tại x = 3cm

\(W_{d} = W - W_{t} = \frac{1}{2}kA^{2} - \frac{1}{2}kx^{2} = \frac{1}{2}.100.\left( 0,04^{2} - 0,03^{2} \right) = 0,035(J)\)

Đáp án A

-------------------------------------------

Trên đây là toàn bộ công thức dao động của con lắc lò xo quan trọng và thường gặp trong chương trình Vật Lý 11. Việc học thuộc công thức kết hợp với luyện tập bài tập thường xuyên sẽ giúp bạn làm chủ chuyên đề này một cách dễ dàng.

Hãy lưu lại bảng công thức để tiện ôn luyện mỗi ngày. Nếu bạn thấy bài viết hữu ích, đừng ngần ngại chia sẻ cho bạn bè cùng học hoặc tải về dưới dạng file PDF. Chúc bạn học tốt và đạt điểm cao trong các kỳ thi sắp tới!