Giao thoa sóng: Lý thuyết, điều kiện và công thức cần nhớ
Vật lý 11 Hiện tượng giao thoa sóng cơ
Giao thoa sóng là một hiện tượng vật lý quan trọng trong chương trình Vật lý 11, thường xuất hiện trong các đề kiểm tra và kỳ thi. Để học tốt phần này, học sinh cần nắm rõ bản chất hiện tượng, điều kiện để xảy ra giao thoa, và ghi nhớ chính xác các công thức giao thoa sóng. Bài viết này sẽ giúp bạn hệ thống đầy đủ lý thuyết giao thoa sóng, điều kiện tạo cực đại – cực tiểu, cùng các công thức Vật lý 11 dễ hiểu, dễ nhớ, giúp bạn học nhanh – hiểu sâu – làm bài hiệu quả.
I. Hiện tượng giao thoa của hai sóng trên mặt nước (xét 2 nguồn cùng pha)
1. Định nghĩa giao thoa sóng
Hiện tượng 2 sóng gặp nhau tạo nên các gợn sóng ổn định.
2. Giải thích
- Những điểm đứng yên : 2 sóng gặp nhau triệt tiêu
- Những điểm dao động rất mạnh : 2 sóng gặp nhau tăng cường
II. Phương trình giao thoa sóng tổng quát
1. Công thức tổng quát phương trình giao thoa sóng
\(x = 2a\left\lbrack \cos\frac{\pi\left(
d_{2} - d_{1} \right)}{\lambda} - \left( \frac{\alpha_{2} -
\alpha_{1}}{2} \right) \right\rbrack\cos\left\lbrack \omega t -
\pi\frac{d_{1} + d_{2}}{\lambda} + \left( \frac{\alpha_{2} +
\alpha_{1}}{2} \right) \right\rbrack\)
\(\Delta\phi = \frac{2\pi}{\lambda}\left(
d_{2} - d_{1} \right) + \left( \alpha_{1} - \alpha_{2}
\right)\)
2. Dao động của một điểm trong vùng giao thoa
\(A_{M} = 2a\left| \cos\frac{\pi(d_{2} -
d_{1})}{\lambda} \right|\)
3. Vị trí cực đại và cực tiểu giao thoa
a. Vị trí các cực đại giao thoa
\(d_{2} - d_{1} = k\lambda\)
Những điểm tại đó dao động có biên độ cực đại là những điểm mà hiệu đường đi của 2 sóng từ nguồn truyền tới bằng một số nguyên lần bước sóng λ
b. Vị trí các cực tiểu giao thoa
\(d_{2} - d_{1} = \left( k + \frac{1}{2}
\right)\lambda\)
Những điểm tại đó dao động có biên độ triệt tiêu là những điểm mà hiệu đường đi của 2 sóng từ nguồn truyền tới bằng một số nữa nguyên lần bước sóng λ
III. Phương trình giao thoa sóng
Giao thoa của hai sóng phát ra từ hai nguồn sóng kết hợp S1, S2 cách nhau một khoảng l:
Xét điểm M cách hai nguồn lần lượt d1, d2
Phương trình sóng tại 2 nguồn \(u_{1} =
Acos(2\pi ft + \varphi_{1})\) và \(u_{2} = Acos(2\pi ft + \varphi_{2})\)
Phương trình sóng tại M do hai sóng từ hai nguồn truyền tới:
\(u_{1M} = Acos(2\pi ft -
2\pi\frac{d_{1}}{\lambda} + \varphi_{1})\) và \(u_{2M} = Acos(2\pi ft - 2\pi\frac{d_{2}}{\lambda}
+ \varphi_{2})\)
Phương trình giao thoa sóng tại M: uM = u1M + u2M
\(u_{M} = 2Acos\left\lbrack \pi\frac{d_{1}
- d_{2}}{\lambda} + \frac{\Delta\varphi}{2} \right\rbrack
cos\left\lbrack 2\pi ft - \pi\frac{d_{1} + d_{2}}{\lambda} +
\frac{\varphi_{1} + \varphi_{2}}{2} \right\rbrack\)
Biên độ dao động tại M: \(A_{M} = 2A\left|
cos\left( \pi\frac{d_{1} - d_{2}}{\lambda} + \frac{\Delta\varphi}{2}
\right) \right|\) với \(\Delta\varphi =
\varphi_{1} - \varphi_{2}\)
Chú ý:
- Số cực đại: \(- \frac{l}{\lambda} +
\frac{\Delta\varphi}{2\pi} < k < + \frac{l}{\lambda} +
\frac{\Delta\varphi}{2\pi}\ \ \ \ \ (k \in Z)\)
- Số cực tiểu: \(- \frac{l}{\lambda} -
\frac{1}{2} + \frac{\Delta\varphi}{2\pi} < k < + \frac{l}{\lambda}
- \frac{1}{2} + \frac{\Delta\varphi}{2\pi}\ \ \ \ \ (k \in
Z)\)
1. Hai nguồn dao động cùng pha (\(\Delta\varphi = \varphi_{1} - \varphi_{2} =
0\))
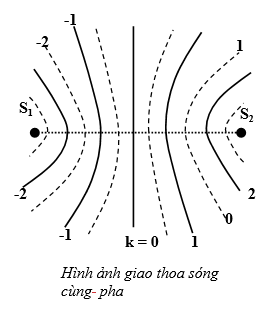
Điểm dao động cực đại: d1 – d2 = kλ (k∈Z)
Số đường hoặc số điểm (không tính hai nguồn): \(- \frac{l}{\lambda} < k <
\frac{l}{\lambda}\)
Điểm dao động cực tiểu (không dao động): d1 – d2 = (2k+1)\(\frac{\lambda}{2}\) (k∈Z)
Số đường hoặc số điểm (không tính hai nguồn): \(- \frac{l}{\lambda} - \frac{1}{2} < k <
\frac{l}{\lambda} - \frac{1}{2}\)
2. Hai nguồn dao động ngược pha (\(\Delta\varphi = \varphi_{1} - \varphi_{2} =
\pi\))
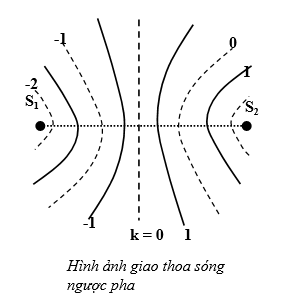
Điểm dao động cực đại: d1 – d2 = (2k+1)\(\frac{\lambda}{2}\) (k∈Z)
Số đường hoặc số điểm (không tính hai nguồn): \(- \frac{l}{\lambda} - \frac{1}{2} < k <
\frac{l}{\lambda} - \frac{1}{2}\)
Điểm dao động cực tiểu (không dao động): d1 – d2 = kλ (k∈Z)
Số đường hoặc số điểm (không tính hai nguồn): \(- \frac{l}{\lambda} < k <
\frac{l}{\lambda}\)
Chú ý: Với bài toán tìm số đường dao động cực đại và không dao động giữa hai điểm M, N cách hai nguồn lần lượt là d1M, d2M, d1N, d2N.
Đặt ∆dM = d1M - d2M ; ∆dN = d1N - d2N và giả sử ∆dM < ∆dN.
+ Hai nguồn dao động cùng pha:
- Cực đại: ∆dM < kλ < ∆dN
- Cực tiểu: ∆dM < (k+0,5)λ < ∆dN
+ Hai nguồn dao động ngược pha:
- Cực đại:∆dM < (k+0,5)λ < ∆dN
- Cực tiểu: ∆dM < kλ < ∆dN . Số giá trị nguyên của k thoả mãn các biểu thức trên là số đường cần tìm.
---------------------------------------------
Hiểu rõ hiện tượng giao thoa sóng cùng với các công thức và điều kiện quan trọng sẽ giúp bạn tự tin giải quyết nhiều dạng bài trong chương sóng cơ học lớp 11. Hãy thường xuyên ôn tập lý thuyết, luyện bài tập và ghi nhớ các công thức Vật lý 11 dễ hiểu dễ nhớ để đạt kết quả cao trong học tập. Việc nắm chắc kiến thức cơ bản là bước đệm vững chắc cho các chuyên đề nâng cao ở lớp 12 và kỳ thi THPT Quốc gia sau này.
